NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/02/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
		Quatre triangles	Heilbronn	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Équilatéral 345		Démo fallacieuse
		Sommaire de cette page >>> Démonstration fallacieuse >>> Où est le triangle isocèle ?

Le fallacieux TRIANGLE ISOCÈLE

Trouver une démonstration est grandement facilité avec l'aide d'une figure.

Sans soin, la figure peut conduire parfois à un raisonnement erroné.

Anglais: What is the flaw in this proof that all triangles are isosceles?

The art of drawing correct conclusions from incorrect pictures

Démonstration fallacieuse
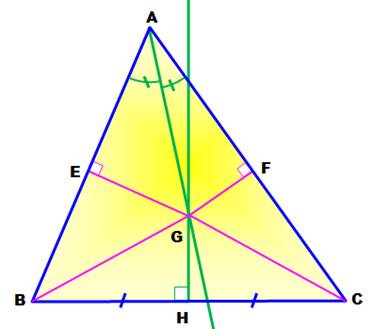
Triangle quelconque ABC. Bissectrice en A. Médiatrice de BC. Point d'intersection G. Perpendiculaires aux côtés depuis G. Propriétés de la bissectrice: GE = GF Triangles: AGE = AGF, car: Côté commun AG Angles en A sont égaux GE = GF Alors: AE = AF Propriété de la médiatrice: GB = GC Triangles: GBE = GCF, car: Angle droit en E et F GE = GF GB = GC Alors: EB = FC En sommant les deux égalités: AE + EB = AB = AF + FC = AC Le triangle ABC est isocèle !	Cette figure est fausse et elle conduit à un mauvais raisonnement, démontrant que tout triangle quelconque est isocèle. Le mystère tient au fait que le point G n'est jamais intérieur au triangle.

Où est le triangle isocèle ?
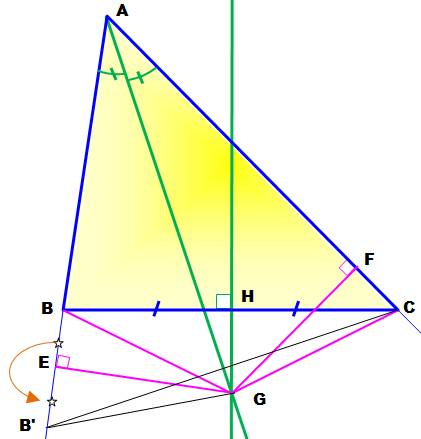
Construction Cette fois on trace soigneusement la médiatrice et, surtout, une bissectrice exacte. Quelle que soit la construction, le point d'intersection G est à l'extérieur du triangle Reprise de la démonstration On conserve les propriétés des triangles qui conduisent à: AE = AF EB = FC En ajoutant et en respectant le sens: AE + EB = AB' AF + FC = AC Le triangle AB'C est isocèle. Mais pas ABC !

Suite	Équilatéral 345 Théorème de Pythagore Démonstrations fallacieuses en algèbre
Voir	Allumettes Carrés Cercle Droite Géométrie – Index Jeux – Index Nombres triangles Polygone Relations dans les triangles Somme de r puissances k Triangle – Index
Livre	Cette démonstration fausse a été présentée par le magazine mathématique Tangente n° 184 de septembre-octobre 2018 page 40.
Site	Tous les triangles sont équilatéraux – Science étonnante Tous les triangles sont isocèles – RTS découverte Are All Triangles Isosceles? – Math Pages All triangles are equilateral – Mathematik – Avec animation
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/DemoFala.htm