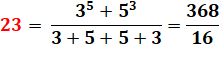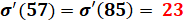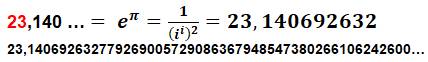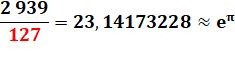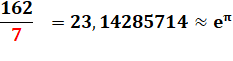|
Édition du: 06/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Maths générales du 23 |
Maths détaillées du 23 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
Géométrie Polygone à 23 côtés
(icosikaitrigone) >>> |
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales, culturelles >>>
Chiffres et numération
|
23 |
|
||||
|
23 + 2 × 3 = 29 |
|
||||
|
M(6) = 23 |
|
||||
|
23 + 32 = 55 = T10 32 – 23 = 32 |
|
||||
|
23 => 32 = 25 |
Liste: 23, 61, 163, 521, 691, 821, 1297, 1861,
4201, 4441, 4483, 5209, 5227, 9049, 9631, 12391, 14437, 16141, 16987, 61483, 63211,
65707, 67057, 92767, 94273, 96979, … |
||||
|
23 = 23 + 32
+ 2×3 23×3 + 32×2 = (3 + 2²)(33
– 23) = 133 23 + 2 = (2 + 3)² |
|
||||
|
23 => 20
+ 30 = 2 |
|
||||
|
23 => 2² + 3² = 13 |
|
||||
|
2310 = 327 |
Le
septième premier non-brésilien. |
||||
|
2310 = 2123 |
|
||||
|
23 + 32 = 55 = T10 |
|
||||
|
23 + (2×3) = 29 |
|
||||
|
23 2 + 3 = 5
& 2 x 3 = 6 |
|
||||
|
23 = 23 24 = 23 × 3 |
|
||||
|
23 => 2² = 4, 3² = 9
=> 49 = 7² |
|
||||
|
23 = (2² × 3²) – (2² + 3²) |
Unique ? Aucune
solution non triviale avec les cubes ? |
||||
Addition et soustraction
|
p(23) = 1 255 p(23,2) = 12 p(23,2) = 56 … |
|
||
|
|
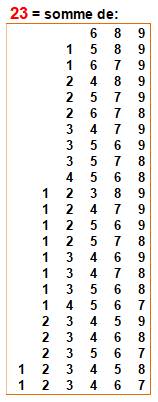
C'est la quantité maximale de partitions
avec nombres distincts de 1 à 9. Aucune somme de nombres consécutifs. |
||
|
23 + 19 + 17 + 13 + 11 + 7 + 5 + 3 + 2 = 100 |
Voir Table |
||
|
3 + 5 + 7 + … + 89 = 961 = 31² |
|
||
|
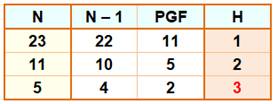
p(23) = 1 255 |
23 est le
plus grand nombre de la sorte. |
||
|
23
= 6 + 8 + 9 |
|
||
|
23
= 5 + 7 + 11 |
Remarquez
la présence des cinq plus petits premiers impairs. |
||
|
23 = 3 + 7 + 13 |
|
||
|
23 = (2 +11) + (3 +
7) |
|
||
|
2
+ 5 + … + 23 = 100 |
|
||
|
23
= 1! + 2! + 2! + 3! + 3! + 3! |
|
||
|
23
= 0×0! + 1×1! + 2×2! + 3×3! = 0 + 1 + 4 + 18 = 4! – 1 |
|
||
Multiplication, division, diviseurs
|
23 (2 et 3 sont premiers) 2 + 3 = 5 est premier 23 & 2 x 23 + 1 = 47 sont premiers 11 & 2 x 11 + 1 = 23 sont premiers |
Voir Barre
magique des nombres premiers
|
|
|
23 +
2 × 3 = 29 |
|
|
|
23
– 19 = 4 |
Record
suivant avec 97 – 89 = 8. |
|
|
17,
23, 29 |
Note: il existe un premier dans l'écart: 19.
Seul le couple 23, 29 est vraiment sexy. |
|
|
23,
67, 89, 4567 |
|
|
|
23,
29 |
|
|
|
23 x 38 = 874 = 2 + 3 +
5 + … + 23 |
|
|
|
23 2357 0,2357… 10355 |
|
|
|
23
= 3 × 23 – 1 |
||
|
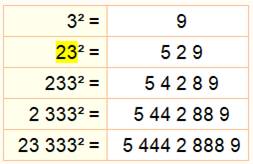
23 233 2333 23333 23333333333 23333333333333333 23333333333333333333333 |
|
|
|
23
= 4! – 1 |
||||
|
23
| (14! + 1) |
|
|||
|
|
|
|||
|
P
= 3n² + 3n + 23 |
Liste avec [n, P] [0, 23], [1, 29], [2, 41], [3, 59], [4, 83], [5, 113],
[6, 149], [7, 191], [8, 239], [9, 293], [10, 353], [11, 419], [12, 491], [13,
569], [14, 653], [15, 743], [16, 839], [17, 941], [18, 1049], [19, 1163],
[20, 1283], [21, 1409] |
|||
|
23 | 22333 |
|
|||
|
23 | 874 |
Le plus petit.
Les suivants: 53, 853, 11 869 … A045345 |
|||
|
23 | Groupe
monstre |
|
|||
|
23 = 2 mod 3 23 = 3 mod 2 |
Notez
qu'en mod 2, on a ajouté 2 pour la symétrie du motif. |
|||
|
23 = 2 333 – 2 310 23 = 9 699 713 – 9 699
690 |
|
|||
|
|
|
|||
|
|
|
|||
|
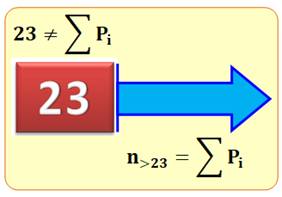
23 ≠ 2a٠3b
+ 2c٠3d |
|
|||
Avec les puissances
|
|
Exemples 22 = 1 + 4
+ 8 + 9 23 =
IMPOSSIBLE 24 = 8 +
16 25 = 25 |
||
|
23 =
1² + 2² + 3² + 3² |
|
||
|
23
= 12² – 11² = 12 + 11 |
|
||
|
23 =
33 – 2²
=
27 – 4 |
Différence
entre un cube et un carré. |
||
|
23
= 25 – 32 = 211 – 452 = 33 –
22 |
Notez les
mêmes chiffres dans le troisième cas. |
||
|
23
= 2 · 23 + 7 · 13 = 23 + 23 + 13
+ 13 + 13 + 13 + 13
+ 13 + 13 23 = 33 + 6 · (–1)3 |
Tout entier est décomposable
en somme d'au plus neuf cubes. En fait, les deux seuls qui nécessitent les 9
termes sont 23 et 239. Prouvé par
Dickson en 1939.
Voir
Somme
de puissances: Théorème de Waring |
||
|
|
|
||
|
23
= 05 + 14 + 23 + 32 + 41
+ 50 |
|
||
|
|
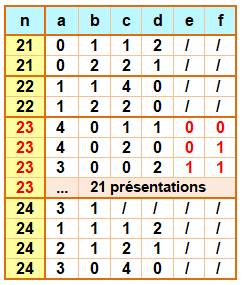
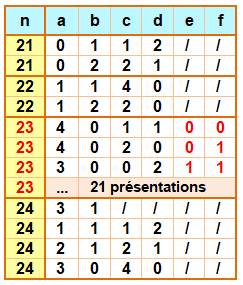
23 = 24٠30 +
21٠31 + 20٠30
= 16 + 6 + 1 Ce nombre exige trois termes. Et dans ce cas, il existe
21 possibilités dont trois présentées dans le tableau. Voir Nombres
lisses |
||
|
233
= 12 167 23 =
(2x3) + (1+2+1+6+7) |
|
|
|||||
|
23²
= 529 |
|
||||||
|
23²
= 529 27²
= 729 |
|
||||||
|
23²
= 529 841 = 29² |
|
||||||
|
23² =
265² – 264² |
|||||||
|
233 + 1 = 12 168 = 23 x 32 x 132 |
|
||||||
|
235
= 6 436 343 & 6+4+3+6+3+4+3 = 29 295 = 20 511 149
& 2+0+5+1+1+1+4+9 = 23 |
|
||||||
|
223
= 8 388
608 |
|
||||||
|
23! =
25 852 016 738 |
Seul cas pour
un nombre premier.
|
|
||
|
23
= 4! – 1 23 =
1x1! + 2x2! + 3x3! |
|
|
||
|
23
|
||||
|
23
et 32 46
et 64 |
|
|||
|
R23 = 111…1123 fois |
|
|||
|
|
|
|||
Dénombrement, jeux et curiosités
|
23 (50%) |
|
||
|
23 = 3 × 7 + 2 23 = 5 × 4 + 3 23 = 7 × 3 + 2 |
nombre
avec reste 2 lorsque divisé par 3; Solutions:
23 + 105k. |
||
|
23, 15, 6, Cycle: 23, 70,
35, 106, 53, 160, 80, 40, 20, 10, 5, 16,
8, 4, 2, 1 |
|
||
|
23
|
|
||
|
|
|
||
|
23 nombres
|
|
||
|
23 tiges |
Une
autre source
donne 36. |
||
|
1, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159, … |
|
||
|
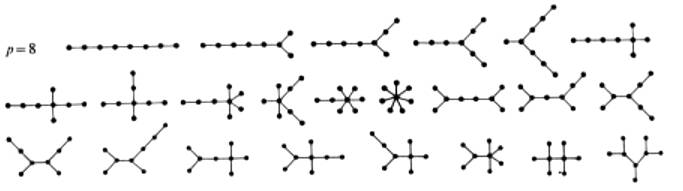
Les vingt-trois arbres à huit sommets
Source image: nothinisreal |
|||
|
|
Voir Motif
/ Repdigit
/ Répétition
de motifs
/ |
|
|
|
|
23!
= 25 852 016 738 884 976 640 000 |
|
|
23,04428… = 1/9 + 1/19 + … |
|
|
|
|
Valeur
avec 50 décimales. |
|
|
22,459
… 23,140
… |
Voir Suite |
|
|
23,141592… = 20 + π |
|
|
|
|
|
|
|
|
|
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 1, 1] 3, [2, 1, 2] 4,
[1, 1, 3] 5, [4, 3] 6,
[3, 5] 7, [3, 2] anagramme 8,
[2, 7] 9,
[2, 5] |
10,
[2, 3] 11, [2, 1] 12,
[1, 11] 13,
[1, 10] 14,
[1, 9] 15,
[1, 8] 16,
[1, 7] |
17,
[1, 6] 18,
[1, 5] 19,
[1, 4] 20,
[1, 3] 21,
[1, 2] 22,
[1, 1] 23,
[1, 0] |
22,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Site |
|
|
Cette
page |
![]()