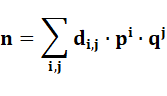|
Édition du: 02/12/2023 |
|
INDEX Facteurs et exposants
spéciaux |
Types de Nombres – Diviseurs |
|||
|
Semi-parfaits (SP) |
||||
![]()
|
Nombres DOUBLE-BASE
Nombres formés de la somme de
produits n'ayant pour facteurs que les nombres 2 et 3; ou, plus généralement,
deux nombres premiers p et q.
|
||
|
|
Sommaire de cette page >>> Système double-base >>> Types de
représentations >>> Historique et intérêt
>>> Le cas du nombre 10 –
Exemple >>> Nombres représentés
par 1 à 3 termes |
Débutants Glossaire |
Anglais: Double-Base Number System (DBNS), (p,
q)-ary partitions
|
Nombres double-bases avec 2 et 3 Nombre
de la forme: |
Exemple 4 116 = 22٠31
+ 23٠33 + 24٠35 |
||
|
Partition Il
s'agit d'une partition
particulière des nombres, dite {2, 3}-partition Chaque
terme est appelé: entier {2, 3} ou {2, 3}-integer en anglais (aussi: the
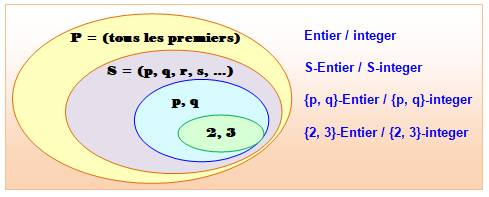
twothree numbers). Nombres double-base (en général) Avec
{p, q}, p et q étant deux nombres premiers, le système est dit à base-double.
Alors: Il
existe une version avec d prenant les valeurs 1 ou -1. |
Représentation de 4 116
|
||
|
Types de nombres selon les facteurs employés Place
des nombres à double-base dans le monde des entiers. En
représentation s, les nombres utilisés sont généralement des s plus petits
nombres premiers. |
|
||
|
Redondance Avec
ce système à base double, l'unicité de la représentation
d'un nombre n'est pas garantie, contrairement au système à base simple. Évidemment,
tout nombre est représenté par ce système. En effet, la somme de n fois 20٠30 = 1 représente toujours le nombre n. Forme canonique La
forme ayant le moins de termes est dite canonique.
Il peut y en avoir plusieurs. Il
s'agit de trouver le plus grand nombre 2a٠3b qui
est inférieur à n, le nombre à représenter. Ce qui revient à trouver: La
recherche de ces formes pour de grands nombres est extrêmement compliquée |
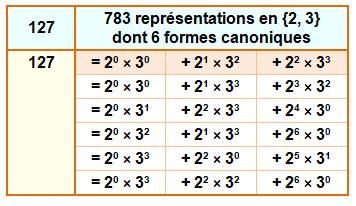
Exemple de forme canonique
La
première ligne avec 127 = 1 +
18 + 108 est celle ayant le plus grand terme (108); on pourrait dire qu'elle
représente la forme canonique principale. |
|
|
Le système de numérotation Double-Base (DBNS),
introduit en 1999 par V. Dimitrov et
G. A. Jullien, présente des avantages dans de nombreuses applications, comme la
cryptographie et le traitement
du signal numérique. Récemment, dans le cadre de son doctorat, R. Muscedere
a proposé des solutions pour les opérations difficiles avec le système de
nombre à logarithme multidimensionnel
(MDLNS), qui peut être considéré comme une généralisation du DBNS. Il aborde les problèmes des additions,
soustractions et conversions à partir du binaire. Des méthodes
efficaces ont été proposées – utilisant des tables de recherche avec schéma
d'adressage spécifique - pour les applications de traitement du signal
numérique, où la plage dynamique des nombres ne dépasse généralement pas 16 à
32 bits. Cependant, de telles solutions basées sur des
tables deviennent irréalistes à mettre en œuvre à mesure que les chiffres
augmentent, comme pour les applications cryptographiques par exemple, et
semblent également assez difficiles à généraliser. |
Intérêt
|
Ce système à double base facilite grandement le
calcul des additions, soustractions et multiplications par informatique, car
diminuant le nombre de fonctions logiques pour les réaliser (gate count). Ce
système est bien adapté au traitement de signal et autres applications
similaires. Inconvénients: la conversion aller et retour du
système décimale classique à ce système double base. |
|
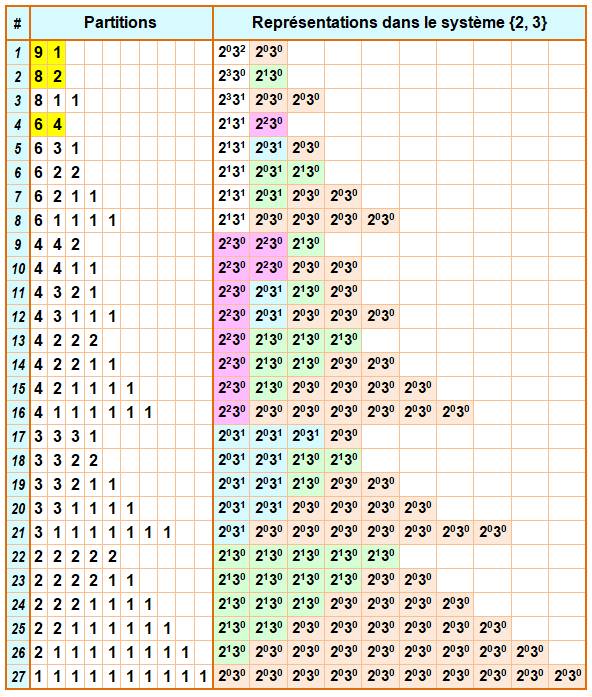
Représentations de {2, 3}-10 Le nombre
10 comporte vingt-sept représentations en
système {1, 2} dont trois canoniques (en
jaune sur le tableau). Il y en a
seulement sept si on retire toutes celles
en 20٠30 = 1. |
Possibilités Valeurs
de 2k ≤ 10 : (1, 2, 4, 8) Valeurs
de 3k ≤ 10 : (1, 3, 9) Valeurs
des produits ≤ 10: (1, 2, 4, 8, 3, 6, 9) Méthode Il
s'agit de trouver les partitions de 10 faites de ces nombres. On
commence par le plus grand nombre 9 auquel il faut ajouter 1. Idem
pour 8 avec le complément 2, lequel peut à nouveau être décomposé en 1 + 1 ;
soit deux représentations. Etc. |
|
|
Les 27 représentations de 10
Exemple: 10 = 9 + 1 = 20٠32 + 20٠30
|
||
|
Nombres représentés
par 1 à 3 termes jusqu'à 500 |
||
|
1 terme (33) Ex: 432 = 2433 486 = 2135 |
Nombre 3-friables 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27,
32, 36, 48, 54, 64, 72, 81, 96, 108, 128, 144, 162, 192, 216, 243, 256, 288,
324, 384, 432, 486 Le nombre 5 est le plus petit manquants.
Ensuite ils sont évidemment très nombreux. Voir Nombres
3-friables Voir OEIS A003586
– 3-smooth numbers |
|
|
2 termes (285) Ex: 498 |
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,
15, 16, 17, 18, 19, 20, 21, 22, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 48, 49, 50, 51, 52, 54, 55, 56,
57, 58, 59, 60, 62, 63, 64, 65, 66, 67, 68, 70, 72, 73, 74, 75, 76, 78, 80,
81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 93, 96, 97, 98, 99, 100, 102,
104, 105, 108, 109, 110, 111, 112, 113, 114, 116, 117, 118, 120, 123, 124,
126, 128, 129, 130, 131, 132, 134, 135, 136, 137, 140, 144, 145, 146, 147,
148, 150, 152, 153, 155, 156, 160, 162, 163, 164, 165, 166, 168, 170, 171,
172, 174, 176, 177, 178, 180, 182, 186, 189, 192, 193, 194, 195, 196, 198,
200, 201, 204, 208, 209, 210, 216, 217, 218, 219, 220, 222, 224, 225, 226,
228, 232, 234, 236, 240, 243, 244, 245, 246, 247, 248, 249, 251, 252, 255,
256, 257, 258, 259, 260, 261, 262, 264, 265, 267, 268, 270, 272, 273, 274,
275, 279, 280, 283, 288, 289, 290, 291, 292, 294, 296, 297, 300, 304, 306,
307, 310, 312, 315, 320, 324, 325, 326, 327, 328, 330, 332, 333, 336, 337, 339,
340, 342, 344, 348, 351, 352, 354, 356, 360, 364, 369, 371, 372, 378, 384,
385, 386, 387, 388, 390, 392, 393, 396, 400, 402, 405, 408, 411, 416, 418,
420, 432, 433, 434, 435, 436, 438, 440, 441, 444, 448, 450, 452, 456, 459,
464, 465, 468, 472, 480, 486, 487, 488, 489, 490, 492, 494, 495, 496, 498,
499 Les
manquants jusqu'à 101: 23, 46, 47,
53, 61, 69, 71, 77, 79, 92, 94, 95, 101. Pour information, une des représentations
des 22 plus petits:
|
|
|
3 termes (498) Ex: 500 |
TOUS, sauf: 431 jusqu'à 500 et TOUS sauf: 431, 485, 509, 565, 637, 671,
719, 725, 727, 862, 887, 935, 941, 943, 959, 967, 970 jusqu'à 1000 |
|
|
Records |
Plus petits nombres non représentés par k
termes en 2a 3b. 1, 5, 23, 431, 18 431, 3 448 733, 1 441 896 119 OEIS
A018899 5, 23, 431 et 1 441 896 119 sont des
nombres premiers. 18 431 = 7 × 2633 3 448 733 = 37 ×
83 ×
1123 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette
page |
http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Doblebas.htm
|