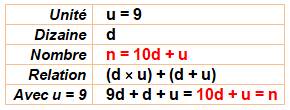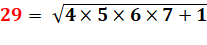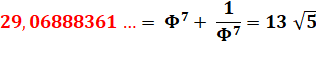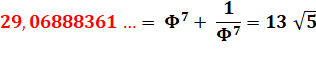nombre vingt neuf, maths

Édition du: 01/02/2025

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	20	21		22	23		24	25	26	27	28	29

Nombre 29

Maths générales du 29

Maths détaillées du 29

Lune

Vingt-neuf

Twenty-nine

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1101
Bases	131₄ 45₆
Romain	XX IX

Suite

29 = 2² + 3² + 4²

Caractérisation du nombre

Congruent

Coster

Curzon

Déficient

Facteur carré (sans)

Gilda

Glissant

Hofstadter – NON

Impair

Lucas

Markov (2, 5, 29); (2, 29, 169); …

Pell

Perrin (12^e)

Premier bon

Premier de Chen

Premier de Pythagore

Premier de Ramanujan

Premier de Sophie Germain

Premier fort

Premier jumeau avec 31

Premier long

Premier primorielle (5# – 1)

Premier régulier

Premier résistant

Premier supersingulier

Queneau

Tarte ou pizza (7 coupes)

Tétrabonacci

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Chiffres et numération

29	N'est repdigit dans aucune base. Il n'est pas brésilien.
29 + 92 = 121 = 11² 29 – (9 × 2) = 11		Devient palindrome et carré en lui ajoutant son retourné. Le plus petit. Suivants 38, 47, 56, 65, 74, 83, 92 avec la même somme 121. Ils sont 214 jusqu'à 1000. Table >>>
29 = (2x9) + (2+9)		Nombre égal à produit des chiffres + somme des chiffres, comme tous les nombres à deux chiffres terminés par 9.
2⁹ + 9² = 593		Opération avec ses chiffres qui produit un nombre premier.

Addition et soustraction

p(29) = 4 565	Quantité de partitions du nombre.
29 = 5 + 7 + 8 + 9 = 1 + 2 + 3 + 4 + 5 + 6 + 8	Partition unique avec quatre chiffres différents. Partition unique avec sept chiffres différents.
	Motif général (exemple) de somme de consécutifs sur somme de consécutifs.
29 = (1+1) + (1+3) + (1+7) + (1+9) + (2+3)	Somme des chiffres des premiers à deux chiffres inférieurs à 29.
			Nombre glissant.
1+1+2+3+5+8+13+21+34+ 55+89+144+233+377 = 986 = 29 x 34		La somme de 14 nombres de Fibonacci consécutif est divisible par 29

Multiplication, division, diviseurs

29 = 1 x 29	10^e Nombre premier 100^e = 541 1000^e = 7 919
29 et 31	Cinquième paire de premiers jumeaux.
29 > (23 + 31) / 2	Premier fort (3^e).
29 & 2 x 29 + 1 = 59 sont premiers	Nombre premier de Sophie Germain (p et 2p + 1 sont premiers).
[2, 5], [4, 11], [6, 29], [8, 97],	Plus petits nombres premiers avec écart croissant par rapport au premier précédent.
2n² + 29_{n = 0 à 28}	Tous ces nombres sont premiers.
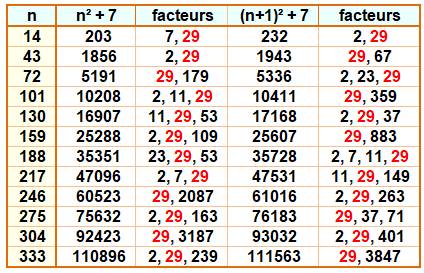
k \| (n² + 7) & (n + 1)² + 7 alors k = 29	Si un nombre divise à la fois ces deux expressions, alors ce nombre est 29. Exemples ci-dessous.
29 = (2 × 7) + (3 × 5) = (5 × 7) – (2 × 3)	Avec les quatre plus petits nombres premiers.

Exemples

Voir Brève 47-932 / Nombre 5 pour propriété identique

28 = 2² × 7 29 30 = 2 × 3 × 5	Tous les nombres inférieurs à 29 ont au plus deux facteurs distincts.
29 = Plancher(1,52469996…^{2^3})	Ex: n = 3, cette constante à la puissance 8 donne 29, le premier juste supérieur à 5². Liste: 2, 5, 29, 853, 727613, 529420677791, … OEIS A059784
29 => abs(2 – 9) = 7, 2 + 9 = 11, 7 + 11 = 18, 11 + 18 = 29	Nombre de Gilda, le plus petit.
	Deux antécédents aliquotes.
Cf. 30 = 2 x 3x 5	Plus petit premier dont le successeur a trois facteurs uniques.
	Le cumul de la somme des inverses des diviseurs des nombres jusqu'à 29 passe le seuil du nombre entier 3.
29 \| Groupe monstre	Premier supersingulier. Il divise le groupe monstre.

Avec les puissances

29 = 2² + 5² = 2² + 3² + 4²	Nombre binomial. Somme des carrés de nombres consécutifs Première somme de trois carrés consécutifs égale à un nombre premier. Seules deux sommes de jusqu'à quatre carrés. Voir Autour de 1 2 3 4 5
29 = 1³ + 1³ + 3³	Somme de cubes.
29 = 2² + 3² + 4²	Somme de trois carrés consécutifs.
29 = 2⁵ – 3¹	Nombre en 2^a – 3^b.
29 = 15² – 14² = 15 + 14	Différence de deux carrés. Motif général.
	Le produit de quatre nombres consécutifs plus 1 est un carré.

En puissance

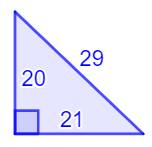
29² = 20² + 21² = 400 + 441 = 841	9^e triplet de Pythagore primitif. Deuxième plus petit carré somme de deux carrés consécutifs. Le plus petit étant 5² = 4² + 3².
29² = 20² + 21² = 841	Somme de carrés de nombres consécutifs.
29³ = 24 389 2×4×3×8×9 = 1728 = 12³		Produit des chiffres du cube est un cube.
29³ = 65² + 142² = 58² + 145²		Cube somme de deux carrés.
29² = 4 × 5 × 6 × 7 + 1 = 841		Produit de quatre nombres consécutifs plus 1 (toujours un carré)
23⁵ = 6 436 343 & 6+4+3+6+3+4+3 = 29 29⁵ = 20 511 149 & 2+0+5+1+1+1+4+9 = 23			Motif en couple.
2²⁹ – 1 = 233 x 1103 x 2089 = 536870911		Nombre de Mersenne avec exposant premier. Le plus petit comportant trois facteurs.
29⁵ x 5 = 102 555 745		Super 5 nombre. Le plus petit en 5.
2²⁹ = 536 870 912 => 53 791 est premier		Tous les chiffres une fois sauf le "4". La suite des chiffres impairs forme un nombre premier.
2²⁹ = 536 870 912 => 12 356 789		Le nombre formé par les chiffres rangés par ordre croissant est un nombre premier.

Dénombrement, jeux et curiosités

29 cases maximum		Pour le parcours du fou aux échecs.
		Jeu du quatre 4.
			Avec quatre 6.
29 = 2 + 4 + 8 + 15		Nombre tétrabonacci.
29 = ½ (7 x 8) + 1	Nombre tarte: quantité maximale de parts de tarte obtenue en la coupant avec 7 coups de couteau.

Géométrie

29 régions créées par les côtés prolongés de l'heptagone.

>>>

Autour du nombre

Nombre premier long. La période du développement décimal de la fraction est maximale en une seule suite permutée pour toutes les fractions avec ce dénominateur.
F₂₉ = 514 229	Le 29^e Fibonacci est un nombre premier qui se termine par 29.
7² + 8² + … + 29² = 8 464 = 92²	Carré somme de carrés.
29! = 8 841 761 993 739 701 954 543 616 000 000		Plus petite factorielle sans chiffre unique