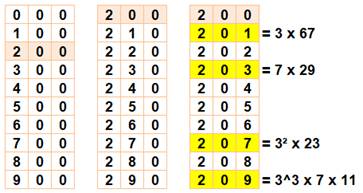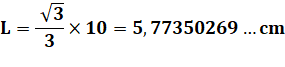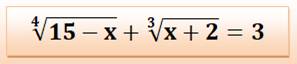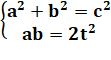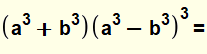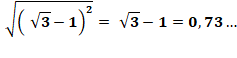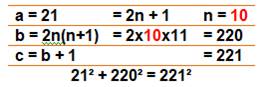NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 37

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

720. Médianes du triangle
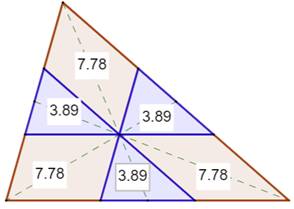
Construction Un triangle. Ses médianes (pointillés verts) qui se coupent en un point G (le centre de gravité). Les parallèles aux côtés passant par G. Propriétés Les triangles bleus ont tous la même aire, de même que tous les parallélogrammes ocres. Les trapèzes formés par deux ocres et un bleu ont la même aire. De même que les triangles avec deux bleus et un ocre.
Brèves associées	>>> Bissection du triangle		>>> Brèves Construction – Index
Pour en savoir plus	>>> Médianes et partage du triangle		>>> Triangles – Index

721. Jamais PREMIER ou composé stable
Formation des nombres À partir d'un nombre –racine (ici 326), chacun des chiffres est modifié pour former 3 x 10 = 30 nombres (Voir tableau). En fait, 28 car la racine est répétée trois fois. Nature des nombres La probabilité de trouver des nombres premiers parmi ces 28 nombres est grande. Pourtant, il existe des nombres-racines pour lesquels aucun nombre n'est premier. C'est le cas pour cet exemple avec 326. Plus petit Le plus petit de ces nombres jamais premier par modification est 200. Le sort des deux colonnes de gauche est vite réglé. Ce sont tous des nombres divisibles par 10. Sur la colonne de droite, en éliminant les nombres divisible par 2, restent quatre nombres dont trois sont vite identifiés comme divisibles par 3; le dernier est divisible par 7. Conclusion: tous ces nombres sont composés.		Nombre 326 Nombre 200
Brèves associées	>>> Nombres premiers résistants		>>> Brèves Type de nombres – Index
Pour en savoir plus	>>> Jamais-premier par modification		>>> Nombres composés

722. Tangente à deux cercles
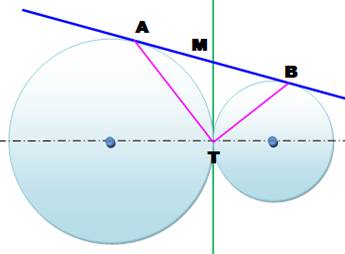
Problème Deux cercles tangents. Une droite tangente aux deux cercles. Le triangle ABT avec les points de tangence pour sommets. Quelle est la valeur de l'angle ATB ? Solution Les segments de tangente à un cercle, issue d'un même point, sont égaux. (isométriques). MA = MT = MB Si M est le centre d'un cercle de rayon MA, alors B et T sont sur ce cercle. AB est le diamètre et le triangle ABT, inscrit dans le demi-cercle, est rectangle en T.
Brèves associées	>>> Deux cercles tangents		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème des angles alternés		>>> Cercles – Index

723. Taille du triangle isocèle
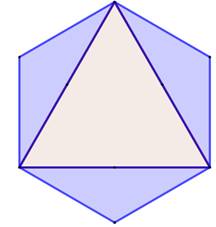
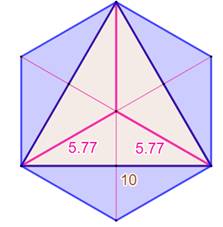
Problème Un triangle équilatéral de côté 10 cm. Trois triangles isocèles identiques dont la somme des aires est égale à celle du triangle équilatéral. Quelle est la longueur du côté du triangle isocèle ? Solution On commence par flanquer les triangles isocèles avec leur base sur les côtés du triangle équilatéral. Puis, on dessine les symétriques par rapport aux droites supportant les côtés du triangle équilatéral. Si la somme des trois aires est égale à celle du triangle équilatéral, c'est que les trois triangles isocèles se réunissent au centre de gravité. La longueur du côté est alors: La figure forme un hexagone régulier.
Brèves associées	>>> Hexagone et triangles		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle équilatéral >>> Triangle isocèle		>>> Hexagone >>> Centre de gravité du triangle

724. Aire mystère du pentagone
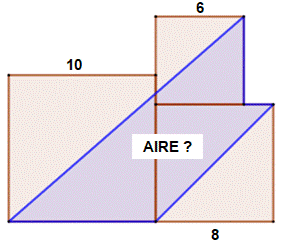
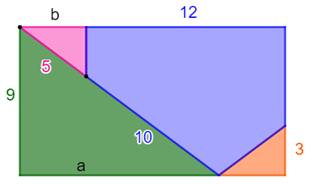
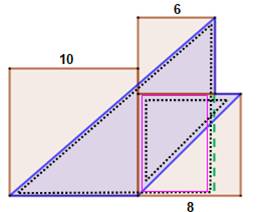
Énigme avec ces trois carrés Calculer l'aire de la zone bleue.		Solution Dessiner le trait pointillé vert. Grand triangle: (10 + 6) ( 10 + 6 – 2) / 2 = 112 Rectangle rose à retirer: 6 x 8 = 48 Petit triangle à ajouter: 8 x 8 / 2 = 32 Aire du pentagone bleu: 112 – 48 + 32 = 96
Brèves associées	>>> Aire mystère du triangle		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Aires		>>> Énigmes – Index

725. Calcul avec des logarithmes
Une expression en log pour x (x = logarithme de 2 en base 12) et une autre pour y (y = logarithme de 72 en base 6). Comment exprimer y en fonction de x ? D'abord effectuer un changement de base.
Brèves associées	>>> Logarithme		>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Calculs avec les logarithmes		>>> Logaritmes – Bases

726. Calcul avec des racines
Cette équation semble impossible à résoudre. Voici une piste. Voir le lien pour la solution algébrique.		Solution immédiate (avec l'intuition que 2 + 1 = 3)
Brèves associées	>>> Calcul avec racines carrées		>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Solution complète de cette équation		>>> Division des ponynômes

727. Énigme de l'échelle et du mur
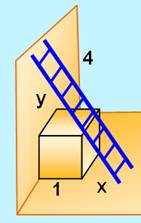
Énigme Une échelle de 4 m est appliquée à un mur. Elle s'appuie sur un cube de 1m de côté. Quelles sont les longueurs x et y ? Solution Après calcul, on montre que: x = 0,362… et y = 2,7609… L'énigme semble simple et pourtant elle requiert de l'astuce pour la résoudre !
Brèves associées	>>> Énigme du parking	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Solution complète de cette énigme	>>> Deux échelles

728. Paradoxe de la corde soulevée
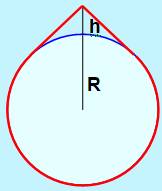
Énigme Une corde est enrouée autour du cercle. Son périmètre est allongé d'une petite longueur E. La corde est maintenue tendue par un poteau de hauteur h. Quelle est la longueur de ce poteau ? Solution Le calcul de la solution fait appel à la trigonométrie et produit ce résultat pour h très petit par rapport à R: Exemple: Cas de la Terre avec E = 1 m, alors h atteint plus de 121 m.		Rayon de la Terre: 6 378 125 m
Brèves associées	>>> Paradoxe de la corde tendue	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Calcul complet pour ce paradoxe	>>> Tangente >>> Terre

729. Triangles de Pythagore
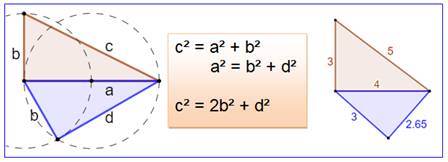
Triangle rectangle de Pythagore Ce sont les triangles dont les côtés sont des nombres entiers, autrement-dit, les trois nombres forment un triplet de Pythagore. Ils sont nombreux; une infinité. Particuliers Double: 25² = 7² + 24² = 15² + 20² Quadruple: 65² = 16² + 63² = 25² + 60² = 33² + 66² = 39² + 69²			Théorème de Fermat L'aire ces triangles rectangles en nombres entiers n'est jamais un nombre carré. Ce qui veut dire que ce système d'équations n'a pas de solution:
Une conséquence du théorème La configuration des deux triangles rectangles de cette figure est impossible à résoudre en nombres entiers. À droite, un exemple de calcul avec le plus petit et le plus célèbre, des triangles de Pythagore.
Brèves associées	>>> Triplets de Pythagore: a² + b² = c² >>> Triplets de Pythagore – Divisibilité			>>> Triangle {3, 4, 5} >>> Brèves Opérations – Index
Pour en savoir plus	>>> Triangle de Pythagore			>>> Triplets de Pythagore

730. Carrés et concaténation
Il existe une grande variété de motifs faisant intervenir la concaténation et les carrés. Par exemple: 12² = 144 20² = 200 144 200 = 380² Ou encore 4 et 9 sont des carrés et 49 l'est aussi.		Les chiffres des deux nombres se retrouvent dans la somme de leurs carrés. Quatre formes possibles:
Brèves associées	>>> Carrés, nombre et de son retourné		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Carrés et concaténation		>>> Nombres à motifs – Index

731. Énigme des deux cercles
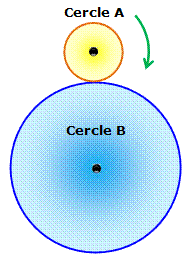
Énigme Deux cercles de rayon R et 3R. Le petit tourne sur le grand sans glissement. Après rotation, il retrouve sa position de départ. Combien de tours a-t-il effectué ? Indice Non ! ce n'est pas trois tours … C'est la réponse habituelle, mais elle est erronée. Solution Pour parcourir la circonférence bleue, le cercle jaune doit faire trois tours. C'est vrai. Mais, pendant ce temps, la pièce roule sans glisser. Elle est donc en rotation et fait un tour sur lui-même. La solution: quatre tours.
Brèves associées	>>> Énigme des 30 euros	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigme de la pièce qui roule	>>> Théorème d'al-Tûsi

732. Les cubes d'argent de Dudeney
Puzzle Henry Ernest Dudeney (1857-1930), célèbre pour ces énigmes, propose de trouver les dimensions de deux cubes d'argent dont le volume total est 17 cm^3. Autrement-dit, il faut trouver une paire de nombres rationnels (des fractions) tels que la somme de leur cube soit 17. Dudeney prévient que ce sera très dur. Recherche La recherche des nombres sommes de deux cubes rationnels peut être effectuée par programmation. Il faut un ordinateur puissant. Ou alors, en utilisant des identités telles que, connaissant une solution, on en déduit d'autres. C'est le cas avec l'identité de Fermat.		Somme de deux cubes rationnels pour 17 Identité de Fermat
Brèves associées	>>> Somme de trois nombres = 30		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Sommes de deux cubes rationnels		>>> Théorème d'al-Tûsi

733. Irrationnel ?
On trouve ce genre de question sur Internet: est-ce que cette expression avec des radicaux est irrationnelle ou non ?		Pour calculer ce type d'expression, il faut se souvenir de l'identité remarquable (a + b)² = a² + 2ab + b² et l'appliquer à des formes avec radicaux. Voyez cet exemple où les nombres entiers s'ajoutent en masque le carré.
Pour les experts, notez que le radical indique que l'on sélectionne la racine carrée positive.
Brèves associées	>>> Racine cubique – Calcul mental		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Racine carrée >>> Calculs avec des radicaux		>>> Viral sur Internet

734. Rectangle en carré
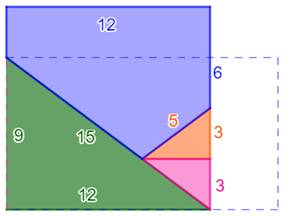
Problème Quel est le périmètre du carré que l'on peut former avec ces quatre pièces ? Solution On va montrer que la longueur du rectangle est 16. Son aire sera donc 9 x 16 = 144 = 12². Et le côté du carré sera 12. Longueur du rectangle Dans le triangle vert, le troisième côté: a² = (10 + 5)² – 9² = 225 – 81 = 144 = 12² Triangles semblables Longueur du rectangle L = 4 + 12 = 16		Figure initiale du rectangle Figure finale du carré
Brèves associées	>>> Rectangle dans carré – Aire		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Rectangle		>>> Carrés – Index

735. Triplets jumeaux de Pythagore
Observations Les triplets de Pythagore sont de la forme: a² + b² = c². Ils sont jumeaux si c = b + 1. Formule Tous les nombres impairs (a = 2n + 1) sont à l'origine d'un triplet. Il existe une formule toute simple pour les trouver: ; ; Trouver b et c pour a = 21 Ou plus directement : b = 1/2 (a² – 1) = 440/2 = 220		Triplets jumeaux (les cinq plus petits) Propriété remarquable a² = c² – b² = c + b 5² = 13² – 12² = 13 + 12 7² = 25² – 24² = 25 + 24
Brèves associées	>>> Triplets de Pythagore – Divisibilité		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Triplets jumeaux de Pythagore		>>> Triplets

736. Bissectrice de l'angle droit
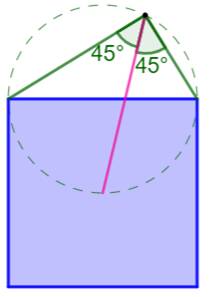
Problème Comment construire la bissectrice d'un angle droit ? Construction Construire un triangle rectangle, avec une hypoténuse quelconque. Dessiner le carré sur cette hypoténuse. Trouver le centre du carré à l'aide des deux diagonales. Joindre ce point au sommet de l'angle droit (segment rose). C'est la bissectrice e l'angle droit Démonstration Elle est simple dès que l'on a construit le cercle vert.
Brèves associées	>>> Carré passant par quatre points		>>> Brèves Constructions – Index
Pour en savoir plus	>>> Carre, triangle et bissectrice		>>> Bissectrices

737. Triangle Napoléon
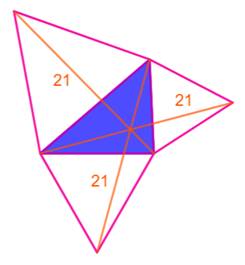
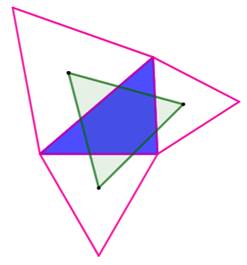
Un triangle quelconque (bleu). Les trois triangles équilatéraux externes sur les côtés. Les segments joignant un sommet "équilatéral" au sommet opposé du triangle quelconque sont de même longueur (ici 21). Le triangle (vert) dont les sommets sont les centres des triangles équilatéraux est un triangle équilatéral.
Brèves associées	>>> Triangles – Types		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle Napoléon		>>> Triangles – Index

738. Énigme n°12 d'Alcuin (735-804)
Propositiones ad acuendos iuvenes – Alcuin( vers 800)
Propositions (ou énigmes) d'Alcuin pour affuter l'esprit des jeunes		Propositions (or problems) by Alcuin to sharpen the young
Proposition à propos d'un père de famille et de ses trois fils. À sa mort, un père laisse à ses trois fils 30 cruches de verre dont 10 étaient pleines d’huile; dix autres étaient remplies à moitié; et, les dix dernières étaient vides. Qui peut partager l’huile et les cruches de façon que chacun des trois fils reçoive le même nombre de cruches et la même quantité d’huile ? Solution Il y a trois fils et 30 cruches. De celles-ci, 10 sont pleines, 10 à moitié pleines et 10 vides. Avec trois fois dix cruches qui font 30, chaque fils doit recevoir 10 cruches. Faisons les parts. Soit, au premier fils, on donne 10 cruches à moitié vides ; au deuxième, 5 cruches pleines et 5 vides ; au troisième, comme pour le second, 5 cruches pleines et 5 vides. Alors, le partage sera le même tant en huile qu’en cruches.		Proposition concerning a certain father and his three sons. A certain father died and left as an inheritance to his three sons 30 glass flasks, of which 10 were full of oil; another 10 were half full, while another 10 were empty. Let him divide, he who can, the oil and flasks so that an equal share of the commodities should equally come down to the three sons, both of oil and glass. Solution There are three sons and 30 glass flasks. However, of the flasks, 10 are full, 10 half full, and 10 empty. Take three times 10, which makes 30, so each son shall receive 10 flasks as his portion. Divide up the three portions, that is, give to the first son 10 half flasks, to the second son five full and five empty. Do the same for the third son, and the brothers' portions of glass and oil shall be the same.
Brèves associées	>>> Château et douves		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Triangles entiers et partition en trois		>>> Alcuin

Voir Autres propositions d'Alcuin sur Récréomath ou sur Mac Tutor

739. Arrondi, planche et plafond
Manière de rendre l'approximation d'un nombre pour en réduire la quantité de décimales. ARRONDI: nombre le plus proche avec la quantité de décimales désirée. Ex: 3, 333… => 3. PLANCHER: nombre sans les décimales superflues. Ex: 3, 333… => 3. PLAFOND: nombre plancher plus 1 sur la dernière décimale. Ex: 3,333… => 4.		Bon à savoir pour un résultat en nombres entiers
Brèves associées	>>> Chiffres et nombres		>>> Brèves Numération – Index
Pour en savoir plus	>>> Arrondi, plancher, plafond		>>> Numération – Index

Retour	Brèves de maths – Page 36
Suite	Brèves de maths – Page 38
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve37.htm