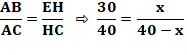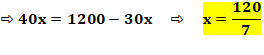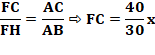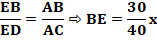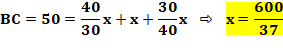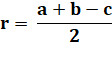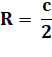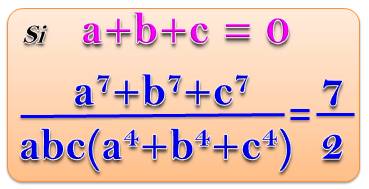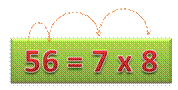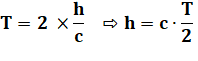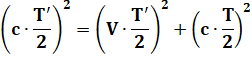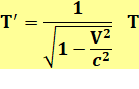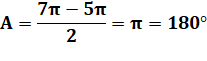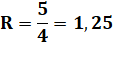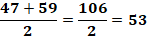NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 36

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

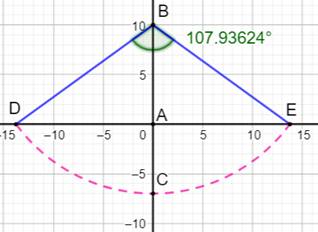
700. Pentagone approché
Construction approchée particulièrement simple à réaliser avec une règle graduée et un compas. Construction Sur l'axe vertical marquer B en (0, 10) et C en (0, -7) Cercle (B, BC). Intersection en D et E avec la droite horizontale en A. L'angle DBE est pratiquement celui du pentagone régulier à 0,6 pour mille près.
Brèves associées	>>> Pentagone de l'arpenteur		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Constructions approchées du pentagone		>>> Mesures dans le pentagone

701. Nombre 16
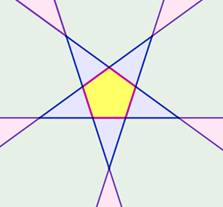
Puissance de 2 et de 4 16 = 2 x 2 x 2 x 2 = 2^4 (1000 en binaire) = 4 x 4 = 4^2 = 2^2 x 2^2 Nombre faute de frappe 16 = 2^4 et 16 = 24 en base 6 (16 = 2 x 6 + 4) Deux nombre successifs qui produisent des palindromes: 16 + 17 = 33 16 x 17 = 272 16² + 17² = 545		Un pentagone dont les côtés sont prolongés découpe le plan en seize régions
Brèves associées	>>> Nombre 15		>>> Brèves Nombres – Index
Pour en savoir plus	>>> DicoNombre 16 – Maths >>> DicoNombre 16 – Culture		>>> Palindromes >>> Polygones et régions

702. Figure du moulin à vent
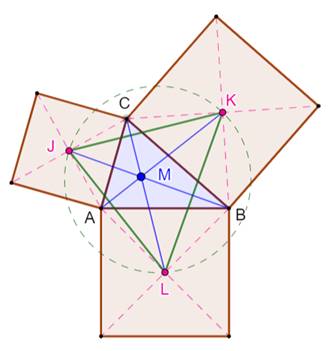
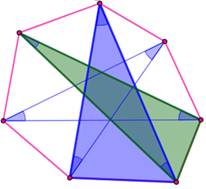
Construction Triangle ABC et carrés extérieurs sur les côtés avec J, K et L pour centres. Le triangle JKL est le triangle de Vecten et son cercle circonscrit est le cercle de Vecten. Le point de concours des droites JB, KA et LC est le point de Vecten extérieur. Propriétés Les droites JB, KA et LC sont les hauteurs du triangle de Vecten. Le point M est son orthocentre. Les deux triangles (ABC et JKL) ont même centre de gravité.
Brèves associées	>>> Kimberling – Nombres de -		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Figure du Moulin à Vent		>>> Mesu

703. Bissection du périmètre du triangle
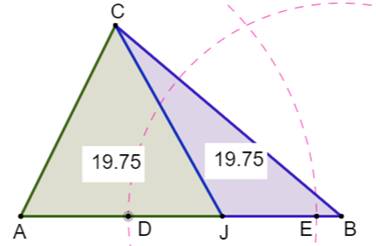
But Partager le périmètre du triangle en deux parties égales. Créer deux triangles de même périmètre à partir du triangle d'origine. Construction Triangle ABC. Cercle (A, BC). Intersection E. Cercle (B, AC). Intersection D. Relier C au milieu de DE. Les triangles CJA et CJB ont le même périmètre.
Brèves associées	>>> Triangle – Périmètre minimum		>>> Brèves Construction – Index
Pour en savoir plus	>>> Bissection du triangle		>>> Triangles – Index

704. Bissection de la surface du triangle
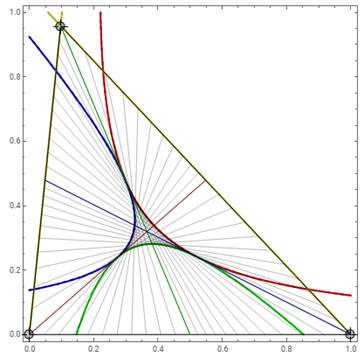
But Partager la surface du triangle en deux parties égales. Créer deux triangles de même aire à partir du triangle d'origine. Commentaire Les trois médianes font l'office. Ce sont les trois seules droites passant par les sommets qui bissectent l'aire du triangle. Sinon, d'une manière générale, il existe une infinité de droites qui partagent le triangle en deux, comme illustrée sur cette figure. Ces droites sont toutes tangentes à trois hyperboles dont les asymptotes sont les droites portant les côtés du triangle. Source image Triangle Area Bisectors – Wolfram – Démonstration interactive
Brèves associées	>>> Triangle – Partage en k parts égales		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Bissection du triangle		>>> Triangles – Index

705. Cardinal et Ordinal
Le cardinal d'une collection d'objets, c'est la quantité totale d'objets dans cette collection, comptés dans n'importe quel ordre. J'ai dix voitures. 10 est un nombre cardinal. L'ordinal est associé à un classement, à une place parmi les autres. Les objets sont mis en ordre. C'est aussi la quantité d'objets avant lui, lui compris. S'il est troisième, c'est qu'il y en a deux avant lui. Je préfère la troisième voiture. 3 est un nombre ordinal.		Cardinal et ordinal en un dessin
Brèves associées	>>> Orthographe des nombres		>>> Brèves Maths – Index
Pour en savoir plus	>>> Cardinaux et ordinaux		>>> DicoMot Math – Lettre C

706. Carré dans le triangle rectangle
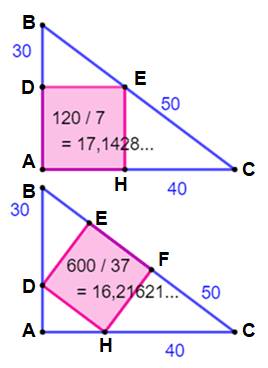
Dimensions du carré inscrit dans un triangle rectangle ? Le long des côtés de l'angle droit Triangles semblables ABC et HEC: Le long de l'hypoténuse Triangles semblables ABC, EBD et FHC:
Brèves associées	>>> Triangle rectangle – Approche	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle rectangle	>>> Carré

707. Triangle rectangle et cercles
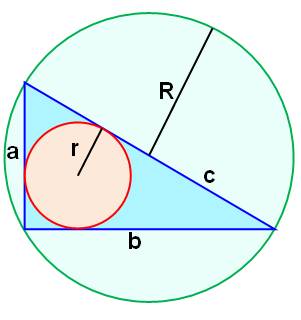
Cercle inscrit et cercle circonscrit du triangle rectangle Les formules exprimant les rayons sont particulièrement simples.
Brèves associées	>>> Cercles dans le carré		>>> Brèves géométrie – Index
Pour en savoir plus	>>> Triangle rectangle et cercles		>>> Sangakus

708. Expression de degré 7
Problème Avec la condition indiquée, démontrer cette identité avec degré 7 au numérateur et degré 4 au dénominateur. Solution (principe) Développer (a + b + c)^k pour k = 2, 3, 4 et 7. Mettre à zéro les termes comprenant le facteur (a + b + c). Un peu d'astuce sera nécessaire !
Brèves associées	>>> Calculs avec radicaux		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Résolution de ce problème		>>> Identiés avec puissances

709. Nombre 56
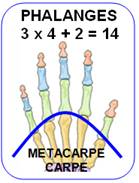
56 = 2^3 x 7 = 8 x 7 = 4 x 14 Notez la succession des quatre chiffres. Un bon moyen pour mémoriser cette multiplication, très souvent récalcitrante ! 56 = 2² + 4² + 6²		56 phalanges pour les quatre membres du corps humain: 2 x 14 pour les mains (illustration), et 2 x 14 pour les pieds.
Brèves associées	>>> Nombre 39		>>> Brèves Nombre – Index
Pour en savoir plus	>>> DicoNombre 56		>>> Mains et pieds

710. Formule de la relativité

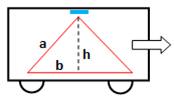
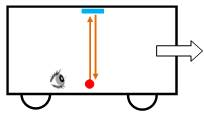
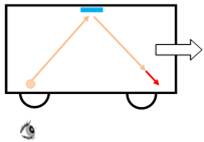
Observateur mobile

Un observateur dans un train.
Un émetteur de lumière au sol. Célérité (vitesse) de la lumière c.

La lumière est réfléchie par un miroir au plafond à une hauteur h.

Pour lui, le temps de parcours de la lumière est:

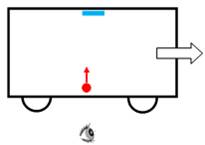
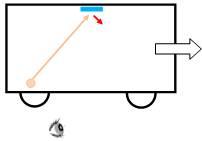
Observateur immobile

Un observateur sur le quai observe le train qui passe à la vitesse V. Trois situations:

1) la lumière est émise

2) la lumière est réfléchie, le train avancé.

3) la lumière est reçue, le train a encore avancé

Pour cet observateur extérieur, la lumière semble parcourir un triangle isocèle. Elle "effectue" le trajet 2a en T' seconde.

Brèves associées

>>> Relativité: Galilée et Einstein

>>> Brèves Sciences – Index

Pour en savoir plus

>>> Analogie de la porte entrebâillée

>>> Relativité de Galilée

>>> Relativité d'Einstein

>>> Einstein – Biographie

>>> Célérité de la lumière

711. Nombre 5040 et ses diviseurs
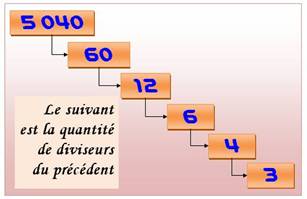
Facteurs du nombre 5 040 Diviseur de 5 040 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45, 48, 56, 60, 63, 70, 72, 80, 84, 90, 105, 112, 120, 126, 140, 144, 168, 180, 210, 240, 252, 280, 315, 336, 360, 420, 504, 560, 630, 720, 840, 1008, 1260, 1680, 2520, 5040. Quantité de diviseurs: 60 Somme des diviseurs: 19 344		La cascade des diviseurs Le nombre 5 040 a 60 diviseurs; lequel 60 a 12 diviseurs; lequel a ….
Brèves associées	>>> Nombre 3 367		>>> Brèves Nombre – Index
Pour en savoir plus	>>> DicoNombre 5 040		>>> Diviseurs

712. Théorème des 15
Image de tous les entiers Le théorème des quatre carrés de Lagrange énonce que tout nombre entier est la somme de quatre carrés: n = x² + y² + z² + t² Un tel polynôme est dit: quadratique (de degré 2), et universel (représente tous les entiers). Outre celui de Lagrange, il existe 54 polynômes quadratiques universels, qui sont capables de représenter tous les nombres entiers positifs.		Théorèmes des 15 Comment reconnaitre ces polynômes qui représentent tous les entiers ? Un théorème qui date du siècle dernier indique qu'il suffit que le polynôme représente les nombres de 1 à 15, et cela suffit pour qu'il représente tous les nombres. Mieux, il suffit qu'il représente seulement neuf de ces nombres:
Brèves associées	>>> Théorie des nombres		>>> Brèves Théorie – Index
Pour en savoir plus	>>> Théorème des 15		>>> Théorème de Lagrange

713. Nombre 211, équilibré
Un nombre premier équilibré est situé à égale distance des deux premiers qui le précède et le suive. Ainsi avec les trois nombres premiers successifs {199, 211, 223}, l'intervalle de chaque côté de 211 vaut 12. Ce nombre 211 est le plus petit premier équilibré avec un écart (E) de 12. Il faut atteindre 16 787 pour avoir le record suivant avec un écart de 24, puis 69 623 pour un écart de 30, etc.
Brèves associées	>>> Nombres 120 et 210		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres premiers équilibrés		>>> Nombre 211

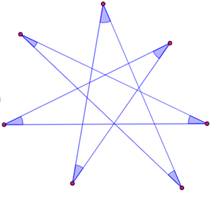
714. Angles de l'heptagone étoilé
Énigme Un heptagone étoilé irrégulier. Quelle est la somme A de tous les angles marqués en bleu? Solution Dessiner le contour de l'heptagone. La somme des angles internes vaut 5. Les sept triangles comme le bleu ou le vert cumulent des angles qui valent 7. Or, tous ces triangles forment bien la totalité des angles internes de l'heptagone avec, toutefois, un doublement des angles bleus (chevauchement triangle bleu et triangle vert). Soit la valeur des angles bleus:		Angles bleus = 180°
Brèves associées	>>> Pentagone de l'arpenteur		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Heptagone étoilé		>>> Heptagone et sa construction

715. Puissances de 2 en 3 et 6
Recherche Recherche des puissances de 2 dont les derniers chiffres sont 3 ou 6. On utilise la propriété suivante: Sachant que 10^n = 2^n × 5^n, on déduit que les nombres de la forme 10^na + b sont divisible par 2^n si et seulement si le nombre b l'est. Alors, on teste la divisibilité des nombres en 3 et 6 de plus en plus grand, divisibles par les puissances de 2 successives.		Les plus petites puissances de 2 en 3 et 6
Brèves associées	>>> Puissances négatives de 2		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Puissances de 2 en 3 et 6		>>> Nombre 6 366 336

716. Aire des bandes dans le triangle
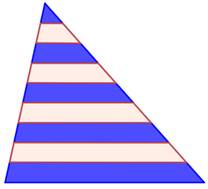
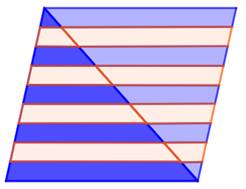
Énigme Un triangle quelconque lardé de bandes, parallèles à un côté et de même largeur. Quelle est le rapport entre les aires des bandes bleues et des bandes roses? Solution La solution est simple ! Elle consiste à faire une copie du triangle et de l'accoler par un des côtés. Alors, les bandes sont prolongées et toutes sont des parallélogrammes de même aire. Il y a cinq bandes bleues et quatre bandes roses. Le rapport est alors: Ce rapport calculé pour le grand parallélogramme est conservé pour le triangle initial qui représente sa moitié. Note Cette astuce ne fonctionne que pour un nombre impair de bandes. La bande du bas doit être accolée à une bande du haut de même couleur.
Brèves associées	>>> Pentagone de l'arpenteur	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle quelconque	>>> Aire

717. Nombres premiers équilibrés
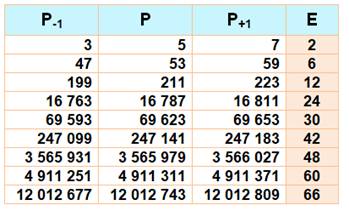
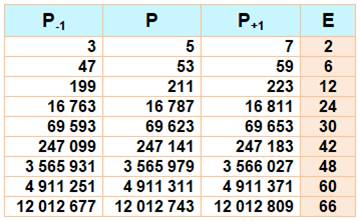
Définition et exemple Un nombre premier équilibré est égal à la moyenne arithmétique de ses deux voisins immédiats. Le nombre premier 53 est voisin des nombres premiers 47 et 59, situés à égale distance de lui-même.		Records, avec E = écart entre premiers
Brèves associées	>>> Conjecture de Goldbach		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombres premiers équilibrés		>>> Moyenne arithmétique

718. Aire du rectangle dans le triangle
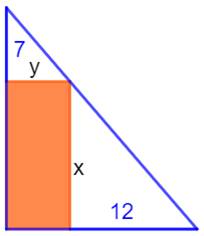
Énigme Un triangle rectangle et un rectangle inscrit. On ne connait que les deux mesures indiquées. Quelle est l'aire du rectangle ? Solution On compare la somme des aires du rectangle et des deux petits triangles et l'aire du triangle complet.
Brèves associées	>>> Aire maximale – problème de Didon	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Rectangle et énigmes diverses	>>> Triangle rectangle

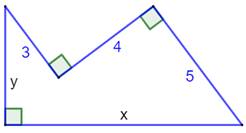
719. Ligne brisée rectangulaire
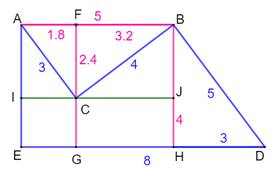
Problème Soit cette ligne brisée fermée comportant trois angles droits. Est-il possible de déterminer les longueurs x et y ? Solution (figure du bas)
Brèves associées	>>> Triangle – Périmètre minimum		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle rectangle – Relations		>>> Triangles semblables

Retour	Brèves de maths – Page 35
Suite	Brèves de maths – Page 37
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve36.htm