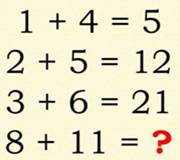NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 40 (780-799)		Page 41 (800-819)		Page 42 (820-839)		Page 43 (840-859)		Page 44 (860-879)
	Page 45 (880-899)		Page 46 (900-919)		Page 47 (920-939)		Page 48 (940-959)		Page 49 (960-979)

BRÈVES de MATHS – Page 49

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

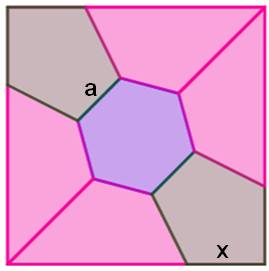
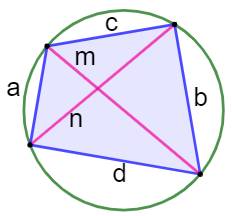
960. Carré partagé en sept
But Découper le carré en sept formes de même aire. On exclut la solution du découpage en sept bandes rectangulaires. L'idée consiste à proposer un hexagone central. Construction Cette construction est impossible à la règle et au compas; il faut calculer et reporter des longueurs. Dans le carré de 7 cm de côté: un hexagone central de 1,64 cm de côté (a) avec une rotation de 45 °. Deux sommets de l'hexagone rejoignent deux sommets du carré (diagonale du carré). Sur les autres sommets du carré, on reporte la longueur x = 2,14, ce qui permet de dessiner les deux pentagones verts. Chacune de ces formes à une aire égale à 7 cm².		Illustration – Voir hexagone Figure construite avec Geogebra avec a = 1,64… et x = 2,14…
Brèves associées	>>> Carré divisé – Aire manquante		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Carré en sept – Calcul de a et x		>>> Carré en

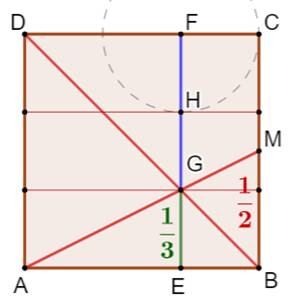
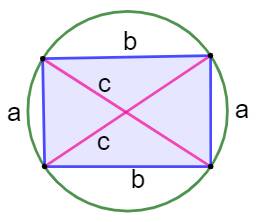
961. Carré partagé en trois bandes
Partage du carré en trois bandes Comment créer trois bandes à la règle et au compas ou même par pliages. Construction Carré ABCD. Diagonale BD. Point M milieu de BC. Segment AM; intersection G. Parallèle en G à BC. Notez que EB = EG (triangle isocèle). Alors GE = 1/3 du côté du carré. Report de la distance GE en FH. Dessin des trois bandes passant par G et H.
Brèves associées	>>> Carré – Trois polygones non-rectangulaires		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Carré en trois bandes rectangulaires		>>> Carré en k bandes

962. Holyèdres
Définition Un holyèdre est objet 3D. C'est un polyèdre dont chacune des faces contient au moins un trou en forme de polygone, et dont les limites des trous ne partagent aucun point entre elles ou avec la limite de la face. Le cube troué n'est pas un holyèdre car les faces crées par les trous doivent aussi être percées. En effet, ce cube troué comporte 4 + 4 × 4 = 20 faces. Solution Ce problème fut posé par Conway en 1997. En 1999, Jade P. Vinson est le premier à présenter un holyèdre avec 78 585 627 faces. En 2003, Don Hatch réussit à trouver un holyèdre à seulement 492 faces.		Contre-exemple Idée du holyèdre 492 en cours de construction
Brèves associées	>>> Compter les hexagones		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Holyèdre		>>> Polyèdres

963. Facteurs les plus probables
Théorème fondamental de l'arithmétique Tout nombre est décomposable en un produit de facteurs unique, à l'ordre des facteurs près.		10 = 2 × 5 (2 et 5 sont les facteurs) 100 = 2² × 5² 121 = 11² 122 = 2 × 61
Facteur les plus probables Parmi tous les nombres, on recense les facteurs les plus fréquents. On n'est pas surpris de trouver le "2" en tête car il est présent dans tous les nombres pairs. Exemple: le nombre 23 est le cinquième nombre le plus fréquent. Les nombres 5 et 7 sont quasiment aussi fréquents l'un que l'autre.		2, 3, 5 et 7, 13, 23, 47, 113, 199, 283, 467, 887, 1627, 2803, 4297, 6397, 10343, 18461, 29453, 43067, 67993, 102679, …
Nombres idéaux Ce sont les nombres formés avec la "factorielle" des nombres les plus probables. Exemple: avec les trois plus petits facteurs, on aura: 2 × 3 × 5 = 30 et avec l'autre possibilité: 2 × 3 × 7 = 42.		6, 30, 42, 390, 546, 8970, 12558, 421590, 590226, 47639670, 66695538, 9480294330, 13272412062, …
Brèves associées	>>> Nombres intouchables	>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres idéaux	>>> Factorielle >>> Théorème fondamental de l'arithmétique

964. Nombre et couples de premiers
Conjecture de Golbach Tout nombre pair > 3 est la somme de deux nombres premiers. Conjecture vérifiées jusqu'à des nombres astronomiques, mais pas prouvée. Formulation 2n = p + q n + n = p + q Exemple 14 = 3 + 11 7 + 7 = 3 + 11 Le nombre 14 est la somme des deux nombres premiers 3 et 11. Le nombre est la moyenne arithmétique de 3 et 11 (la demi somme).		Conjecture du couple équidistant Tout nombre n > 3 est à égale distance d'un couple de nombres premiers, au moins une fois. Every integer n > 3 is halfway between two primes. Cet énoncé surprenant est, en fait, une autre manière d'exprimer la conjecture de Goldbach. Formulation n + n = p + q n – p = q – n Exemple 7 + 7 = 3 + 11 7 – 3 = 11 – 7 4 = 4 Le nombre 7 est à égale distance des nombres premiers 3 et 11.
Brèves associées	>>> Carré = Somme de cubes		>>> Brèves Identités – Index
Pour en savoir plus	>>> Mi-distance		>>> Conjecture de Golbach

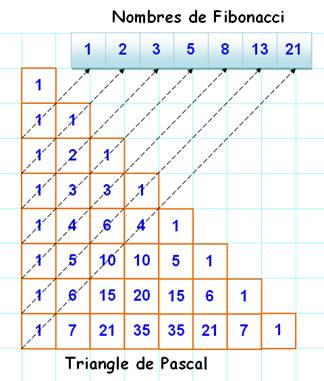
965. Fibonacci & Pascal
Suite de Fibonacci Suite de nombres commençant par (0, 1) et telle que chaque terme suivant est la somme des deux précédents. 0,1, 1, 2, 3, 5, 8, 13, 21, … Triangle Pascal Triangle de nombres tel que chaque terme est la somme des deux du "haut". Ainsi, en dernière ligne, 21 = 6 + 15. Chaque ligne du triangle de Pascal indique les coefficients du binôme à une certaine puissance: (a + b)^3 = 1a^3 + 3a^2b + 3ab^2 + 1b^3 Propriété Dans le triangle de Pascal, la somme des "diagonales" forment la suite de Fibonacci.		Relation Fibonacci – Pascal
Brèves associées	>>> Pascal – Nombres 1, 3, 3, 1		>>> Brèves Suites – Index
Pour en savoir plus	>>> Fibonacci et Pascal		>>> Coefficients du binôme

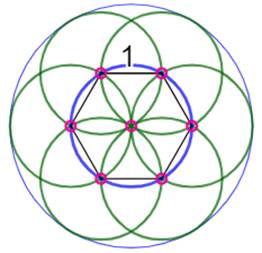
966. Cercle minimal de points distants
Théorème Un ensemble de sept points mutuellement distance de une unité au moins est contenu dans un disque (y compris la frontière) de rayon unité au moins (diamètre 2). Soit: D(7) = 2. Les sept points sont les sommets d'un hexagone régulier accompagné du centre. Notez que le disque inclut sa circonférence. Bateman et Erdös ont prouvé ce théorème.		Cas de sept points – Solution limite
Brèves associées	>>> Cercle de Conway		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercle minimal de points distants		>>> Cercle – Index

967. Nombres k-Harshad
Nombres de Harshad Ce sont les nombres divisibles par la somme de leurs chiffres. Ex 882 / (8 + 8 + 2) = 49 Le nombre 49 est un 49-Harshad. Il existe seulement trois tels nombres: 441, 735, 882 La plus grande quantité avec 37 [111, 222, 333, 370, 407, 444, 481, 518, 555, 592, 629, 666, 777, 888, 999] Ces quinze nombres sont tous 37-Harshad. Il n'en existe pas plus.		Les multi k-Harshad jusqu'à k = 25 H1, 9, [1, 2, 3, 4, 5, 6, 7, 8, 9] H4, 4, [12, 24, 36, 48] H7, 4, [21, 42, 63, 84] H10, 10, [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] H13, 2, [117, 156, 195] H16, 2, [144, 192, 288] H19, 11, [114, 133, 152, 171, 190, 209, 228, 247, 266, 285, 399] H22, 3, [132, 264, 396] H25, 3, [150, 225, 375]
Brèves associées	>>> Super-Harshad		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres k-Harshad		>>> Chiffres – Index

968. Nombres McNugget
Le problème Le restaurant ne sert que des barquettes de Nuggets de 4, 6 ou 20 pièces. Est-il possible d'acheter n'importe combien de pièces ? Non, mais à partir d'une certaine quantité, c'est toujours possible. Quelle est la valeur limite ? Les quantités impossibles ne sont pas des nombres McNugget. La limite est appelé nombre de Frobenius.			Barquettes 6, 9 et 20 Nombres NON-McNugget: 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, 43. Nombre de Frobenius: 43. En ajoutant une barquette de quatre nuggets, toutes les combinaisons sont possibles sauf 1, 2, 3, 5, 7 et 11.
Brèves associées	>>> Le faux billet de 50 euros	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Nombres McNugget (Frobenius)	>>> Chameau et bananes

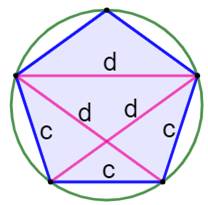
969. Beauté du Th. de Ptolémée
Théorème de Ptolémée		Théorème de Pythagore		Nombre d'or d² – d – 1 = 0 est l'équation du nombre d'or
Brèves associées	>>> Approche du théorème		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Ptolémée		>>> Théorème de Pythagore >>> Pentagone et nombre d'or

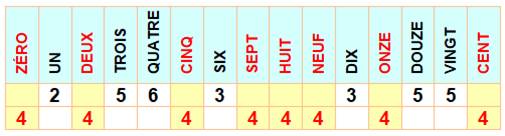
970. Nombres et lettres
Nombres écrits avec exactement quatre lettres Quizz: quel nombre prolonge la suite: 0, 2, 5, 7, 8, 9, 11, ? Réponse: 100. Quizz: quelle lettre prolonge cette suite: Z, U, D, T, Q, ? Réponse: C. Quizz: quel nombre prolonge cette suite: 1, 6, 0, 3, 4, 14, 26 ? Réponse: 22.			Quantité de lettres record 2 – UN 3 – SIX 4 – ZÉRO 5 – TROIS 6 – QUATRE 8 – QUATORZE 9 – VINGT-SIX 10 – VINGT-DEUX
Brèves associées	>>> Liste des quantité de lettres	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Nombres et lettres	>>> Nombre 4

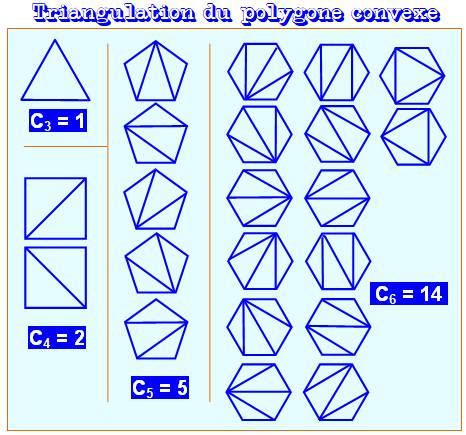
971. Nombres de Catalan
Bref historique Alors qu'ils étaient connus des Chinois (1730), c'est Euler (1760) qui les redécouvre en comptant les triangles réalisés en traçant les diagonales non concourantes d'un polygone convexe. Depuis, pratiquement tous les mathématiciens se sont intéressés aux nombres qui deviendront ceux de Catalan en 1948 après avoir été les nombres de Segner. Eugène Catalan (1838) étudie les combinaisons de lettres et de parenthèses et les associe aux nombres de Segner-Euler. Aujourd'hui, on connait plusieurs centaines de cas d'applications des nombres de Catalan. Richard Stanley en publie 214 en 2015. La page consacrée aux nombres de Catalan est sans doute la plus importante de l'Encyclopédie des suites d'entiers (OEIS A000108).
Brèves associées	>>> Nombres de Dudeney		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres de Catalan >>> Triangulation des polygones		>>> Suites pour compter

972. Énigme trompeuse

Énigme fallacieuse (trompeuse)

Solution

1	+	4	+	0	=	5
2	+	5	+	5	=	12
3	+	6	+	12	=	21
4	+	7	+	21	=	32
5	+	8	+	32	=	45
6	+	9	+	45	=	60
7	+	10	+	60	=	77
8	+	11	+	77	=	96

Énigme correctement posée

Commentaire

Énigme courante sur le Web. Il faut savoir que ces égalités sont fausses et le problème est de les rétablir en posant correctement les opérations sans tenir compte des signes opératoires.

Trois astuces principales: le report comme ici ou une combinaison linéaire des nombres ou une opération avec les chiffres.

Brèves associées

>>> Autre énigme virale

>>> Brèves Énigmes – Index

Pour en savoir plus

>>> Énigmes virales sur le Web

>>> Énigmes et jeux

973. Arabesques
Arabesques Formes géométriques répétitives souvent utilisées pour orner les monuments arabes (islamiques). Souvent composés d'entrelacs de feuilles, de fleurs et de vignes. D'autres sont réalisés à partir d'un motif géométrique répétitif, utilisé comme pavage du plan. Ces motifs sont connus sous le nom d'arabesque en Occident; ils sont appelés zakhrafa en Orient (culture islamique), et islimi en Turquie. Arabesque octogonale L'illustration montre un exemple d'arabesque géométrique construite à partir d'un octogone régulier.
Brèves associées	>>> Sangaku		>>> Brèves Construction – Index
Pour en savoir plus	>>> Arabesques – Construction		>>> Pavage >>> Octogone régulier

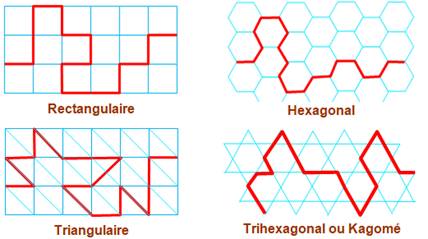
974. Réseaux ou grille
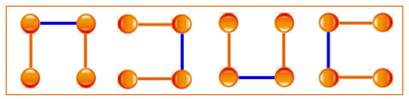
Parcourir la grille On se donne un quadrillage régulier dit grille ou réseau (anglais: grid or lattice). On dessine une ligne brisée qui relie certains points du quadrillage: c'est un chemin de grille (anglais (lattice path). Il peut être orienté ou non. Chemin ou trajectoire Selon les contraintes de parcours, il existe plus ou moins de chemins pour relier deux points en suivant les traits de la grille. La question que l'on se pose: comment calculer la quantité des chemins possibles ?		Quelques exemples de réseaux et chemins
Brèves associées	>>> Sangaku		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Réseaux		>>> Graphe – Index

975. Graphes isomorphiques
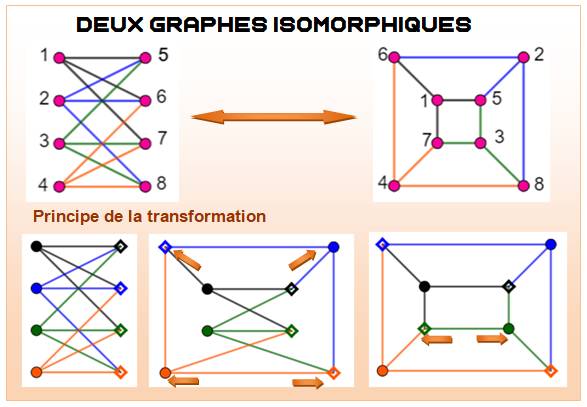
Isomorphisme entre graphes Graphes qui se ressemblent par rotation ou symétrie (exemple en haut) ou même par déplacement des sommets tout en conservant les connexions (exemple du bas).		Exemple de quatre graphes isomorphiques
Brèves associées	>>> Ponts de Königsberg		>>> Brèves Graphes – Index
Pour en savoir plus	>>> Graphes simples à cinq sommets		>>> Morphisme

976. Quarante mille en quatre chiffres
Jeu des quatre chiffres Avec chacun des neuf chiffres utilisés quatre fois, reconstituer le nombre 40 000 et cela, en utilisant les opérations arithmétiques. Note sur la fonction gamma: Γ(n) = (n-1)! C'est un moyen d'avoir accès à la factorielle d'autres nombres. Ex: Γ(3!) = Γ(6) = 5! = 120. On utilise le point décimal: .4 au lieu de 0,4; s'il est surligné, il vaut 0,444… = 4/9. Chaque expression trouvée (colonne de gauche) est explicitée en colonne de droite. Le cas des quatre "4" est un problème classique et populaire.		D'après Four fours – Nidi Guru
Brèves associées	>>> Somme paradoxale de Ramanujan		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Nombre 40 000 en quatre chiffres >>> Jeu des quatre "4" (four fours) >>> Autres jeux de ce type		>>> Fonction gamma >>> Point décimal

977. Graphe – Devinette
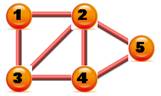
Exemple de graphe à cinq sommets et sept arêtes Degré des sommets C'est la quantité d'arêtes aboutissant à ce sommet. Règle des sommets-arêtes La quantité d'arêtes est égale à la moitié de la somme des degrés. Suite des degrés des sommets du graphe ci-dessus S = (2, 4, 3, 3, 2) Somme: 14 Le graphe compte: 14 / 2 = 7 arêtes		Devinette: application de la règle des sommets-arêtes Une assemblée de neuf personnes. On se sert la main en signe de bienvenue. Est-il possible que chaque personne salue sept personnes exactement ? Ce problème revient à considérer un graphe à neuf sommets dont chacun aurait un degré égal à 7. Le somme des degrés serait 9 × 7 = 63, un nombre impair, donc non divisible par 2. Ce cas est impossible selon la règle des sommets-arêtes. Réalisable si au moins un (en fait un nombre impair) de personnes avait serré la main d'un nombre pair de personnes dans l'assemblée. Cette fois, ils sont dix. Ils se saluent tous. Combien de poignées de mains ? Ce problème revient à considérer un graphe à dix sommets dont chacun relie les neuf autres. La somme des degrés vaut: 10 × 9 = 90. Le graphe possède 45 arêtes. Il y a eu 45 poignées de mains.
Brèves associées	>>> Nœuds, entrelacs et tresses		>>> Brèves Graphe – Index
Pour en savoir plus	>>> Graphes - Introduction		>>> Graphes – Index

978. Compter les triangles
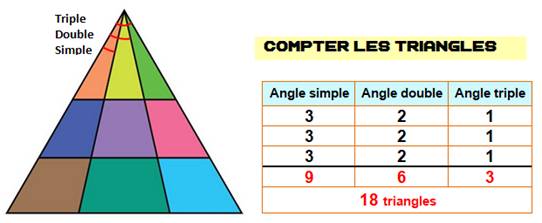
Cette énigme passe pour être difficile ou, en tout cas, considérée comme source de pièges. La réponse souvent donnée est 9. Mais c'est le double. En fait, un peu de méthode (tableau) est le compte est bon !
Brèves associées	>>> Triangle en carrés – Calcul de l'aire		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Compter les triangles >>> Énigmes virales sur le Net		>>> Jeux et énigmes – Index

979. Somme des angles
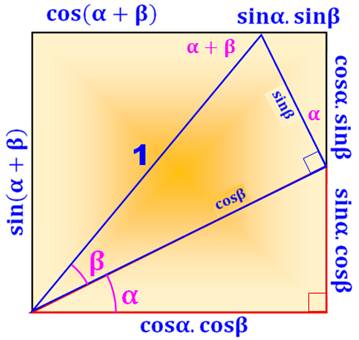
Résumé en image Les angles alpha et bêta sont visualisés en rose. On a dessiné le triangle rectangle avec un angle alpha; alors que celui avec l'angle bêta lui est adjacent par l'hypoténuse. Les longueurs se lisent immédiatement sur la figure. Notez bien le segment unitaire (hypoténuse du triangle rectangle d'angle bêta).
Brèves associées	>>> Somme de carrés de sinus		>>> Brèves Trigonométrie – Index
Pour en savoir plus	>>> Somme des angles – Démonstration		>>> Identités trigonométriques – Index

Retour	Brèves de maths – Page 48
Suite	Brèves de maths – Page 50
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve49.htm