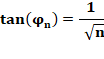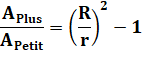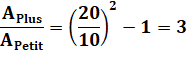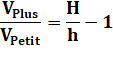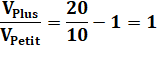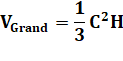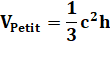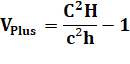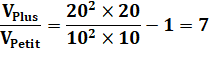NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 24

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

(Note au rédacteur: 460, 461 et 462 ont été référencées en 480, 481, 481 par erreur)

460. Angle inconnu
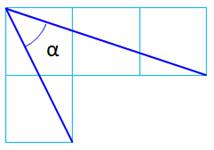
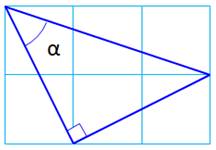
Énigme Dans ce quadrillage carré, quelle est la valeur de cet angle? Solution Fermer le tracé bleu. Le segment dessiné est de même longueur que celui de gauche. L'angle en bas est un angle droit. Le triangle formé est isocèle rectangle et l'angle vaut 45°.
Brèves associées	>>> Parallélogramme divisé – Calcul de l'aire		>>> Trois souris sur triangle
Pour en savoir plus	>>> Triangle isocèle rectangle		>>> Angles

461. Théorème du pitre à bord
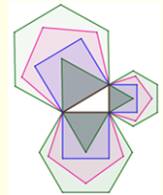
Théorème de Pythagore Il dit que a² + b² = c². On traduit par: l'aire du grand carré est égale à la somme des aires des deux petits carrés, chacun des carrés étant apposé sur les côtés d'un triangle rectangle. Théorème du pitre à bord Si on remplace les carrés par un voilier avec un clown dessus, l'aire du grand voilier avec son personnage est égale à la somme des aires des deux figures semblables posées sur les côtés du triangle rectangle. Valable pour toute figure même biscornue pourvu que les trois soient semblables (proportionnelles aux longueurs des côtés).		Généralisation du théorème de Pythagore L'aire de la figure sur l'hypoténuse est égale à somme des aires des deux figures semblables construites sur les deux côtés du triangle rectangle.
Brèves associées	>>> Théorème de Pythagore - Visuel		>>> Triplets de Pythagore – Proportions
Pour en savoir plus	>>> Théorème de Pythagore >>> Ses généralisations		>>> Triangle rectangle >>> Triangles semblables

462. Périmètre du triangle inscrit
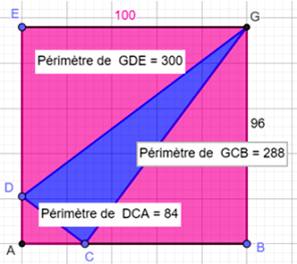
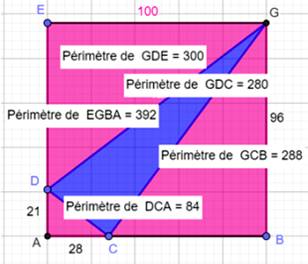
Énigme Un rectangle ABGE (100 x 96). Ayant choisi les points D et C, on trouve les périmètres des trois triangles rectangles périphériques: 300, 288 et 84. Quel est le périmètre du triangle bleu ? Solution Périmètre du rectangle: PR = 2 x (100 + 96) = 392 La somme des périmètres des trois triangles roses vaut: P3 = 300 + 288 + 84 = 672. Elle représente une fois le périmètre du rectangle auquel on ajoute le périmètre du triangle bleu PTB . P3 = PR + PTB PTB = P3 – PR = 672 – 392 = 280 Remarque Le quadrillage montre que les valeurs ne sont pas choisies au hasard. Les longueurs des côtés du triangle bleu sont des nombres entiers. Ce qui implique que les triangles roses sont des triangles de Pythagore: 100² + 75² = 125² 96² + 28² = 100² 28² + 21² = 35²
Brèves associées	>>> Carré divisé – Aire manquante		>>> Rectangle divisé en neuf – Son périmètre
Pour en savoir plus	>>> Triangle dans le carré		>>> Carré – Index

463. Partager le triangle en k parts égales
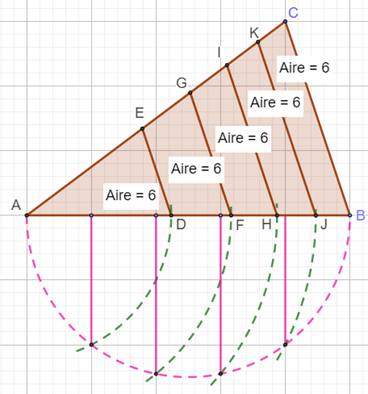
Comment partager un triangle en k tranches de même aire, avec des droites parallèles à un des côtés ? Construction pour k = 5 Diviser AB en cinq segments égaux. Tracer les perpendiculaires (roses) à AB à partir des quatre points. Elles interceptent le demi-cercle AB en quatre points. Tracer les arcs de cercle (verts) à partir de A et qui passent par ces quatre points. Ils coupent AB en quatre points (D, F, H, J). À partir de ces quatre points, tracer les parallèles au côté BC. Elles partagent le triangle ABC en cinq polygones (un triangle et quatre trapèzes) de même aire.
Brèves associées	>>> Triangle et les nombres 3, 4, 5, 6		>>> Demi-cercle dans le triangle isocèle
Pour en savoir plus	>>> Triangle et médianes		>>> Partage du triangle en parts égales

464. Nombres intouchables
Diviseurs stricts de 12 : 1, 2, 3, 4, 6 Leur somme, parfois nommée somme aliquote, est égale à 16. On dit que le nombre 16 est atteint (touché) par cette somme de diviseurs. Le nombre 16 est un nombre touchable dont l'antécédent est 12. Si on calcule la somme pour tous les nombres, existe-il des nombres qui ne sont jamais somme de diviseurs ? Oui ! Ce sont les intouchables.		Nombres intouchables jusqu'à 150 2, 5, 52, 88, 96, 120, 124, 146. Nombres touchables, combien de fois ? Le nombre 31 est touchable cinq fois avec la somme des diviseurs stricts de 32, 125, 161, 209 et 221. C'est le plus petit avec cinq antécédents: il est hautement touchable. Le suivant est 49 avec six antécédents: 75, 215, 287, 407, 527, 551.
Brèves associées	>>> Nombres narcissiques		>>> Diviseurs
Pour en savoir plus	>>> Nombres intouchables		>>> Suite aliquote

465. Spirale de Théodore de Cyrène
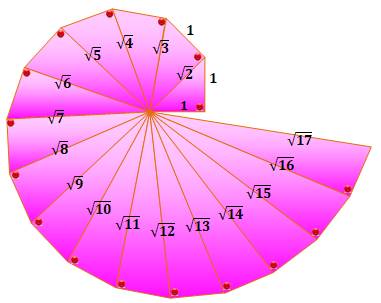
Cette spirale est aussi appelée: escargot de Pythagore ou spirale d'Einstein. Sa construction très simple permet de construire la racine carrée des nombres successifs. Construction Un triangle rectangle isocèle ce côté1. On y accole un triangle rectangle avec pour hypoténuse le côté du triangle précédent et un côté extérieur de longueur 1. Valeur de l'angle du triangle n
Brèves associées	>>> Lemniscate		>>> Angles dans trois carrés
Pour en savoir plus	>>> Spirale de Théodore de Cyrène		>>> Spirales

466. Carré magique 6x6
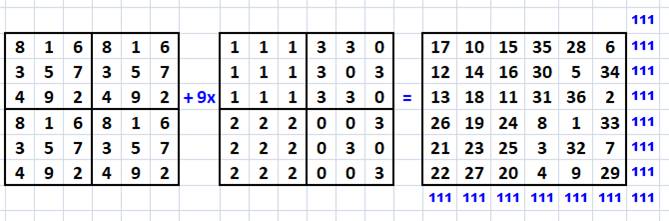
Il existe de nombreuses méthodes pour construire les carrés magiques dont cette méthode par copie d'un carré magique connu d'ordre moitié. Cette méthode est générale pour passer d'un carré magique d'ordre n à un carré magique d'ordre 2n.		La méthode par copie d'un carré moitié consiste à partir d'un carré magique 3x3, reproduit quatre fois, pour réaliser un carré 6x6. Un autre carré est formé de (0, 1, 2 et 3). Le carré magique est calculé en sommant le premier carré avec neuf fois le deuxième. Le calcul est effectué pour chaque cellule avec les cellules de même rang.
"CM 3x3" + 9 (tableau de permutations) = "CM 6x6" Exemples de calcul: 8 + 9 x 0 = 8; 8 + 9 x 2 = 26; 1 + 9 x 0 = 1; 1 + 9 x 2 = 19; etc.
Brèves associées	>>> Carré magique 5x5		>>> Grilles et carrés magiques – Index
Pour en savoir plus	>>> Carré magique 6x6		>>> Carrés magiques – Index

467. Nombre 2 520
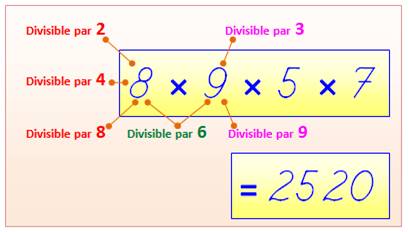
Plus petit nombre divisible par tous les nombres de 1 à 9 2 520 = 3 × 4 × 5 × 6 × 7 = 5 × 7 × 8 × 9 = 8! / 4² = 8! / (2 × 2!)² = 8! / 2^4 = 9! / 12² = 9! / (2 × 3!)² = (2+2+2+2)! / (2!×2!×2!×2!) Ne pas confondre avec les factorielles 9 ! = 1 × 2 ×3 × 4 × 5 × 6 × 7× 8 × 9 = 362 880 = 2 520 × 12^2 = 2 5 20 × 2^4 × 3^2
Brèves associées	>>> Nombre 2 019			>>> Nombres en brèves – Index
Pour en savoir plus	>>> Nombre 2 520	>>> PPCM			>>> Factorielles

468. Aire de la couronne
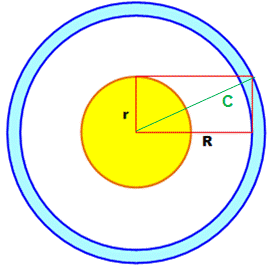
Aire disque jaune: Aire couronne bleue: Aire bleue = Aire jaune
Brèves associées	>>> Périmètre et aire		>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Aire de la couronne et autres		>>> Cercle – index

469. Puissances négatives de 2
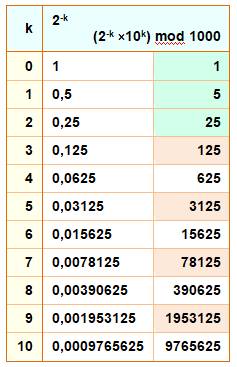
Les puissances négatives de 2 se terminent alternativement par 125 et 625, sauf les trois premières.
Brèves associées	>>> Puissances et divisibilité par 5		>>> Opérations en brèves – Index
Pour en savoir plus	>>> Puissances négatives de 2		>>> Puissances négatives

470. Triangle rectangle de Conway
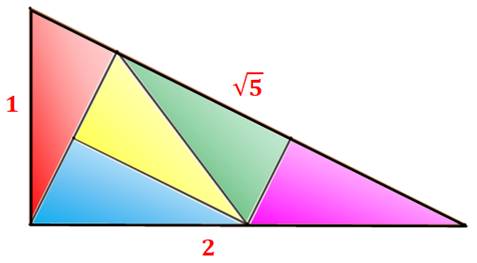
Définition Le triangle rectangle de côtés 1 et 2, son hypoténuse est donc racine de 5, peut être découpé en cinq triangles identiques et, chacun, semblable au grand.
Brèves associées	>>> Triangle – Partage en six parts égales		>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Triangle de Conway		>>> Triangle rectangle

471. PIZZA en plus
Énigme Mon petit frère a eu une pizza de 10 cm de rayon et moi 20 cm. J'ai combien de pizza en plus en proportion de la petite ?		Aire du disque		Avec les nombres
Conclusion		J'ai en plus, trois fois l'équivalent de la pizza de mon frère.
Petit malin, sans calcul …		Ma pizza est deux(2) fois plus grosse en taille, donc quatre (2²) fois plus grosse en surface. J'ai donc, en plus, trois fois la pizza de mon frère.
Brèves associées	>>> Pizza – Choix de la taille		>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Aire du disque		>>> Aires >>> Aires des formes classiques

472. JUS d'ORANGES en plus
Énigme Mon petit frère a eu 10 cm de jus d'orange dans le pichet et moi 20 cm. J'ai combien de jus en plus en proportion de la dose de mon frère ?		Volume du cylindre		Avec les nombres
Conclusion		J'ai en plus, une fois l'équivalent du jus d'orange de mon frère.
Petit malin, sans calcul …		Ma pichet est deux(2) fois plus haut que celui de mon frère, donc deux fois plus de jus que lui. J'ai donc, en plus, une fois de plus la dose de mon frère.
Brèves associées	>>> Volume de la pizza – Humour		>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Volume du cylindre		>>> Volume – Formulaire >>> Volume des formes particulières

473. PYRAMIDE en plus
Énigme Mon petit frère construit une pyramide à base carrée de 10 cm et haute de 10 cm. Moi, une de 20 cm de côté et 20 cm de haut. Mon frère finit sa pyramide en une heure. Je mettrai combien de temps en plus pour construire ma pyramide ?			Volume de la pyramide		Avec les nombres
Conclusion		Si mon frère met une heure pour construire sa pyramide, il me restera encore 7 heures de travail pour finir la mienne.
Petit malin, sans calcul …		Le volume est deux fois plus grand dans les trois dimensions. Il est donc huit (2^3) fois plus volumineux. Je mettrai donc, en plus, sept fois le temps mis par mon frère.
Brèves associées	>>> Volume de la pizza – Humour			>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Pyramide			>>> Volume – Formulaire >>> Volume des formes particulières

474. Carrés et pannumériques
Quatre carrés couvant tous les chiffres		Ces quatre nombres couvrent tous les chiffres avec leur carré, et leur somme est minimale: 3², 9², 18², 24² => 9, 81, 324, 576 (somme 54) Les quatre nombres couvrant aussi le 0: 3², 9², 24², 48² => 9, 81, 576, 2304 (somme 84) Le plus petit nombre au carré avec tous les chiffres 139 854 276 = 11 826² Le plus grand nombre au carré avec tous les chiffres 923 187 456 = 30 384²
Brèves associées	>>> Repunits et palindromes pannumériques			>>> Motifs en brèves – Index
Pour en savoir plus	>>> Pannumériques et carrés		>>> Pannumériques carrés

475. Horloge romaine – Énigme
La somme des nombres sur une horloge, romaine ou non, est égale à 78. On vous propose néanmoins de la partager en quatre parties chacune contenant des nombres dont la somme est 20. Notez qu'il s'agit d'une horloge où le quatre est noté avec quatre barres au lieu de IV. Ce qui est courant sur les horloges pour conserver un effet de symétrie avec le huit.
Brèves associées	>>> Horloge avec formules mathématiques		>>> Jeux en brèves – Index
Pour en savoir plus	>>> Jeux avec les chiffres romains		>>> Horloges et maths

476. Carrés et le nombre 5
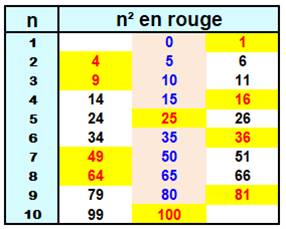
Un nombre au carré est un multiple de 5 ou un voisin. Si vous calculez mentalement un carré, vérifiez qu'il est un multiple de 5 ou alors qu'il s'en écarte d'une seule unité. Exemple: 123 456 789² = 15 241 578 750 190 521		Le chiffre des unités d'un carré est: {0, 1, 4, 5, 6, 9}, jamais 2, 3, 7 ou 8.
Brèves associées	>>> Cubes et divisibilité par 6		>>> Opération en brèves – Index
Pour en savoir plus	>>> Formes des carrés		>>> Carrés

477. Somme de cubes
Énigme La somme de deux nombres est 13. La somme des cubes est 637. Quels sont ces deux nombres. Méthode Écrire les égalités avec soin. Un tableau fait parfaitement l'affaire. Ici, on a recours à une identité remarquable du troisième degré. On y retrouve opportunément la somme et la somme des cubes.		Solution
Brèves associées	>>> Équations diophantiennes		>>> Équations en brèves – Index
Pour en savoir plus	>>> Identités remarquables (3^e degré)		>>> Jeux et énigmes

478. Trouver le nombre premier
Énigme Trouver le nombre premier entre 524 282 et 524 290. Solution Énumérons ces nombres en éliminant les nombres pairs et les nombres divisibles par 5: 524 283, 524 287, 524 289. Test de divisibilité par 3: 5+2+4 = 11 => 2+2+8 => 12 => 3+3 = 6 => divisible par 3. 5+2+4 = 11 => 2+2+8 => 12 => 3+7 = 10 => non divisible par 3. 5+2+4 = 11 => 2+2+8 => 12 => 3+9 = 3 => divisible par 3. Sachant qu'il existe un nombre premier, c'est 524 287.		Commentaire La plage commence à 524 282, car avec 524 280 ce serait plus dur ! En effet: 524 281 = 269 x 1949, deux grands facteurs difficiles à identifier. Facteurs des nombres de cette plage 524280 = 2^3 × 3 × 5 × 17 × 257 524281 = 269 × 1949 524282 = 2 × 11 × 23 831 524283 = 3 × 174 761 524284 = 2^2 × 131 071 524285 = 5 × 23 × 47 × 97 524286 = 2 × 3^3 × 7 × 19 × 73 524287 = 524 287 Premier 524288 = 2^19 Puissance de 2 524289 = 3 × 174 763 524290 = 2 × 5 × 13 × 37 × 109
Brèves associées	>>> Premiers en 6k+1 et 6k+5		>>> Brèves sur les premiers – Index
Pour en savoir plus	>>> Nombre 524 287 >>> Nombres premiers >>> Facteurs		>>> Divisibilité par 3 >>> Puissances de 2

479. Dizaines sans nombre premier

Les plages en dizaines comportent de 0 à 4 nombres premiers.

La plage 200 à 209 est la plus petite sans nombres premiers.

Aucun premier de 200 à 209

200 = 2³ × 5²

201 = 3 × 67

202 = 2 × 101

203 = 7 × 29

204 = 2² × 3 × 17

205 = 5 × 41

206 = 2 × 103

207 = 3² × 23

208 = 2⁴ × 13

209 = 11 × 19

Dizaines sans nombre premier

200, 320, 510, 530, 620, 840, 890, 1070, 1130, 1140, 1260, 1330 …

Il y a quatre premiers de 10 à 19 (11, 13, 17 et 19)

10	4	50	2	350	2	240	1
100	4	60	2	370	2	290	1
190	4	80	2	380	2	300	1
0	3	150	2	400	2	360	1
40	3	160	2	440	2	390	1
70	3	170	2	490	2	410	1
130	3	230	2	500	2	420	1
220	3	250	2	90	1	450	1
310	3	260	2	110	1	470	1
430	3	270	2	120	1	480	1
460	3	280	2	140	1	200	0
20	2	330	2	180	1	320	0
30	2	340	2	210	1

Brèves associées

>>> Premiers au carré = 24k + 1

>>> Brèves sur les premiers – Index

Pour en savoir plus

>>> Nombre 200

>>> Nombres premiers

Retour	Brèves de maths – Page 23
Suite	Brèves de maths – Page 25
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve24.htm