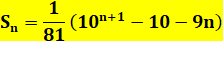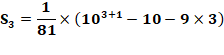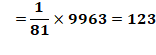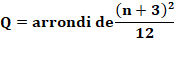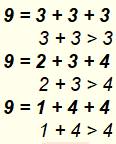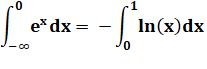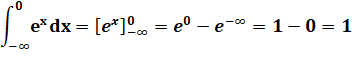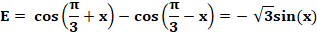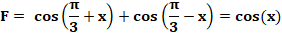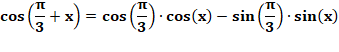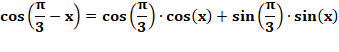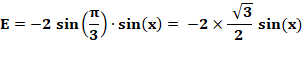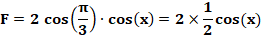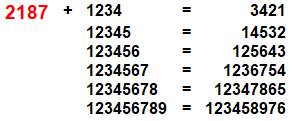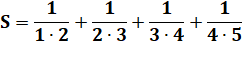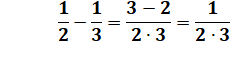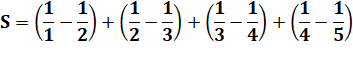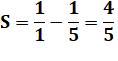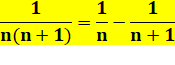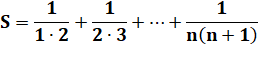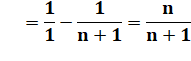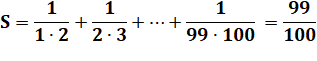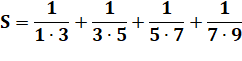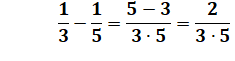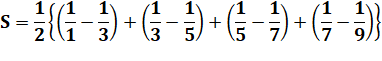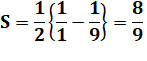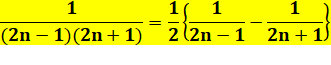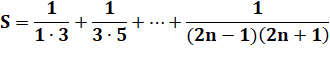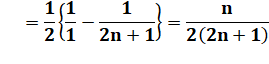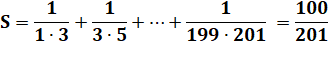|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 39 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
760. Nombres à anagrammes premières |
|
|||
|
Formation des
nombres À partir d'un nombre, on élabore
toutes les combinaisons possibles avec ses chiffres. Parmi ces nouveaux nombres, on
sélectionne les nombres premiers. Nombres
multi-premiers par combinaisons Le nombre 13 offre quatre combinaisons (1, 3, 13, 31) dont
trois sont premières. Le nombre 34 en produit quatre sur quatre. Le nombre 113 prend le record suivant avec sept
premiers sur huit combinaisons. Le nombre 137 le
bat avec 11 sur 15. |
Records 13, 3 / 4, {3, 13, 31}
37, 4 / 4, {3, 7, 37, 73}
113, 7 / 8, {3, 11, 13, 31, 113, 131, 311} 137, 11 / 15, {3, 7, 13, 17,
31, 37, 71, 73, 137, 173, 317}
1123, 18 / 34, {2, 3, 11, 13, 23, 31, 113, 131, 211, 311, 1123, 1213, 1231, 1321, 2113,
2131, 2311, 3121} 1139, 20 / 34, {3, 11, 13, 19,
31, 113, 131, 139, 191, 193, 311, 911, 1193, 1319, 1913, 1931, 3119, 3191,
3911, 9311} |
|||
|
Brèves associées |
>>>
Anagramme
des nombres |
>>>
Brèves Type de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres multi-premiers |
>>>
Compter les anagrammes des nombres |
||
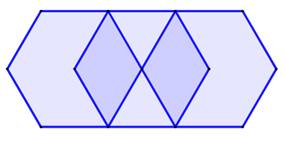
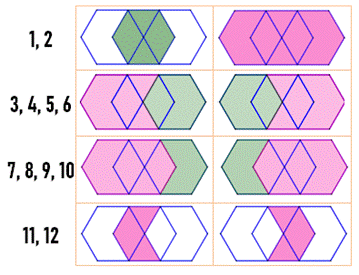
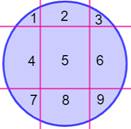
761. Compter les hexagones |
|
|||
|
Énigme Sur cette
figure, trois hexagones réguliers enchevêtrés. Combien
d'hexagones comptez-vous: trois ou plus ? Oui, il faut compter tous les
hexagones réguliers, ou non. Solution La figure
contient douze hexagones. Ils sont
présentés ci-contre. |
|
|||
|
Brèves associées |
>>>
Hexagone
et triangles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Pentagone
|
>>>
Polygone – Index |
||
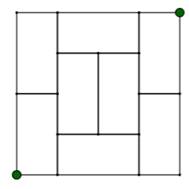
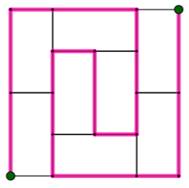
762. Chemin sur une grille |
|
|||
|
Énigme Sur cette grille, quel est le parcours le plus long pour rejoindre les
deux points verts ? Solution Deux
sortes de spirales issues de chacun des points. Le chemin
fait alors 22 unités. |
|
|||
|
Brèves associées |
>>>
Château et douves |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Labyrinthes |
>>> Jeux de grilles
et autres |
||
763. Pyramide de nombres |
|
|||
|
Nombre pannumérique Un nombre pannumérique est un nombre formé avec tous les chiffres
comme 123456789 ou autres dans le désordre, avec le 0 ou non. Ils sont source d'une grande
variété d'amusements. La somme de ces chiffres étant 1 + 2 + … 9 = 9 x 10/2 = 45, les
nombres pannumériques sont tous divisibles par 9. Un des jeux classiques consiste à atteindre un nombre donné en
utilisant tous les chiffres dans un jeu d'opérations classiques. Exemples 100 = 123 – 45 – 67 + 89 666 = 1 + 2 + 3 + 4 + 567 + 89 |
|
|||
|
Brèves associées |
>>>
Puissances des chiffres |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Pépites de nombres |
>>>
Nombres pannumériques |
||
764. Somme des repunits |
|
|||
|
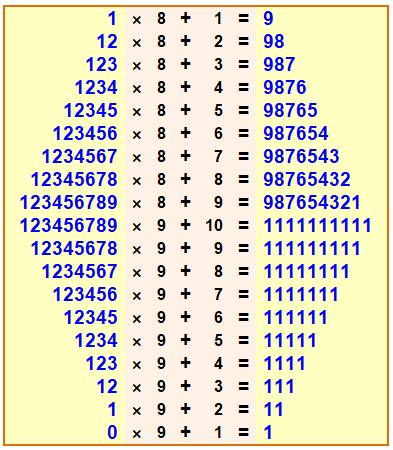
Observation La somme des
repunits successifs (un chiffre, deux chiffres, …) produit un motif répétitif
formé principalement de la succession des chiffres. 1 + 11 +
111 + 1111 = 1234 Formule de calcul
Exemple
|
|
|||
|
Brèves associées |
>>>
Somme de
fractions |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Somme des repdigits |
>>>
Redigits |
||
765. Partitions à trois termes |
|
|||
|
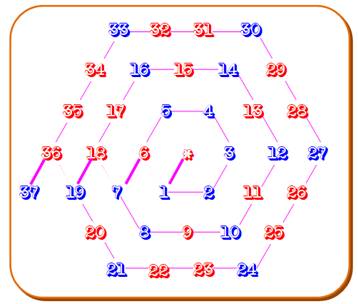
Il existe sept partitions du nombre dont cinq
comportent jusqu'à trois termes (sommants). Théorie Il existe une formule pour calculer la quantité
de sommants pour de telles partitions en fonction de n.
Curiosité Cette spirale hexagonale liste toutes les
quantités successives de ces partitions: nombres en bleu. 1, 2, 3, 4, 55,
7, 8, 10, 12, 1410, 16, 19, 21, 24, 2715 … |
Une spirale simple représentative
de la partition des nombres en trois termes au plus
|
|||
|
Brèves associées |
>>>
Partitions
du nombre 200 |
>>>
Brèves Théorie – Index |
||
|
Pour en savoir plus |
>>>
Tripartitions |
>>>
Partitions – Index |
||
766. Triangles entiers |
|
|||
|
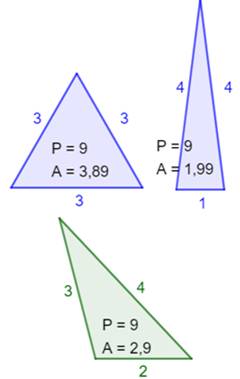
Triangle entier Un triangle entier est un
triangle dont les longueurs des côtés sont des nombres entiers. Tout triplet de
trois nombres entiers (a, b et c) est éligible à condition de respecter
l'inégalité triangulaire: a + b > c avec a et b les deux plus petites
longueurs.
En
conséquence, si n = a + b + c est le périmètre du triangle, toutes les
partitions de n sont éligibles sous la même condition. Pour le
nombre 9, trois telles partitions existent, soit
trois triangles entiers de périmètre 9.
|
Les trois triangles
entiers de périmètre 9
|
|||
|
Brèves associées |
>>>
Tripartitions
(ci-dessus) |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Triangles entiers |
>>>
Inégalité triangulaire |
||
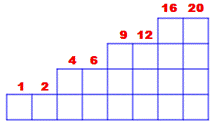
767. Produit, pizza et escalier |
|
|||
|
Produit Bipartition de n: sommes de deux nombres =
n. Quel est
le produit maximum de toutes les bipartitions des nombres ? Exemples
Pizza
Exemple avec 4 coupes, n = 6 et la suite donne Q
= 9, comme le montre aussi la figure. Escalier Cette suite est aussi la quantité de blocs au
rang n + 1 dans un escalier
progressant par double-marche. Pour n = 8 rangs, on a 20 blocs (petits carrés),
confirmé au nombre n°9 de la suite. |
Suite des produits maximums 0, 1, 2, 4, 6, 9,
12, 16, 20, 25, 30, 36, 42, 49, … = plancher (n² / 4)
|
|||
|
Brèves associées |
>>>
Points
dans le carré |
>>>
Brèves Dénombrement – Index |
||
|
Pour en savoir plus |
>>>
Bipartition et produit maximum |
>>>
Nombre pizza |
||
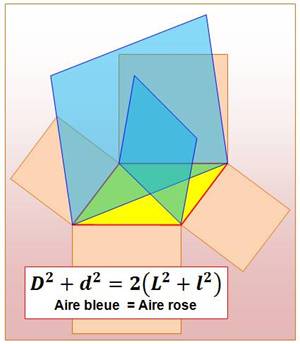
768. Règle du parallélogramme |
|
|||
|
Construction Un parallélogramme quelconque
(jaune). Les quatre carrés (roses)
construits sur ses côtés (L et l) et Règle
du parallélogramme Somme des
aires des carrés sur les côtés = somme des
aires des carrés sur les diagonales. Plus
simplement (moins imagé) Dans un
parallélogramme, la somme des carrés des côtés est égale à la somme des
carrés des diagonales. L²+ l² + L² + l² = 2
(L² + l²) = d² + D² |
Illustration
|
|||
|
Brèves associées |
>>>
Parallélogramme
divisé – Aire |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Règle du parallélogramme |
>>>
Parallélogramme, toutes les formules |
||
769. Intégrale amusante: ln et exp |
|
|||
|
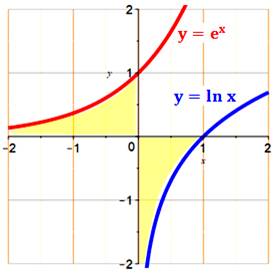
Propriétés Les
graphes des fonctions y = exp(x) et
y = ln(x) sont symétriques. La dérivée
de l'exponentielle est égale à elle-même, de même pour l'intégrale. Aire sous les courbes Les aires
montrées en jaune sont égales (en valeur absolue) et elles correspondent aux
intégrales:
Comment
les calculer ? Celle avec l'exponentielle est la plus simple. En effet:
|
Graphe
Chacune des aires sous courbe (en
jaune) vaut 1
|
|||
|
Brèves associées |
>>> Volume maximum de la boite |
>>>
Brèves Analyse – Index |
||
|
Pour en savoir plus |
>>>
Calcul intégral >>>
Fonction exponentielle |
>>>
Nombre 1 |
||
770. Calcul trigonométrique: cosinus |
|
|||
|
Montrer
que
Outils Relations sur la somme des
angles:
Vérification
avec Maple (Pour info) L'instruction combinée à
utiliser: combine(simplify(convert(convert(expand(E), tan), sincos))) |
Calcul
de E
Différence de ces deux
expressions:
Calcul
de F Même type de
calcul avec la somme:
|
|||
|
Brèves associées |
>>> Sinus
et cosinus en puissance 4 |
>>>
Brèves Trigo – Index |
||
|
Pour en savoir plus |
>>>
Relations trigonométriques >>>
Somme d'angles en Pi/k |
>>>
Trigo en première >>>
Trigo avec Maple |
||
771. Crible de Moessner |
|
|||
|
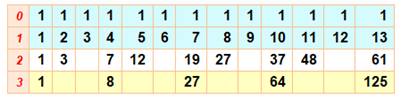
Construction des puissances des
nombres Le procédé est valable pour produire les
puissances des nombres par simple remplissage d'un tableau au prix de
sommations ciblées. Après avoir rempli la première ligne avec des
"1", on calcule la deuxième ligne en faisant simplement l'addition
du nombre du haut avec celui de gauche. Cette opération est répétée pour la ligne
suivante en ignorant un nombre sur k pour calculer la puissance kième. Même chose pour les lignes suivantes, en ignorant
un nombre supplémentaire. Des triangles se forment et le procédé s'arrête à
complétion de ces triangles. |
Le triangle des cubes
Ligne 0: suite de
"1". Ligne 1: somme des nombres
"au-dessus" + "à gauche". Ligne 2: même type de sommes
en ignorant un nombre sur trois. Ligne 3: sommes poursuivant
la construction de ces sortes de
triangles, donc en ignorant un nombre supplémentaire. Arrêt lorsque les triangles
sont complets. En l'occurrence, les nombres du bas sont les cubes
des nombres entiers successifs. |
|||
|
Brèves associées |
>>>
Procédé de Kaprekar |
>>>
Brèves Itération – Index |
||
|
Pour en savoir plus |
>>>
Crible de Moessner |
>>>
Cribles – Index |
||
772. Problème de Josèphe |
|
|||
|
Historique
(légende ?) Josephus Flavius
est un historien juif du premier
siècle (v.34-v100). Il est prisonnier des Romains dans une cave de
Yodfat (nord d'Israël actuel) avec
quarante soldats. Ceux-ci préfèrent
se suicider plutôt que de se rendre. Décision est prise que chacun tuera le
troisième à sa gauche et le dernier le fera lui-même. Josephus, ne
voulant pas mourir, trouva la place à occuper pour être le dernier. En
l'occurrence, la place 31. Notoriété Ce problème a
été exploité sous diverses formes par les créateurs d'amusements
mathématiques. Sa résolution
par récurrence est un sujet classique de programmation. |
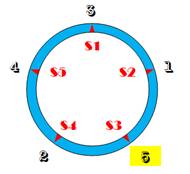
Cinq soldats sont rangés en cercle (S1, S2, S3,
S4 et S5). Ils doivent être exécutés les uns après les
autres en épargnant un soldat sur deux jusqu'à ce qu'il n'en reste qu'un
seul. L'un d'eux est désigné pour être épargné. Mais, à
lui de choisir la bonne place. Solution En périphérie du cercle, les nombres indiquent
l'ordre d'exécution: S2, S4, S1, S5 et S3.
Le soldat en position 3 sera sauvé. |
|||
|
Brèves associées |
>>> Grenouilles sauteuses |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Problème de Josèphe |
>>>
Les gardes du fortin |
||
773. Nombre 2 187 |
|
|||||
|
Le nombre 2 187 est la puissance septième de 3. 2 187 = 3 × 3 × 3
× 3 × 3 × 3 × 3 = 37 Avec cette propriété, ce nombre n'ayant aucune
composante en puissances inférieures à 7, s'écrit: 10 000 000 en ternaire
(base 3). Quelques opérations remarquables:
|
Somme qui possède les mêmes chiffres que le terme
ajouté à 2187.
Martin
Gardner |
|||||
|
Brèves associées |
>>> Nombre 1 729 – Somme de cubes |
>>>
Brèves Nombres – Index |
||||
|
Pour en savoir plus |
>>>
Nombre 2 187 (DicoNombre) |
>>>
Numération ternaire |
||||
774. Calcul de sommes d'inverses (1) |
|
|||
|
Exemple:
calculez (avec astuces !)
On remarque que, par exemple:
En appliquant à toutes les fractions:
|
Propriété
Formule
générale
Exemple
|
|||
|
Brèves associées |
>>> Somme des inverses |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Somme de d'inverses de produits |
>>>
Sommes d'inverses |
||
775. Calcul de sommes d'inverses (2) |
|
|||
|
Exemple:
calculez (avec astuces !)
On remarque que, par exemple:
En appliquant à toutes les fractions:
|
Propriété
Formule
générale
Exemple
|
|||
|
Brèves associées |
>>> Somme des inverses des carrés |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Somme de d'inverses de produits |
>>>
Sommes d'inverses |
||
776. Zéros et puissances de 10 |
|
|||
|
Puissances de 10 Les puissances de 10 sont le produit de deux
facteurs: 10k = 2k × 5k. Parmi elles, quelles sont celles dont les deux
facteurs sont sans "0" ? Il en existe seulement dix: (Voir tableau). Puissances de 2 Les puissances {10, 11, 12, 17, 20, 21, 22, 23,
…} contiennent des "0". Puissances de 10 À partir de 33, toutes les puissances de 5
contiennent un "0". |
Puissances de 10 sans "0"
dans ses facteurs 10 = 2 × 5 102 = 4 × 25 103 = 8 × 125 104 = 16 × 625 105 = 32 × 3 125 106 = 64 × 15 625 107 = 128 × 78 125 108 = 256 × 390 625 109 = 512 × 1 953
125 1010 = 1 024 × 9 765
625 1011 = 2 048 × 488 28
125 1012 = 4 096 × 244 140 625 1013 = 8 192 × 1 220 703 125 1014 = 16 384 × 6 103 515 625 1015 = 32 768 × 305 17 578 125 1016 = 65 536 × 152 587
890 625 1017 = 131 072 × 7 629
394 53 125 1018 = 262144 × 3 814
697 265 625 ... 1033 = 8 589 934 592 ×
116 415 321 826 934 814 453 125 |
|||
|
Brèves associées |
>>> Opérations avec les chiffres |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Puissances de 10 >>>
Puissances de 2 |
>>> Nombre 10 |
||
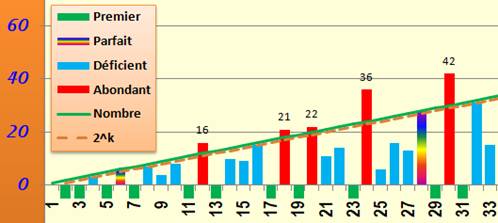
777. Nombres de 1 à 33Déficients, parfaits ou abondants |
|
|||
|
Propriété des nombres face la somme de leurs
diviseurs stricts (sans compter le nombre lui-même). La droite verte représente les nombres. En bleu, les nombres avec somme inférieure, les
nombres déficients. En rouge, les abondants. En arc-en-ciel, les nombres parfaits. Sur la droite pointillée, les puissances k de 2;
leur somme des diviseurs vaut 2k – 1, un nombre de Mersenne. |
|
|||
|
Brèves associées |
>>> Diviseurs |
>>> Brèves
Fonctions Arith. – Index |
||
|
Pour en savoir plus |
>>>
Tables des nombres déficients … >>>
Nombres parfaits |
>>>
Puissances de 2 >>>
Nombres de Mersenne |
||
778. Manipulation de polynômes |
|
|||
|
Défi Trouver la valeur de l'expression à la puissance
4, connaissant les deux autres. On ne demande pas de calculer les valeurs de a, b
et c. Comment s'y prendre ? |
|
|||
|
Solution
|
||||
|
Brèves associées |
>>>
Équation 5x–1 – 2x = 0 |
>>>
Brèves Équations – Index |
||
|
Pour en savoir plus |
>>>
Calcul avec polynômes de degré 4 (Ce problème et
un plus difficile …) |
>>>
Équations – Index >>>
Identités remarquables |
||
779. Théorème de Pythagore – Réciproque |
|
|||
|
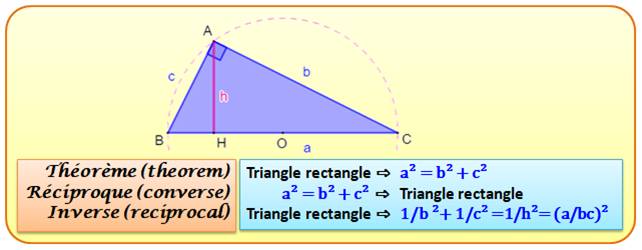
Trois visions du théorème de Pythagore
|
||||
|
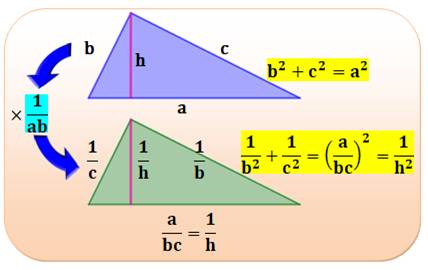
Démonstration visuelle de l'inverse du théorème
de Pythagore Triangle rectangle du haut: le cas classique du
théorème de Pythagore. Toutes les mesures sont divisées par ab pour
obtenir le triangle rectangle du bas. Le théorème de Pythagore s'applique aux nouvelles
mesures. La relation ah = bc qui donne h en fonction de a,
b et c dans le triangle rectangle complète l'égalité. |
Deux triangles semblables dans un rapport 1/ab
|
|||
|
Brèves associées |
>>>
Théorème de Pythagore |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème de Pythagore >>>
Triangle rectangle – Relations |
>>>
Théorème de Thalès >>>
Homothétie |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()