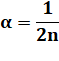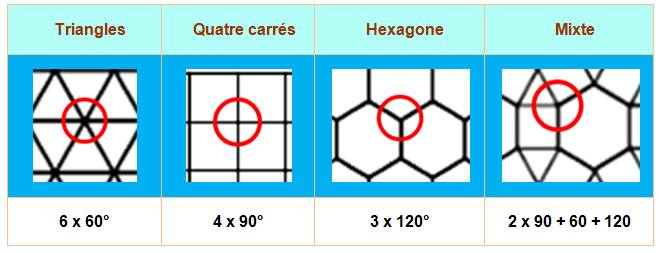
Polygone et pavage

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/02/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Pavage
Débutants Pavage	du PLAN				Glossaire Général
INDEX Géométrie	Approche	Avec polygones	Apériodique	Pavage fini
	Triangles	Carrés parfaits	Rectangles	Penrose (losanges)
	Pentagone	Hexagone	Dodécagone	Disque (Pizza)
	Dominos	Échiquier	Plus Plus (Jeu)	Sphinx
		Sommaire de cette page >>> Point sur le pavage polygonal >>> Pavage – Définition >>> Trois pavages du plan avec polygones réguliers >>> Pavage hexagonal de l'écolier >>> Polygones réfléchis >>> Vocabulaire >>> Anglais

Pavage POLYGONAL

Pavage du plan avec des polygones

Trois possibilités seulement avec des polygones réguliers >>>

Nombreuses possibilités en combinant les polygones >>>

Autres possibilités avec des polygones irréguliers >>>

Anglais: Tessellation

Devinette

Faire une croix avec ces six pièces;

ou encore, faire la lettre V.

Solution

Le point en matière de pavage polygonal

On peut paver une surface plane (infinie) avec les formes géométriques suivantes:

triangle quelconque,

quadrilatère quelconque,

trois types d'hexagones convexes, et

quinze types de pentagones convexes (irréguliers).

Mais c'est impossible avec des:

polygones de plus de six côtés,

pentagones réguliers (108° incompatible avec 360°).

Il existe de nombreux types de pavages en mixant les formes régulières ou irrégulières.

En 1918, Karl Reinhardt a montré que tous les triangles et quadrilatères pavent le plan, qu'il n'existe que 3 types d'hexagones qui permettent de réaliser un pavage et qu'un polygone à sept côtés ou plus ne permet pas de recouvrir un plan.

En 2017, Michaël Rao a montré qu'il n'existe que 15 pavages pentagonaux possibles.

Voir Pavage pentagonal / Polygones réguliers

Pavage
Le pavage d'un plan, à la manière d'un puzzle infini, doit recouvrir toute la surface sans trou ni chevauchement.	Condition pour les formes assemblées à un sommet: la somme des angles doit être égale à 360°.
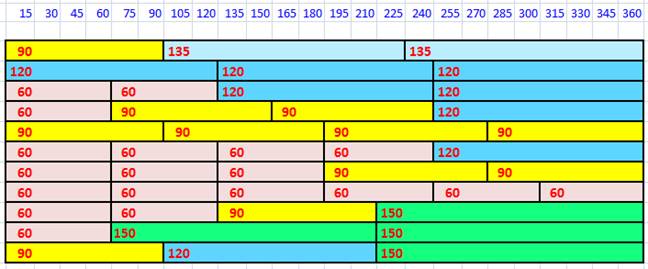
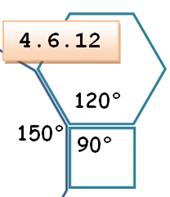
Somme des angles au sommet = 360° Les onze possibilités de pavage semi-régulier Triangle, carré, hexagone, octogone et dodécagone pour lesquels tous les sommets sont du même type. Exemple: la dernière ligne indique que le sommet est formé des sommets d'un carré (90°), d'un hexagone (120°) et d'un dodécagone (150°). Total 360° (Illustration) Notation: chaque polygone est noté par son nombre de côté. La dernière ligne donnera: 4.6.12. (Illustration). La première sera 4.8². Présentation: Chaque ligne du tableau peut faire l'objet d'un ou plusieurs types de pavage. Ainsi, la septième ligne donne: 3³.4² qui a pour sommet trois fois un triangle (3³) suivi de deux fois un carré (4²). Mais, avec la même combinaison, on peur aussi réaliser: 3².4.3.4 qui correspond à deux triangles, un carré, un triangle, un carré (voir modèles). Généralisation: Il existe d'autres pavages en mixant des sommets de plusieurs types. En 1987, Grünbaum et Shephard donnaient une liste de 20 pavages semi-réguliers (2-uniform demiregular tilings) à sommet unique ou multi-sommet (voir modèles).

Douze exemples de pavages semi-réguliers avec notation de chacun

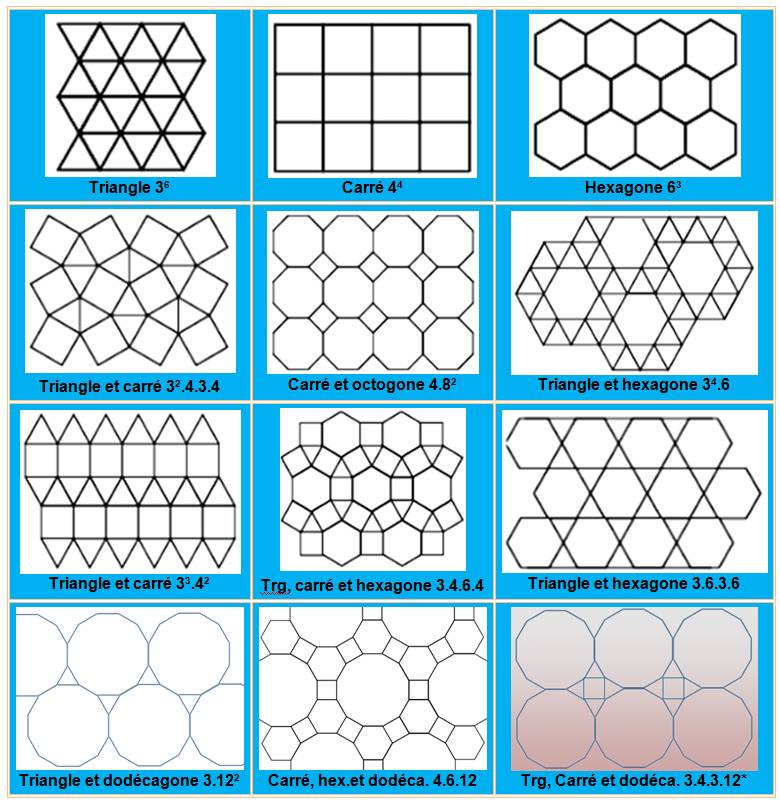
Un exemple de pavage semi-régulier à deux types de sommet (3.4.6.4 et 3²4.3.4)

Pavages impossibles avec les polygones réguliers avec n = 5 ou n > 6

Exemples de pavages

Trois pavages du plan avec des polygones
CARRÉS
TRIANGLES équilatéraux
HEXAGONES réguliers Note: l'hexagone peut être découpé selon diverses formes à son tour. Un exemple ci-dessous.

Pavage hexagonal d'écolier

Pouvez-vous voir le relief des cubes de deux manières différentes?

Escaliers montants vers la droite avec le plat des marches en bleu, ou

Escaliers montants vers la gauche avec le plat des marches en orange.

Voir Illusions

Exemple de pavage particulier avec des losanges (deux types)

Voir Losange (Penrose)

Polygones réfléchis
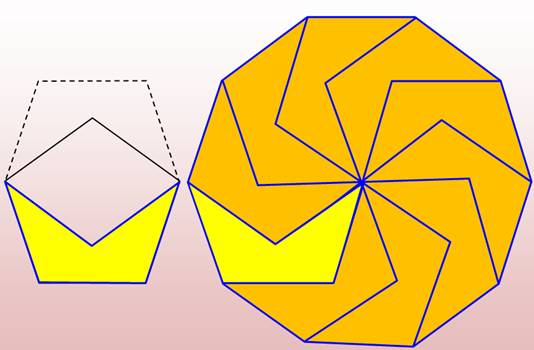
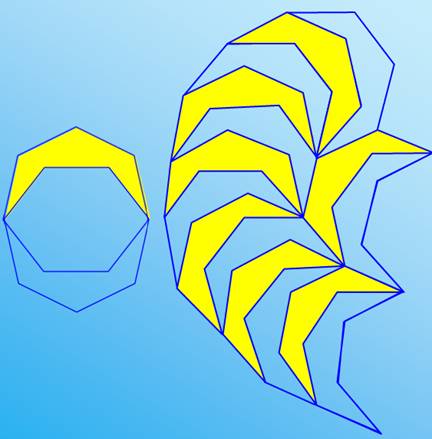
Une méthode générale de pavage du plan consiste à utiliser des polygones réfléchis. Ici, le pentagone dont une partie est repliée sur lui-même le long d'une ligne passant par deux sommets. La tuile jaune est utilisée pour paver le plan. Cette méthode est valable pour tout polygone ayant un nombre impair de côté, supérieur à 3.	Un pentagone réfléchi régulier sert de tuile pour paver un décagone régulier. Le pavage peut être étendu à tout le plan.
Cas de l'heptagone et son réfléchi (à gauche). Une idée du pavage qu'il est possible de réaliser (à droite). L'angle aigu du polygone réfléchi à n côté est égal à: Pentagone réfléchi: 36 ° Heptagone réfléchi: 25,714 …°

Anglais pour tuile: tile (tuile) ou aussi shield qui veut dire bouclier, écu, blason

Devinette – Solution

Retour

Vocabulaire
Polygone régulier Polygone irrégulier	Polygone dont les côtés sont tous égaux. Dans le cas contraire, ils sont irréguliers (ou quelconque).
Polygone convexe	Les droites portant les côtés sont toutes externes au polygone (aucune de possède de segment interne au polygone).
Angle (intérieur) du polygone	Angle donnant vers l'intérieur du polygone. D'une manière générale la somme des angles intérieurs d'un polygone vaut: S = (n – 2) x 180, avec n le nombre de côtés. L'angle intérieur pour un polygone régulier vaut alors: A = S / n. Ex. Pour n = 6 (hexagone): S = 4 x 180 = 720° et, pour l'hexagone régulier: A = 720 / 6 = 120°.
Formes congruentes	Autre terme pour dire superposables (ou égales).
Plan (surface plane)	Ce qui est plat, à deux dimensions, comme la surface d'une table. Le problème du pavage suppose que la surface est infinie. Comme pour carreler une pièce il faut sectionner des carreaux; un exemple de dessin de pavage montrera des formes tronquées.

Voir DicoMot Maths

English corner

A tessellation is created when a shape is repeated over and over again to cover the plane without any overlaps or gaps.

A vertex of a tessellation is a point where three or more corners of the tessellating shapes are joined.

A tessellation can be defined as the covering of a surface with a repeating unit consisting of one or more shapes in such a way that:

there are no spaces between, and no overlapping of, the shapes thus employed, and

the covering process has the potential to continue indefinitely (for a surface of infinite dimensions).

Voir Anglais

Suite	Pavage avec pentagones Jeu du PLUS PLUS
Voir	Carré Carrés parfaits Construction géométrique des nombres Dodécagone Dominos Frises – Bandes décoratives Géométrie – Index Golygone à huit côtés	Hexagone – Généralités Hexagone – pavage Méandres Pavage mystérieux du triangle Pavage finis – Nombre de Heesch Pentominos Poincaré Polygone Triangle équilatéral
Diconombre	Nombre 3 Nombre 6 – hexagone
Sites	Il n'existe que 15 pavages pentagonaux possibles – CNRS – 29 septembre 2017 Tessellation Tutorials – Suzanne Alejandre – Très complet! Shapes that tesssellate – Illustrations de nombreuses possibilités; possibilité de créer votre propre pavage. The mathematcis of tesselation – Andrew Harris – 2000 Demiregular tiling – Wikipedia – Tous les pavages et liens vers d'autres sites cherchant l'exhaustivité. Tiling – Jaap Scherphuis – Une grande quantité de pavages, sinon tous, avec applet pour créer les vôtres.
Cette page	http://villemin.gerard.free.fr/Pavage/Polygone.htm