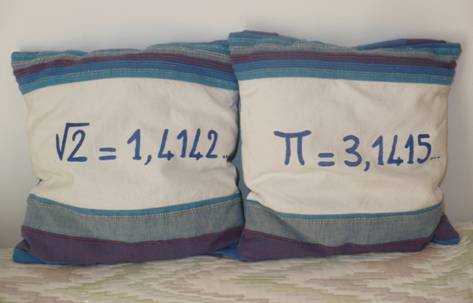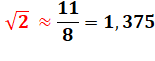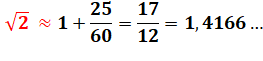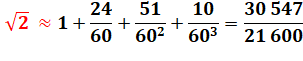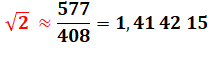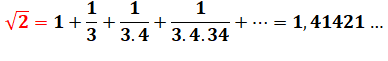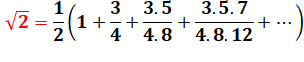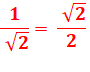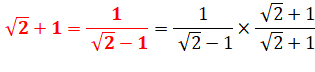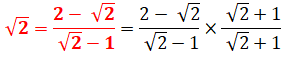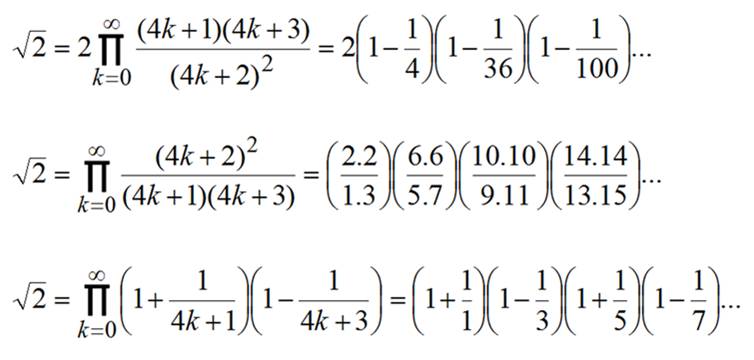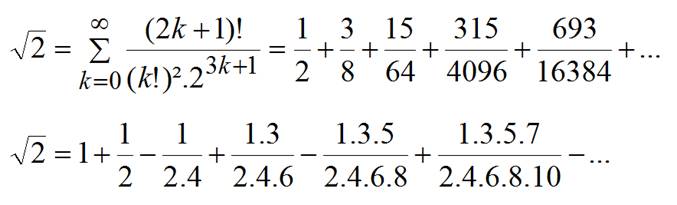|
||||||||||||||||||||||||||||
![]()
Valeur en bref
|
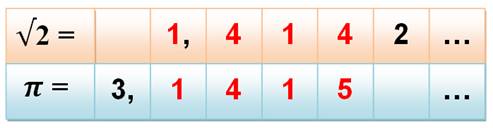
Valeur facilement mémorisable pour
les quatre premières décimales:
|
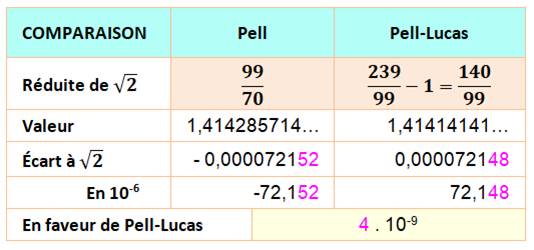
Une fraction proche de racine de 2: 99
/ 70 = 1, 4142 857… |
|
Cent premières décimales 1, 4142135623
7309504880 1688724209 6980785696 7187537694 8073176679
7379907324 7846210703 8850387534 3276415727 … Depuis
juin 2016, ce nombre est connu avec 10 000 milliards de décimales (Ron Watkins). |
|
Voir Explication du motif 11 14 21 35 dans racine de 2
|
Deux
constantes remarquables, qui nous offrent des analogies:
|
VALEURS
exacte et approchées de racine de 2

|
|
Diagonale du
carré de côté 1. |
|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
||
|
= 1,414 215 5 |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
= 0,707 106 = sin 45° = cos 45° |
||
|
|
|
|
|
|
|
|

|
|
||
|
Due à Bombelli
(1572) |
|
|
|
Notation
concise |
|
|
|
Autre
valeurs |
|
|
Voir Application à la résolution de l'énigme
du numéro de la villa
|
|
|
|
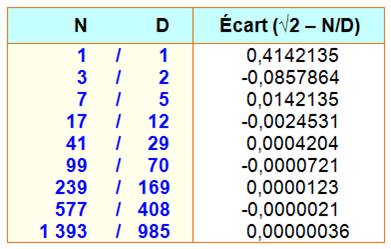
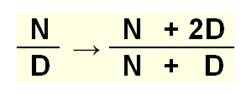
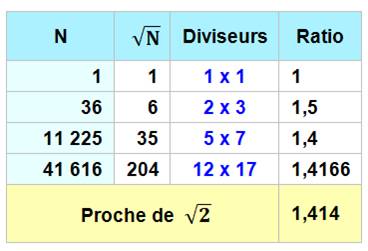
FORMULES ITÉRATIVES donnant les mêmes fractions (réduites)
Propriétés
En
fait:
N² – 2D² = Réduites avec Pell-Lucas
|
|
Voir Tables
|
|
|
|
Les identités (2) et (3) sont identiques, l'une étant
le développement de l'autre. Voir
explications en Identités
en k Ces
formules sont très lentement convergentes vers racine de 2.
|
|
|
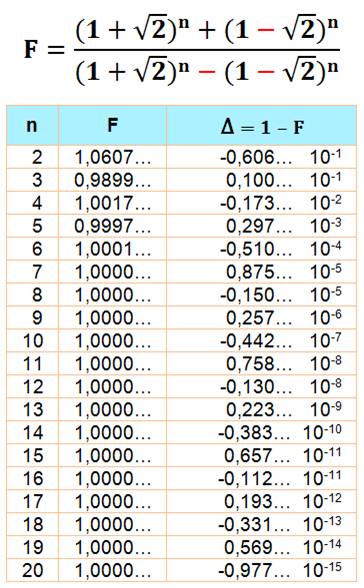
Formule convergente vers 1
avec racine de 2 |
|
|
|
|
Voir Nombres de Fibonacci et formule de
Binet
|
Formule convergente vers 1
avec racine de 2 |
|
|
|
|
|
|
|
|
|
|
|
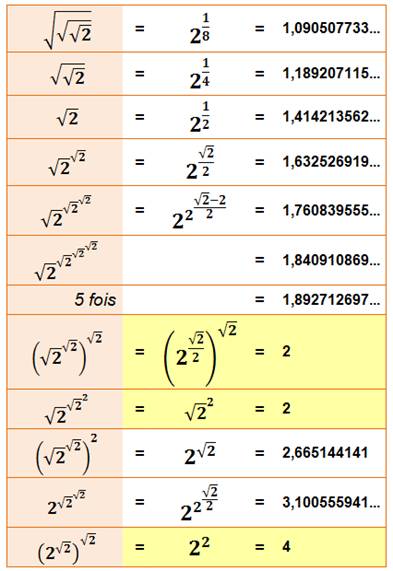
Tableau des racines énièmes de 2 pour n de 2 à 20 avec 30 chiffres significatifs
|
Voir Calcul des racines avec calculette / Tables de valeurs numériques
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Diconombre |
|
|
Livre |
|
|
Site |
|
|
Cette page |
![]()