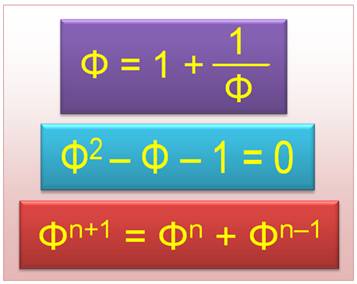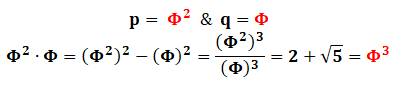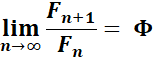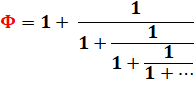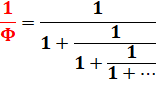|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre d'or – FORMULES
|
|
Quels sont
deux nombres p et q dont:
sont tous égaux ? Solution
|
Voir Brève 57-1123 / Nombre Phi3 = 4,236…
|
|
||
|
x²
– x – 1 = 0 x2 – x1
– x0 = 0 |
|
|
|
1 / Φ = Φ - 1 Φ = 1 + 1 / Φ Φ 2 = Φ + 1 Φ 3 = 2 Φ + 1 = ( Φ + 1) / ( Φ - 1) |
|
|
|
x4
– 2x3 + x2 – 1 =
(x² – x – 1)(x² - x + 1) = 0 |
|
|
Voir Équation
trigonométrique en or / Nombre
d'or et théorème de Ptolémée
Résolution d'un équation étonnante
dont la racine est le nombre d'or
|
|
||
|
|
|
|
|
|
||
|
Φ = [1 ; 1, 1, 1, 1, 1...] |
|
|
|
1/ Φ = [0 ; 1, 1, 1, 1, 1...] |
|
|
|
|
|
|
Voir Table des fractions
continues de Phi / Racines
continues de Phi / Fractions - Glossaire
Phi et fractions continues de
Rogers-Ramanujan
|
|
|
|
Fractions d'approximation du nombre d'or appelées réduites du
nombre d'or =
quotient de deux Fibonacci consécutifs &
présentation de la fraction continue
correspondante. 1 1 2 2 3/2 1+1/`2` 5/3 1+1/(1+1/`2`) 8/5 1+1/(1+1/(1+1/`2`)) 13/8 1+1/(1+1/(1+1/(1+1/`2`))) 21/13 1+1/(1+1/(1+1/(1+1/(1+1/`2`)))) 34/21 1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))) 55/34
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))) 89/55
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))))) 144/89
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))))) 233/144 1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))))))) 377/233
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))))))) 610/377
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))))))))) 987/610
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))))))))) 1597/987
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))))))))))) 2584/1597
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))))))))))) 4181/2584 1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`))))))))))))))) 6765/4181
1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/`2`)))))))))))))))) |
|
Voir Approximation
de Phi
|
|
|
|
Chaîne dorée
Construction
Itération: Sn = concaténation
de Sn-1 et de Sn-2 Valeurs de la chaîne
dorée 0 1 10 101 10110 10110101 1011010110110 101101011011010110101 ... Propriétés
|
|
|
|
||
|
Voir Page spéciale Voir Pentagone |
||
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrForm.htm |
![]()