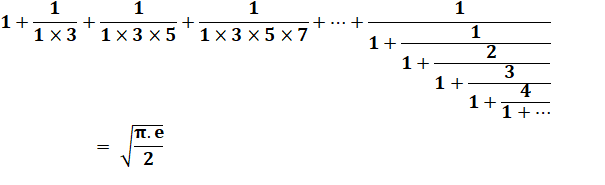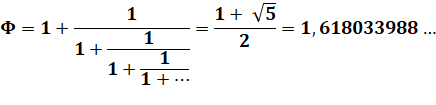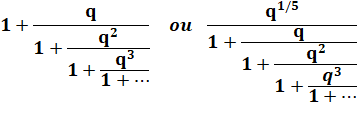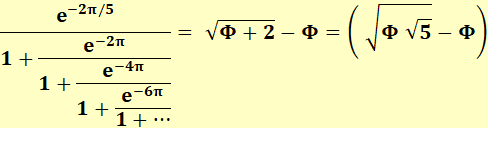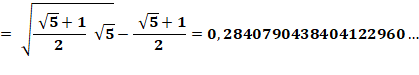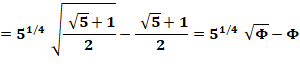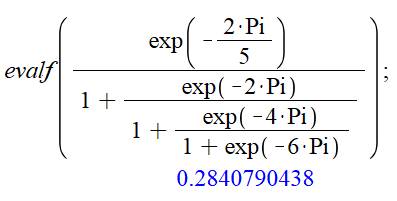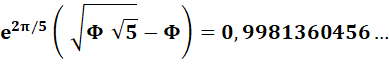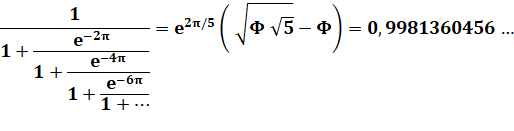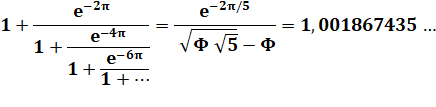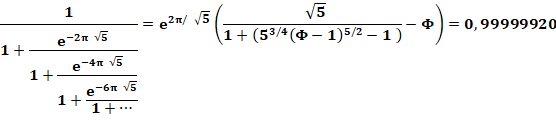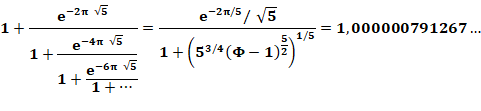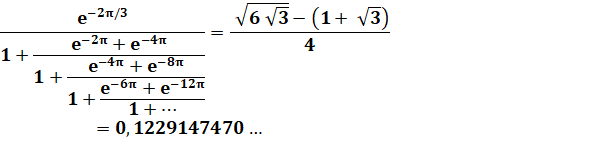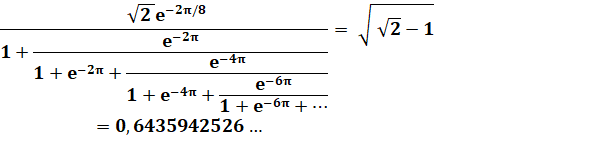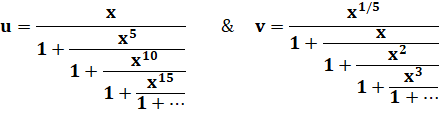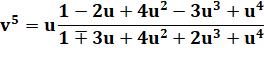|
||||||||||||||||||||||||||||||
![]()
|
FRACTIONS CONTINUES du type Rogers-Ramanujan Une belle formule due à Ramanujan, puis Exemples d'application des fractions continues de
Rogers-Ramanujan. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Relation entre les nombres naturels
et les nombres impairs
Notons N1 et N2 les deux parties de
gauche: C = N1 + N2 = 2, 066 365
676 ... Quelques valeurs
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
||
|
Fraction
continue classique du nombre d'or |
|
|
|
Fraction continue
générale de Rogers-Ramanujan |
|
|
|
Fraction
continue de Ramanujan impliquant Phi, le nombre d'or Voir Autres fractions continues de Phi |
Formule
Évaluation avec Maple avec seulement
quatre étages
Note: nombre presque entier
Voir Ce nombre
dans le Diconombre |
|
|
Formulations voisines mettant en évidence des nombres presque entiers |
|
|
Meilleures approximations de l'entier en introduisant racine de 5 |
|
Source: Wolfram Mathworld
|
|
|
|
|
|
|
|
|
|
Alors
La
formule est d'autant plus précise que u est grand ou alors que la quantité de
termes (d'étages) est grande. Dit-autrement, la formule ne converge pas vite. |
|
Historique
|
Ces
identités figuraient sur la lettre envoyée par Ramanujan à G.H. Hardy en
1913. Voir Historique |
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()