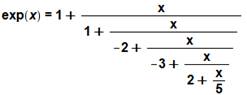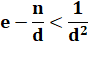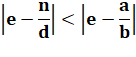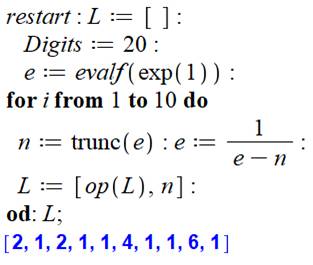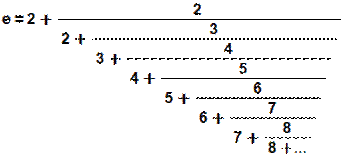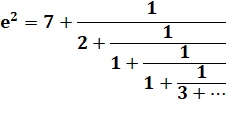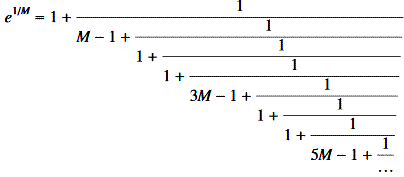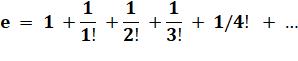|
Édition du: 24/09/2021 |
|
INDEX |
Exponentielles |
|||
|
Dévelop ex |
||||
![]()
|
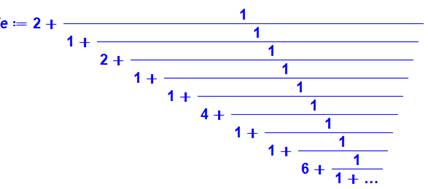
FRACTIONS EXPRIMANT "e"
La troisième fraction n'est par une réduite, mais
sa forme palindrome est facile à
retenir. |
||
|
|
Sommaire de cette page >>>
Fractions continues et réduites de e >>>
Calcul de la fraction continue de e >>>
Exemple de calcul d'une réduite >>>
Table des réduites >>>
Une autre fraction continue notable >>>
Fractions "factorielles" >>>
Fractions progressives >>>
Comparaison |
Débutants Glossaire |
Voir Mnémotechnique
– Retenir les chiffres de e
|
Forme développée Les dix premiers termes de la fraction
continue. Pour info
|
|
|
|
Forme abrégée de
la fraction continue Les cent premiers termes Notez
la régularité de la progression des termes. Le
nombre e est irrationnel car son
développement en fraction continue est infini. |
e = [2, 1, 2, 1, 1, 4,
1, 1, 6, 1, 1, 8,
1, 1, 10, 1, 1, 12,
1, 1, 14, 1, 1, 16,
1, 1, 18, 1, 1, 20,
1, 1, 22, 1, 1, 24,
1, 1, 26, 1, 1, 28,
1, 1, 30, 1, 1, 32,
1, 1, 34, 1, 1, 36,
1, 1, 38, 1, 1, 40,
1, 1, 42, 1, 1, 44,
1, 1, 46, 1, 1, 48,
1, 1, 50, 1, 1, 52,
1, 1, 54, 1, 1, 56,
1, 1, 58, 1, 1, 60,
1, 1, 62, 1, 1, 64,
1, 1, 66, 1, 1, …]
Lecture: e est égal à la fraction continue dont le
premier terme est 2 suivi indéfiniment de triplets dont les termes centraux
sont les nombres pairs successifs et les deux autres sont 1. Autre écriture qui généralise l'écriture en 1, 2k, 1. Le 2 est remplacé par 1, 0, 1 e = [1, 0, 1,
1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, …] |
|
|
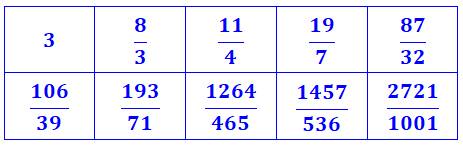
Réduites de e Les dix plus
petites valeurs. Les réduites
sont les fractions obtenues en calculant la fraction à chaque ajout d'un
étage supplémentaire. Anglais: convergents. |
|
|
|
Intérêt des réduites Avec la réduite, il n'est pas possible de trouver une meilleure
approximation ayant un dénominateur plus petit. |
Théorème de la meilleure approximation rationnelle Une
réduite est la "meilleure approximation" d'un nombre irrationnel.
Elle vérifie:
Autre formulation:
pour toute fraction a/b avec b ≤ d:
On
ne retrouve l'égalité que pour a = n et b = d. |
|
|
Méthode |
Conserver la valeur entière du nombre. Isoler la partie décimale du nombre. Calculer son inverse, lequel devient le nombre Recommencer. |
||
|
Calcul
|
|||
|
Programme (Maple)
|
But Calculer la liste des termes de la fraction
continue de la constante e. Commentaires Initialisation. Déclaration d'une liste vide L. Demande que les calculs soient effectués avec 20
chiffres significatifs (ne pas le faire, expose à des erreurs d'arrondis) Boucle avec dix itérations. Extraction de la valeur entière n de e (le
nombre). Calcul de l'inverse de la partie décimale du
nombre. Ajout du nouveau terme n dans la liste L. édition de la liste L en bleu. |
||
Voir Calcul du PGCD
par l'algorithme d'Euclide
Exemple de calcul d'une réduite
|
|
On trouve parfois cette notation (plus
facile à imprimer)
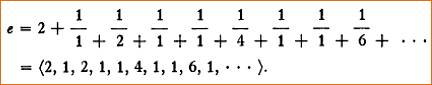
|
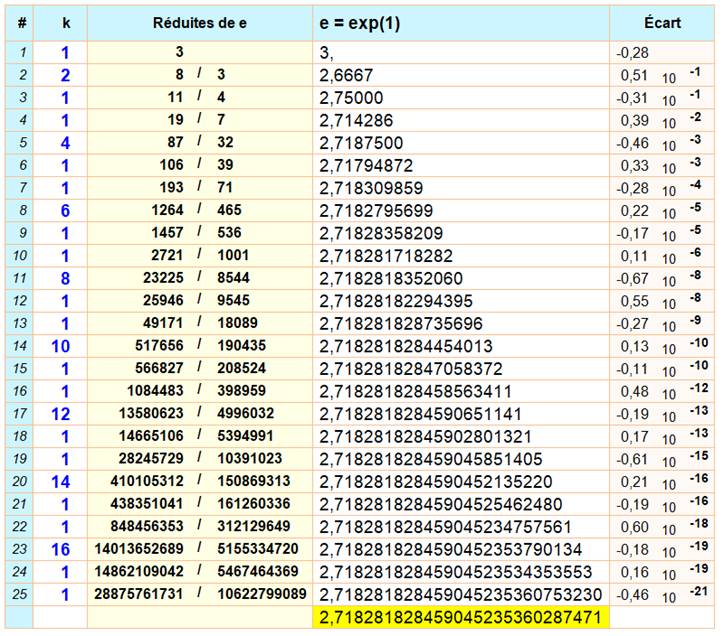
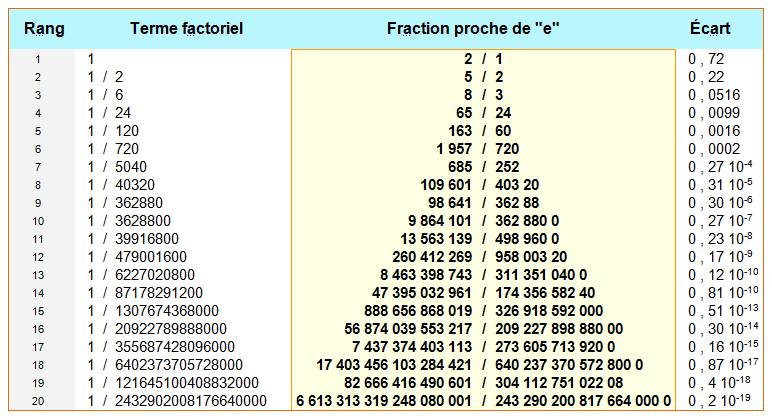
Tableau pour les 25 plus petites
réduites de e |
Exemple avec la ligne #
4: Le terme supplémentaire k dans la fraction
continue est 1. La réduite est la fraction 19/7 qui vaut 2,714286 … Son écart par rapport à la valeur exacte de e est
égale à 0,39 10-2 = 0,0039… |
|
|
|
||
Voir Réduites
d'autres constantes
Une autre fraction continue notable pour e et celle du carré de e
|
La valeur décimale de celle-ci est: 2,71828165… |
= [7, 2, 1, 1, 3, 18, 5, 1, 1, 6, 30, 8…]
|
Voir Autres fractions continues pour e
(moins simples)
Tout nombre M par Euler
|
Euler trouve cette fraction
continue applicable à tout nombre réel. Avec M = 1, on retrouve la fraction continue exprimant e. |
|
De
fractionibus continuis dissertatio – Euler
|
Expression en factorielle |
Calcul en utilisant la formule en exponentielles
et réduction au même dénominateur à chaque ajout
d'un terme. |
|
|
|
||
Voir Approche de "e" est irrationnel
|
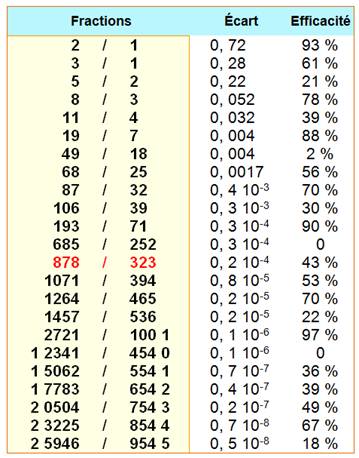
Fraction
proches de la valeur de e Les réduites sont les meilleures approximations
de e. Cependant nous allons recherche un algorithme de
calcul de fractions se rapprochant au maximum de la valeur de "e". Principe
de l'algorithme Recherche des fractions à dénominateurs
croissants pour lesquelles l'écart avec "e" diminue. Le dénominateur D étant donné, on calcule la
valeur entière de X = D . e. On essaie les deux fractions suivantes qui
encadrent "e": |
Programmation de
l'algorithme ECARTENREGISTRE:=10 pour D de 1 à
10 000 faire calculer
X = tronque (D . e) pour N de X à
X + 1 faire FRACTION:=
N / D ECART:= absolu( exp(1) – FRACTION ) si ECART < ECARTENREGISTRE alors imprimer (N, D) ECARTENREGISTRE:= ECART fin du si fin du pour fin du pour Voir Programmation |
|
|
Tableau
de valeurs
|
||
|
Méthode On compare les trois types de fractions obtenues. On les classe par écarts décroissants par rapport
à la valeur de "e". Exemple 878 / 323 est une fraction notable car formée
avec deux palindromes
|
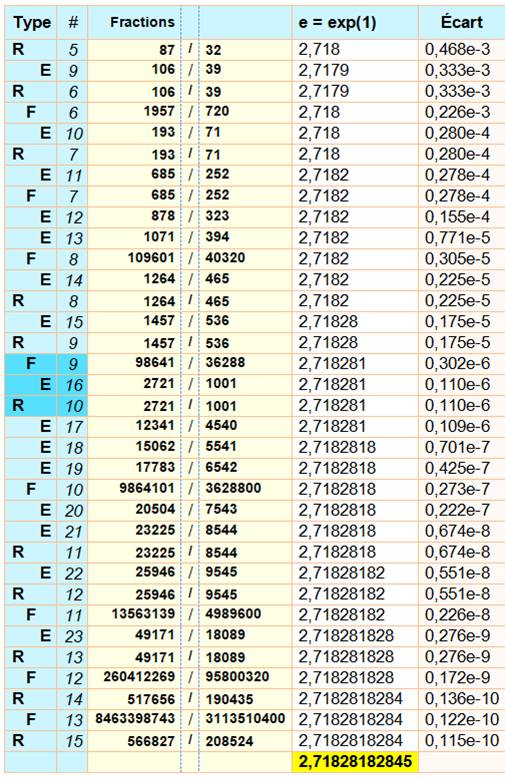
Lecture Type de
Fraction: R réduite; F avec les factorielles; E fraction approchée. Le rang pour
chaque type est en #. Fractions. Valeur décimale
tronquée aux chiffres exacts. Écart avec la
valeur exacte de e, laquelle valeur est rappelée en bas du tableau |
|
|
Tableau
de valeurs
Comparaison (trois
valeurs en bleu foncé) Comme le dit la
théorie, la réduite (R) issue de la fraction continue est la plus efficace,
la plus économe en quantité de chiffres. Avec un calcul d'écart minimum (E),
on retrouve souvent la réduite. Les valeurs obtenues avec les factorielles ne
sont pas particulièrement performantes. |
||
GRAND MERCI à Thierry de la Rue pour les
améliorations apportées à cette page
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()