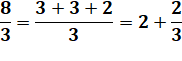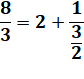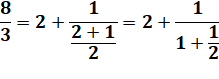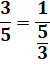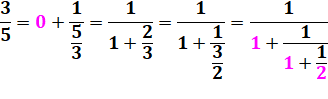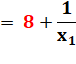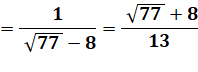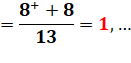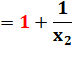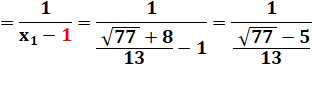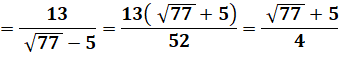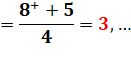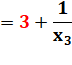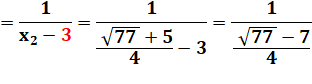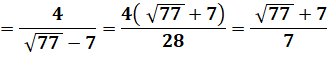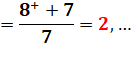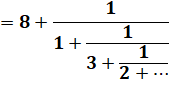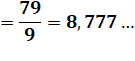|
||||||||||||||||||||||||||||||
![]()
|
FRACTIONS CONTINUES ou fractions à étages Moyen de décrire un nombre
décimal qui présente une analogie
avec la découpe d'un rectangle; qui ressemble au calcul du
PGCD; et qui permet de résoudre des
équations. |
|
|
|||||||||
|
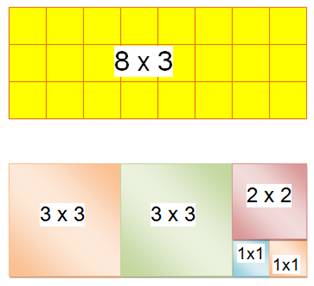
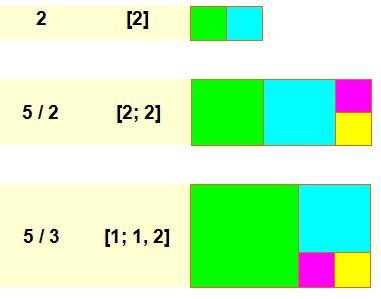
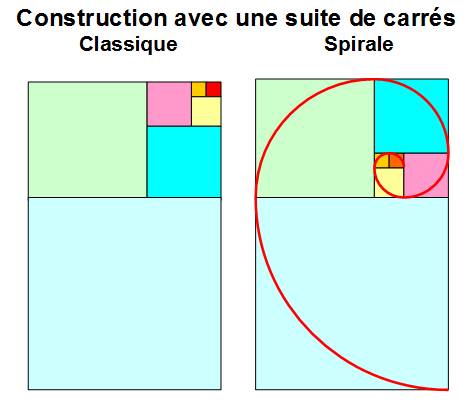
La découpe du rectangle |
|||||||||
|
|
||||||||
|
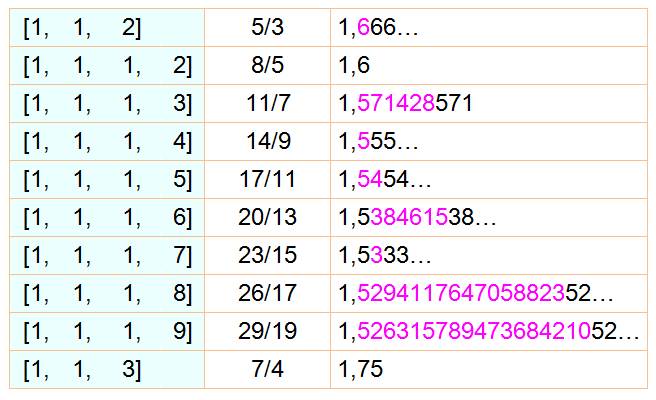
Passons aux fractions |
|||||||||
|
8
/ 3
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
[2;
1, 2]
|
||||||||
|
Notations
|
|||||||||
|
|
||
|
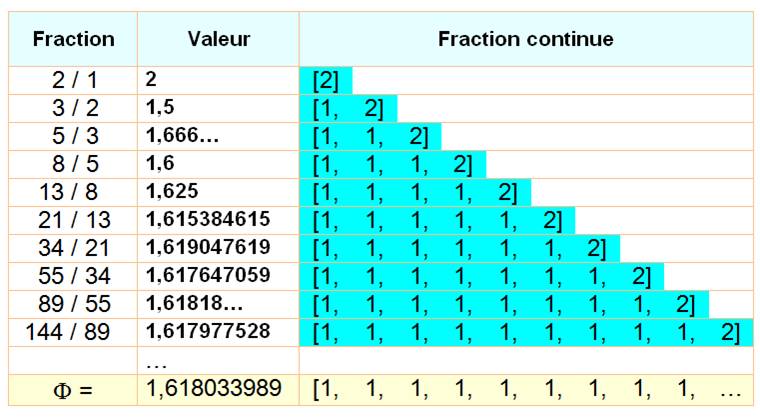
Quelques fractions simples
Et les petites fractions ( < 1) |
||
|
3 / 5
|
|
|
|
|
|
|
|
|
[0; 1, 1, 2]
|
|
|
[ 1; 1, 2]
|
|
|
|
|
|
|
|
|
|
|
|
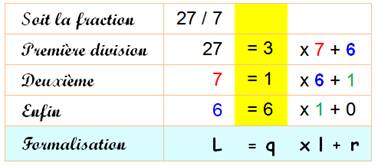
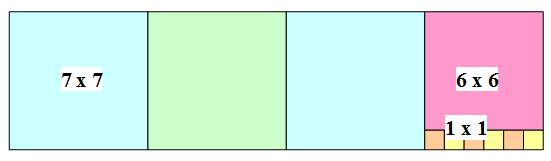
En jaune, on retrouve la
fraction continue: 27 / 7 = [3; 1, 6] L et l sont les dimensions des carrés formés dans
le grand rectangle de épart de 27 x 7.
Le
PGCD est la taille l du dernier carré Dans l'exemple ci-dessus: l = 1 et PGCD(27, 7) = 1 . 27 et 7 sont premiers
entre eux ( on dit aussi: étrangers).
|
|
|
|
|||
|
|
|||
Soit une racine
|
|
|
|
Sa valeur est
supérieure à 1 et inférieure à 2
|
|
= 1 + y
|
|
Exprimons y en fraction avec un dénominateur
supérieur à 1
|
|
= 1 + 1/x
|
|
Quelle est la
valeur de x ?
|
x
|
= 1 / (
|
|
En multipliant
par le conjugué
|
|
= (
|
|
Mais nous
connaissons la valeur de la racine de 2
|
|
= (1 + 1/x + 1)
= 2 + 1/x
|
|
On remplace x par
sa valeur chaque fois qu'il apparaît
|
x
|
= 2+1/(2+1/2+1/…
|
|
Nous avons notre
fraction continue et la valeur de
|
|
= [1; 2, 2, 2, 2…]
|
|
|
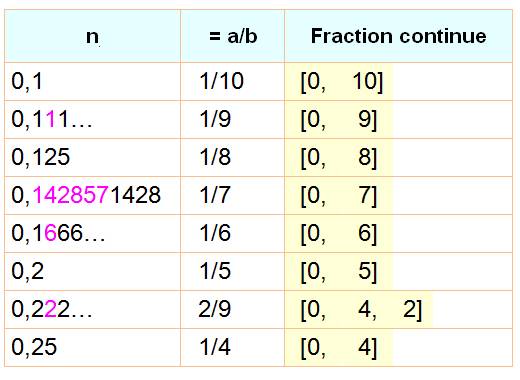
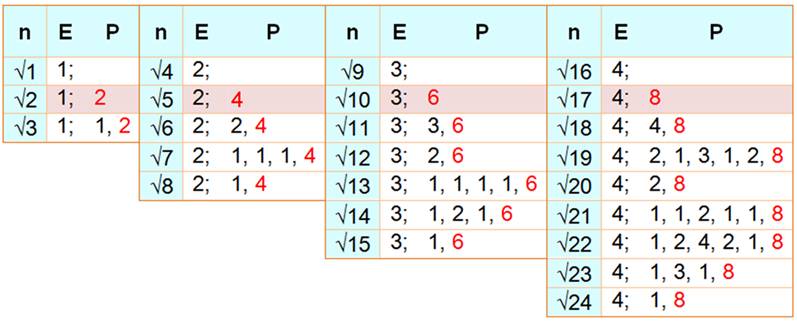
Racine carrée des premiers nombres E: entier:
valeur entière de la fraction continue
P: période:
chiffres qui se répètent indéfiniment
|
|
Calcul de la racine carrée d'un
nombre en
utilisant sa fraction continue |
|
||
Appliquons ce que nous venons de voir au calcul des racines carrées.
|
|||
Soit une racine.
|
|
= 8,7749…
|
|
Sortons le carré
le plus grand possible.
|
77
|
= 64 + 13
|
|
Premier étage de
la fraction continue.
|
|
|
|
Expression de x
en utilisant la multiplication par le conjugué.
|
|
|
|
Quel est l'entier
le plus grand inférieur à x1?
|
E
|
|
|
Valeur de x1
en fraction:
|
|
|
|
Remplacement de x1
par sa valeur:
|
|
|
|
|
|
|
||
Entier le plus
grand:
|
E
|
|
|
Nouveau nombre de
la fraction continue:
|
|
|
|
Remplacement de x2
par sa valeur:
|
|
|
|
|
|
|
||
Entier le plus
grand:
|
E
|
|
|
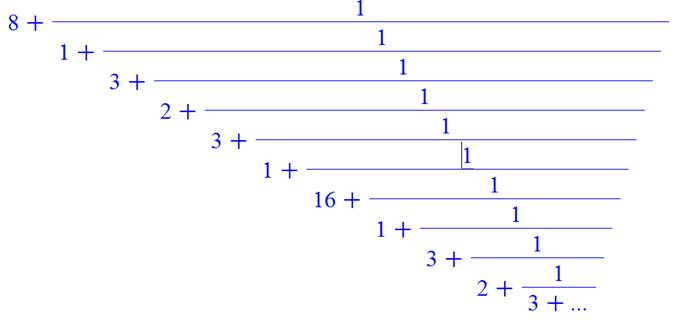
Etc.
La fraction
continue s'écrit:
|
|
|
|
Cette fraction,
en s'arrêtant à 2 devient
|
|
|
|
Si vous voulez
continuer:
|
|||
Voir DicoNombre
77
|
|
||||
Le nombre d'or
vaut
|
|
= (1 +
|
||
Solution de l'équation
|
x² – x – 1
|
= 0
|
||
On peut l'écrire
|
x²
|
= x + 1
|
||
Ou encore, en
divisant par x
|
x
|
= 1 + 1/x
|
||
Soit la fraction
continue
|
|
= 1 + 1/(1 + 1/(1 + 1/(1 + …
|
||
En abrégé
|
|
= [1, 1, 1, 1…]
|
||
|
|
||||
Soit l'équation
|
x²
– 5x – 1
|
= 0
|
||
On peut l'écrire
|
x²
|
= 5x + 1
|
||
Ou encore
|
x
|
= 5 + 1/x
|
||
Soit la fraction
continue
|
|
= 5 + 1/(5 + 1/(5 + 1/(
…
|
||
En fait les deux
solutions sont:
|
5/2
+ 1/2 .
|
5/2
- 1/2 .
|
||
Valeur numérique
|
5,192582404
|
-0,192582404
|
||
Fractions
continues
|
[5,
5, 5, 5, 5, 5, 5, …]
|
[-1,
1, 4, 5, 5, 5, 5, 5, …]
|
||
|
|
|
Les racines réelles
d'une équation du 2e degré à coefficients entiers s'expriment sous
la forme d'une fraction continue périodique.
Lagrange (1736-1813) |
|
|
|
|||
Le nombre d'or
vaut
|
|
= (1 +
|
|
On s'intéresse
aux équations :
|
|
x² – nx – 1 = 0
|
|
Dont les racines
réelles sont:
|
S(n)
|
= n + 1/(n +
1/(n + 1/(n + …
|
|
Ou, en fraction continue
|
|
= [n;
n, n, n, …]
|
|
C'est aussi
|
|
=
n + 1 / S(n)
|
|
|
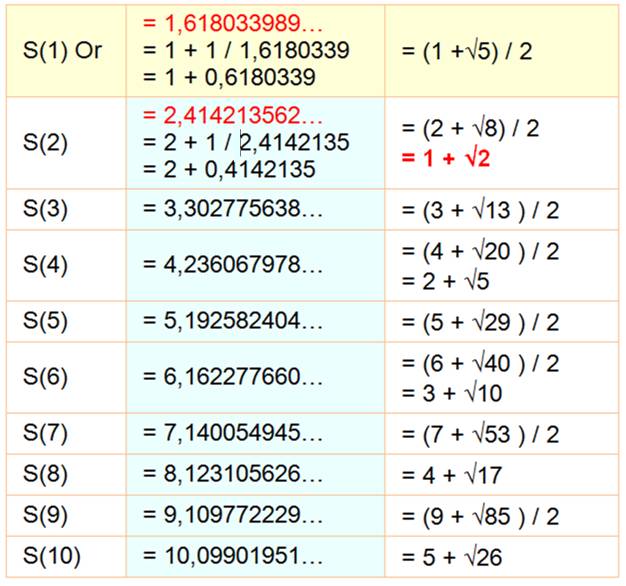
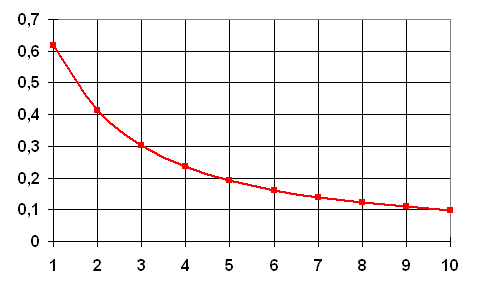
Définition Un
nombre d'argent Sn
d'ordre n est un nombre égal à l'ordre augmenté de son propre
inverse: Sn
= n + 1/Sn
Nombres d'argent jusqu'à 10 (Parfois:
nombre d'argent pour S(2) et nombres
métalliques pour la famille. S(3) sera le nombre de bronze, S(4), le
cuivre, etc.) |
|||
Voir Autre nombre d'argent
(équation du 3e degré) / Racine de deux
/ Liste
de nombres irrationnels
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
|
![]()