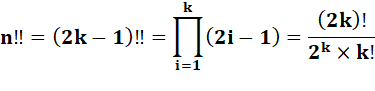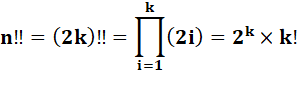NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/09/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER - Combinatoire
Débutants Dénombrement	FACTORIELLES			Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Introduction	Super-factorielle et autres
		Primorielle	Hyperfactorielle
		Sommaire de cette page >>> Factorielle plus un >>> Factorielle k-tuple >>> Factorielles doubles >>> Multifactiorielle >>> Hyperfactorielle >>> Factorielles géantes

FACTORIELLES diverses

Quelques autres formes de factorielles, dérivées des factorielles classiques.

FACTORIELLE 1
Premiers 3! – 1 = 5 4! – 1 = 23 6! – 1 = 719 7! – 1 = 5 039 Liste: 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, 379, 469, 546, 974, 1963, 3507, 3610, 6917, 21480, 34790, 94550, 103040, 147855, 208003, …	1 ! + 1 = 2 2 ! + 1 = 3 3 ! + 1 = 7 11 ! + 1 = 39 916 801
Carrés 1! – 1 = 0² 2! – 1 = 1² Exploration avec 2 et 3 1! – 2 = i² 2! – 2 = 0² 3! – 2 = 2² 2! – 3 = i²	4! + 1 = 25 = 5² 5! + 1 = 121 = 11² 7! + 1 = 5 041 = 71² Les trois seuls cas (problème de Brocard). Avec coquetterie en 71 pour le troisième. 2! + 2 = 2² 1! + 3 = 2² 3! + 3 = 3²
n! + 1 = premier: existence en nombre infini ? n! + 1 = carré: existence en nombre infini ?

Suite en Premiers factoriels / Premiers multifactoriels / Factorielle – 1

Voir Premier primoriels / Nombres complexes (i et i²) / Factorielles moins un

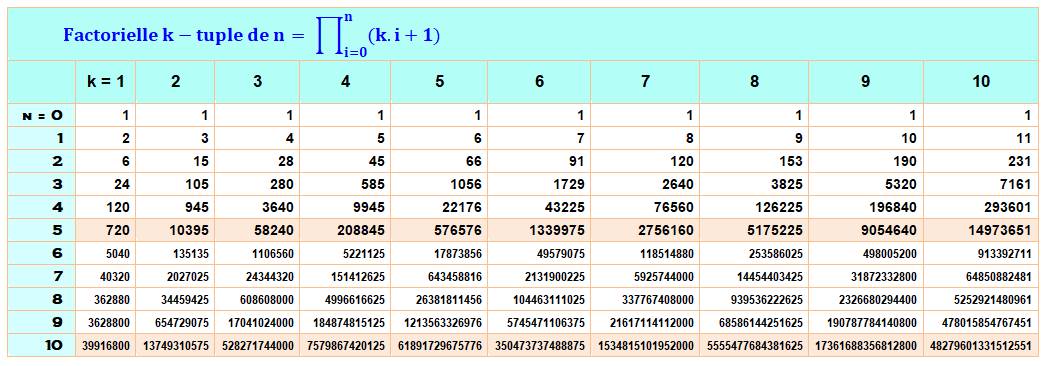
Factorielle étendue dite k-tuple

Exemple: factorielle sextuple de 3 = 1729

Factorielles doubles

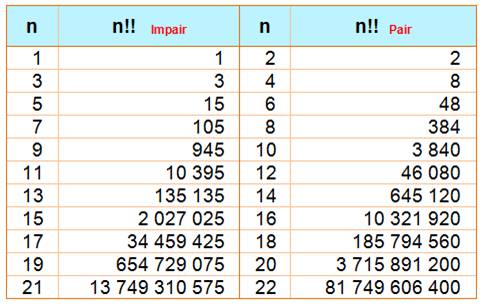
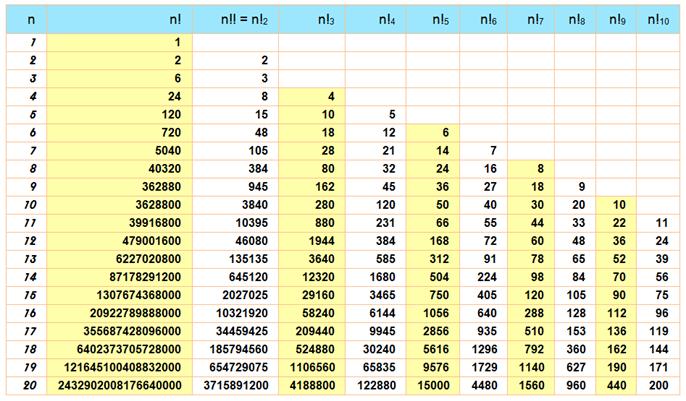
Le produit des nombres impairs successifs correspond à la factorielle "2-tuple" vue ci-dessus, dite factorielle double – Anglais: double factorial. Attention à la valeur de n le nombre impair (tableau ci-dessous) ou le n de 2n + 1 caractérisant un nombre impair (tableau ci-dessus). Le produit des nombres pairs successifs ne porte pas de nom, mais est aussi parfois appelé factorielle double. 9!! = 945 Ne pas confondre avec la factorielle de factorielle: (3!)! = (6)! = 720. Voir Calcul des factorielles en 1/2 / Nombres d'Euler de 2^e espèce Définition de la factorielle double selon que n est impair ou pair Soit un nombre impair n = 2k – 1: Exemple: Soit un nombre pair n = 2k: Exemple: Le logiciel Mapple calcule cette fonction directement avec doublefactorial. Ex: 42849873690624000

Voir Identité / Quart de finale et factorielle impaire / Puzzle utilisant les factorielles doubles

MULTI-FACTORIELLE

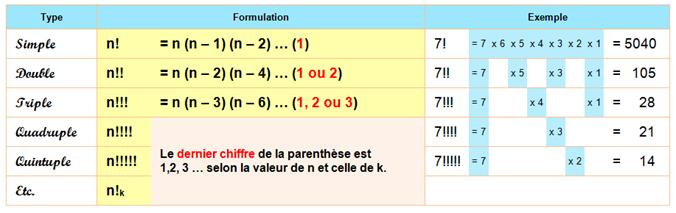
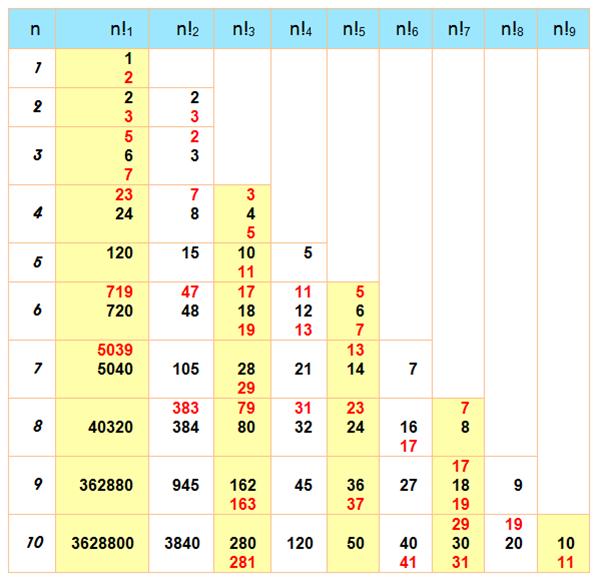
Formulation La notion de factorielle simple ou double peut être généralisée aux factorielles triples, quadruples … Tables des multifactorielles Tables des multifactorielles premières Il s'agit des multifactorielles premières moins un: notée en rouge en haut du nombre multifactoriel (noir); et des multifactorielles premières plus un: notée en rouge en bas du nombre multifactoriel. Exemples: 4! = 24 et 4! – 1 = 23 nombre premier. 6!! = 48 est double-factoriel premier par les deux côtés, en plus (49) et en moins(47), nombres qui sont tous deux premiers (jumeaux)

Voir Nombres factoriels premiers

HYPERFACTORIELLES

Hyper-puissance de factorielles ou hyperfactorielles Factorielle dont les termes sont les nombres habituels (1,2, 3 …), mais porté à la puissance égale à la valeur du terme (1^1, 2^2, 3^3 …) 3!H = 1^1 x 2^2 x 3^3 = 1 x 4 x 27 = 108 Hyper-triangulaires Même chose en remplaçant le produit par la somme HT = 1^1 + 2^2 + 3^3 = 1 + 4 + 27 = 32 Voir table >>> Hyper-somme de triangulaires Il s'agit de la somme multi-cumulée des triangulaires classiques >>>

Développements pour ces trois types en HYPERFACTORIELLES

Factorielles géantes ...

Produit-factorielle (parfois nommées superfactorielle) n$ = produit des factorielles de 1 à n 2$ = 1! x 2! = 1 x 2 = 2 3$ = 1! x 2! x 3! = 2 x 3! = 2 x 6 = 12 4$ = 1! x 2! x 3! x 4! = 12 x 24 = 288 5$ = 1! x 2! x 3! x 4! x 5! = 288 x 120 = 34 560 Notion introduite par Sloane and Plouffe Voir Divisibilité des produits de différences Superfactorielles Superfactorielle de n = n^! = factorielle de n à la puissance n! et cela n! fois. 2^! = 2^2^2 = 2^4 = 16 3^! = 6^6^6^6^6^6^6 = 6^6^6^6^6^46656 = 6^6^6^6^2659… avec le dernier exposant égal à 0,26 10^36306; 6 puissance ce nombre dépasse la capacité de calcul des logiciels spécialisés. n^! 2 = superfactorielle n à la puissance superfactorielle de n et cela superfactorielle n fois. Nombre au-delà de l'imagination! L'indice 2 peut passer à 3, 4 … Voici ce qu'en dit un l'auteur de cette notation(Sanchez): Three standard arithmetic symbols, 9^! 9, is all we need to define a finite number so large that the standard writing of its precise sequence of digits would surely require a volume of paper much more greater than the volume of the visible universe. (Pour écrire ce nombre, le volume de papier dépasserait largement la taille de l'Univers). Notion introduite par C.A.Pickover et Antonio L. Sánchez

Suite	Nombres permutés Factorielle et dénombrement Factorielle: nième différence d'une puissance n Somme alternée de factorielles tronquées = 1/2 Voir haut de page
Voir	Compter Débutant et dénombrement Divisibilité de la somme des entiers par des factorielles Factorielle: nième différence d'une puissance n Factorielles divisées Factorielles et grands nombres Factorielles et leurs diviseurs Factorielles impaires Formule de Stirling Nombres de Stirling Problème de Brocard (n! + 1 = k²) Programmer la fonction factorielle Théorème de Wilson
Sites	OEIS A000165 – Double factorial of even numbers: (2n)!! = 2^n*n! OEIS A002982 – Numbers n such that n! - 1 is prime OEIS A002981 – Numbers k such that k! + 1 is prime Factorial Prime – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/SixFact1.htm