NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/11/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	CONSTRUCTIONS			Glossaire Géométrie
INDEX Géométrie	Constructible	Bissection	Trisection
		Bissection du triangle
		Sommaire de cette page >>> Bissection du segment – Médiatrice >>> Bissection de l'angle – Bissectrice >>> Bissection de l'angle – Avec allumettes >>> Bissection du carré >>> Carré et triangle

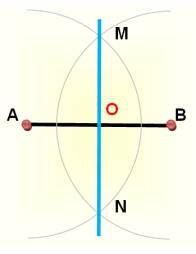
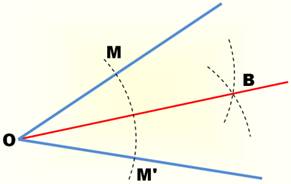
BISSECTION

Comment couper en deux parties égales un segment, un angle ?

Bissection du segment – Médiatrice
La construction de la médiatrice partage, par définition, le segment en deux segments égaux. Cercle de rayon R en A, Cercle de rayon R en B, Intersection en M et N, MN est la médiatrice, AO = OB. Et aussi: MO = ON.

Bissection de l'angle – Bissectrice
La construction de la bissectrice partage, par définition, l'angle en deux angles égaux. Cercle de rayon R en 0, Intersection en M et M', Cercle de rayon R' en M, Cercle de rayon R' en N, AB est la bissectrice.

Voir Bissectrice dans le triangle

Bissection de l'angle – Avec allumettes
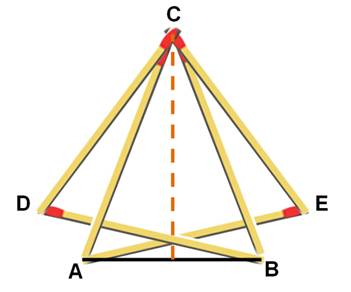
Bissection du segment AB avec des allumettes. Chaque segment (hors AB) est une allumette, soit: 7 allumettes. Théorème T.R. Dawson, célèbre pour ses problèmes d'échecs, découvrit que: Les constructions à la règle et au compas sont possibles si, et seulement si, elles le sont avec des allumettes identiques.

Bissection du carré en carrés
Comment découper un carré pour en obtenir deux égaux à la moitié de l'original? Voici deux solutions classiques. La seconde rappelle une démonstration simpliste du théorème de Pythagore. La première est optimale; elle ne comporte que quatre pièces.

Carré et triangle		haut
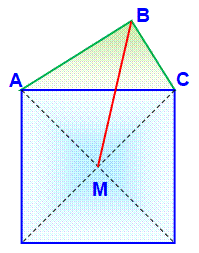
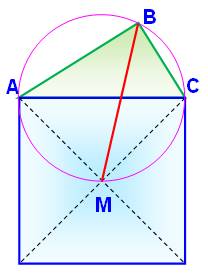
Problème Un triangle rectangle ABC. Un carré construit sur l'hypoténuse AC. Son centre M. Montrer que BM est la bissectrice de l'angle ABC. Solution Dessiner le centre circonscrit au triangle rectangle. Son hypoténuse AC est un diamètre. L'angle en M, où se rencontrent les diagonales du carré, est droit. Le point M est sur le cercle ABC. Les arcs AM et MC sont égaux et les angles qui les sous-tendent sont égaux. 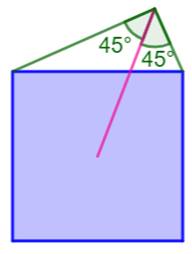BM est la bissectrice de l'angle ABC et chaque angle vaut 45°. Construction Comment construire la bissectrice d'un angle droit ? Construire un triangle rectangle, avec une hypoténuse quelconque et dessiner le carré sur cette hypoténuse. Trouver le centre du carré à l'aide des deux diagonales. Joindre ce point au sommet de l'angle droit (segment rose). C'est la bissectrice de l'angle droit.
Théorème La droite qui passe par le centre du carré et par le sommet à angle droit d'un triangle rectangle en "chapeau" sur le carré est la bissectrice de l'angle droit.

Voir Brève 736 / Méthodes de constructions

Suite	Bissectrice Bissection du triangle Trisection
Voir	Allumettes Construction de racine de 2 Centre du cercle Pentagone ou étoile à cinq branches
Autres	Cycloïde Géométrie – Index Heptagone Illusions d'optique Jeux – Index Médiatrice Neusis (construction-) Pliages et découpages Polyèdres Polygones Quadrature du cercle Triangles
DicoNombre	Nombre 2
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Bissecti.htm