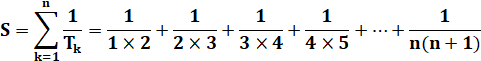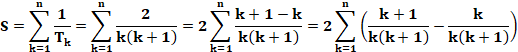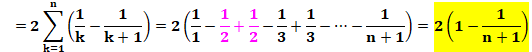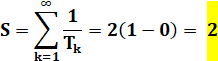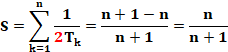|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES D'INVERSES Développements Voir
Liste des formules avec les inverses |
|
|
|
|
Particulier
Général La somme des inverses de tous les nombres tend
lentement vers l'infini. C'est la série
harmonique: 1/1 + 1/2 + 1/3 + … Aucune formule générique pour donner cette somme pour le rang n. Quelques
sommes
Pour
des nombres successifs
|
|
|
|
|
|
Un nombre
triangulaire est de la forme: Tn = n (n + 1) / 2, produit de
deux nombres successifs divisé par 2. Il représente la somme de tous les
nombres entiers de 1 à n. Somme finie des
inverses
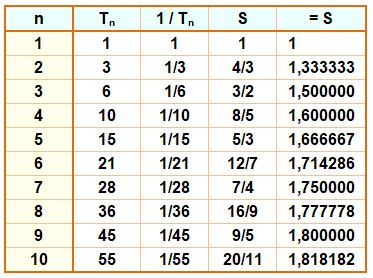
Exemple sur les
premières valeurs
Calcul de la somme
finie des inverses
Somme infinie des
inverses
Remarque
Exemple
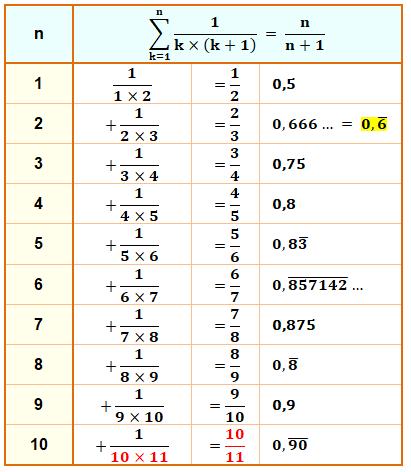
pour n = 100, la somme vaut simplement 100 / 101 (= 0,9900 9900 …) Ce qui permet de construire ce tableau sympathique:
La
somme de tous les inverses de produits de deux consécutifs jusqu'à
n est égal à n / (n+1). Méthode de calcul sur
un exemple (pour exercice de vérification)
|
|
Voir Nombres
triangulaires – Somme / Brève
513 / Brève
524 / Nombre
0,8
|
|
|
|
Produit
des inverses Le produit des inverses est égal à l'inverse de la
factorielle: 1/1 x 1/2 x 1/3 x
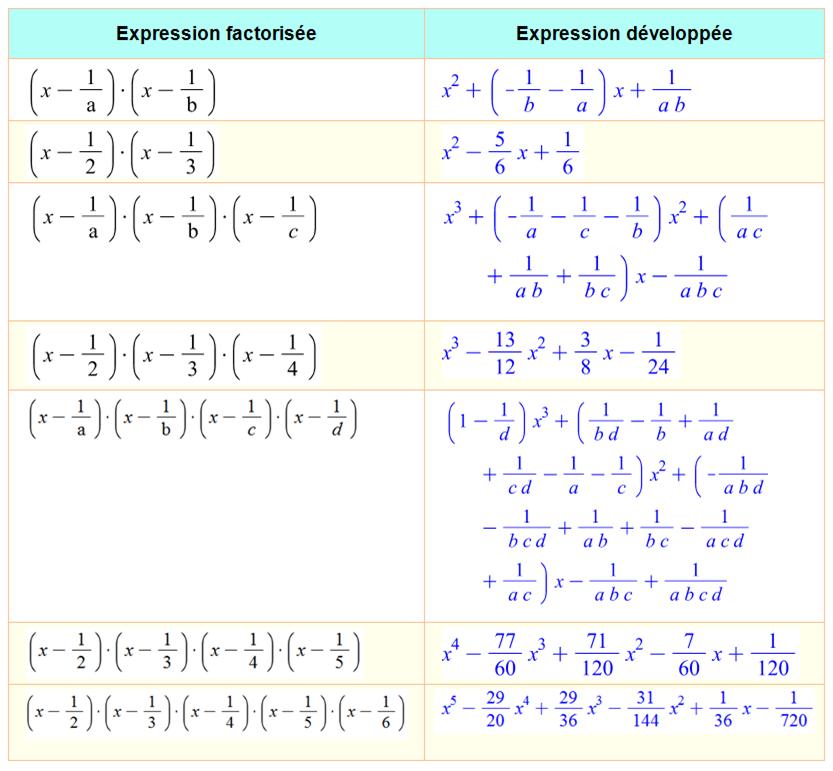
… x 1/n = 1 / n! Opposés
des inverses
Etc. Il s'agit du produit de fractions dont le
numérateur est égal au dénominateur moins une unité, comme: 1 – 1/4 = 3/4. Exemple de produit 2/3 x 6/7 x 7/8 =
(2x6x7)/(3x7x8) = ½. Avec
des nombres L'expression se simplifie grandement lorsque les
nombres se suivent. Seules les deux extrémités résistent, comme dans: 3/4 x 4/5 x 5/6 = 3/6. Simplification maximale, en commençant par 1/2: Exemple: Numérateur et dénominateur se simplifient. Général
|
|
|
|
|
|
Produit
des inverses des carrés Le produit des inverses des carrés est égal à
l'inverse de la factorielle au carré: 1/1² x 1/2² x
1/3² x … x 1/n² = 1
/ (n!)² Opposés
des inverses au carré
Etc. Il s'agit du produit de fractions dont le
numérateur est égal au dénominateur moins une unité. Avec
des nombres En remplaçant les lettres par les nombres
successifs: (1 – 1/2²) (1 –
1/3²) (1 – 1/4²) … (1 – 1/n²) = (n + 2) / (2n + 2) Pour n =
2: 4/6 = 0,666… & (1-1/4)(1-1/9) =3/4 x 8/9 = 2/3 = 0,666… Pour n =
10: 12/22 = 0,54545454… Pour n = 100: 102/202 = 0,5049504950… Pour n très grand, la valeur tend vers 1/2. Pour
des nombres successifs
Application:
(1-1/2²) (1-1/3²) (1-1/4²) = (9-4) / (9-1) = 5/8 Vérification: (1-1/2²) (1-1/3²) (1-1/4²) = 3/4 x 8/9 x 15/16 = 5/8 |
|
Voir Somme de carrés
/ Somme des inverses des carrés
|
|
|
|
Voici l'art de créer des fractions dont numérateur
et dénominateur ne différent que d'une unité; le dénominateur étant un carré.
Suite des fractions produites par cette
expression: {3/4, 8/9, 15/16,
24/25, 35/36, 48/49 …} D= carré
et N = D-1. |
|
|
|
|
|
Voici l'art de créer des fractions dont les
dénominateurs sont la suite de tous les nombres impairs:
Le numérateur, produit de deux nombre consécutifs,
est pair. La fraction se simplifie toujours par 2. Le dénominateur vaut 2n +
1, un nombre impair. Valeurs pour n de 1 à
20 n Terme Somme Valeur 1 1/3 1/3 0, 333333333 2 4/15 3/5 0, 6 3 9/35 6/7 0, 857142857 4 16/63 10/9 1,
111111111 5 25/99 15/11 1,
363636364 6 36/143 21/13 1,
615384615 7 49/195 28/15 1,
866666667 8 64/255 36/17 2,
117647059 9 81/323 45/19 2,
368421053 10 100/399 55/21 2, 619047619 11 121/483 66/23 2, 869565217 12 144/575 78/25 3, 120000000 13 169/675 91/27 3, 370370370 14 196/783 105/29 3, 620689655 15 225/899 120/31 3, 870967742 16 256/1023 136/33 4,
121212121 17 289/1155 153/35 4,
371428571 18 324/1295 171/37 4,
621621622 19 361/1443 190/39 4,
871794872 20 400/1599 210/41 5,
121951220 |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentInv.htm
|
![]()