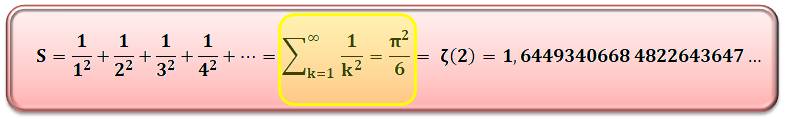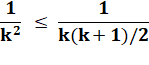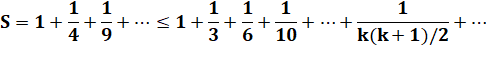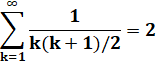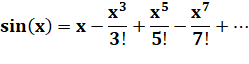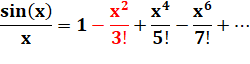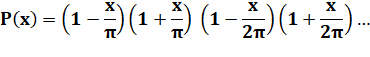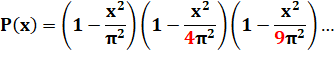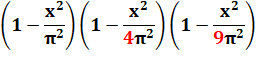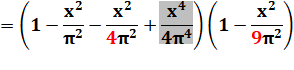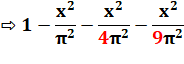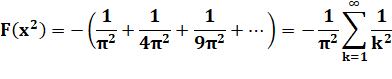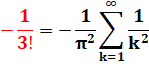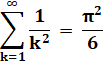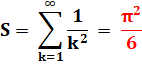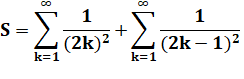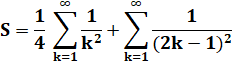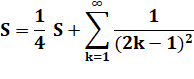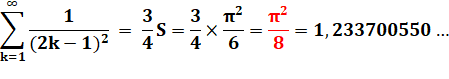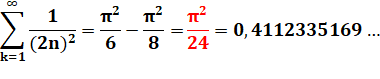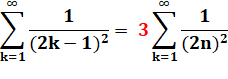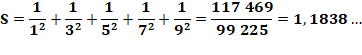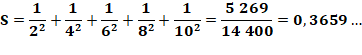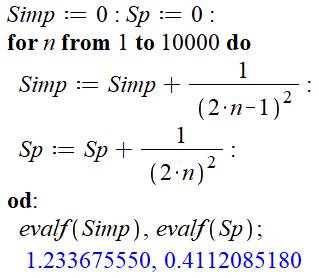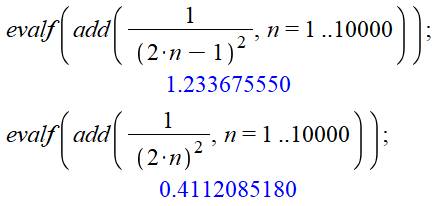|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES des INVERSES des CARRÉS avec nombres consécutifs dit: problème de Bâle ou problème de Mengoli
Le problème de la convergence de
cette série est souvent traité sur Internet. Il existe plusieurs
démonstrations. Aucune n'est simple. Sur cette page, la première
démonstration d'Euler qui a le mérite de rester à un niveau raisonnable. Elle
donne la solution même au prix d'une petite impasse formelle reconnue par
Euler lui-même. |
Anglais: Sum of
reciprocal squares / Basel problem /
Summing the infinite series of reciprocals of integers squared.
|
Au XIVe siècle, Oresme
traite de la divergence de la série
harmonique somme des inverses des entiers. 1644: Pietro Mengoli (1626-1686) pose la question: que vaut S? dans
son livre: quadraturae arithmetica qui traite de la sommation des séries. 1664: John Wallis tente le calcul. 1691: Jacob Bernoulli
(1654-1705) prouve que S < 2. La
famille Bernoulli est sur le coup, et aussi Leibniz, Stirling, de Moivre. 1731: Leonard Euler
(1707-1763) trouve 6 décimales. Pas faciles à trouver, car la série converge très lentement. 1733: il calcule 20 décimales. 1735: il atteint une infinité de décimale en démontrant que S = Pi² /
6 dans son article: de summis serierum reciprocarum. 1741: il propose une démonstration rigoureuse. 1748: il publie: Introductio in analysin infinitorum (Introduction à
l’analyse infinitésimale) qui restera une référence pendant près de cent ans. 1859: Bernhard Riemann
(1826-1866) définit la fonction zêta
et énonce son hypothèse
concernant les nombres premiers. Pourquoi problème de Bâle? Parce qu'Euler passa son enfance à Bâle et
y suivit ses cours d'université. |
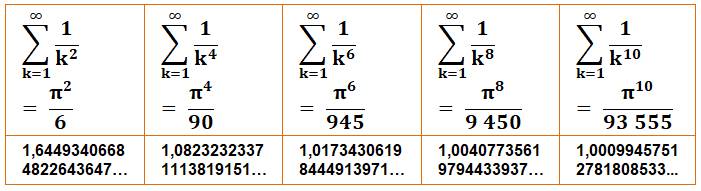
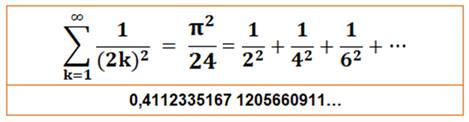
|
Après les inverses des
carrés, Euler a réussi à donner les formules pour les puissances paires.
Déduire d'autres formules comme celle de la somme des inverses des impairs au
carré est alors assez simple. En 1978, Roger Apéry a
prouvé que la somme pour les puissances impaires est irrationnelle. La manière d'obtenir la somme
est toujours inconnue à ce jour. |
Voir Tableau
des valeurs
![]()
|
|
||
|
Il pose l'inégalité: |
|
|
|
Il passe aux inverses: |
|
|
|
Application pour majorer la somme S. |
|
|
|
On savait à l'époque que: |
|
|
|
Il en déduit que: |
|
|
|
Il n'a pas réussi à aller plus loin et a écrit:
si quelqu'un trouve et nous communique ce qui jusqu'à présent a échappé à nos
efforts, grande sera notre gratitude. |
||
Source: Leonhard
Euler and the Basel Problem – Amber Emmel
|
|
||
|
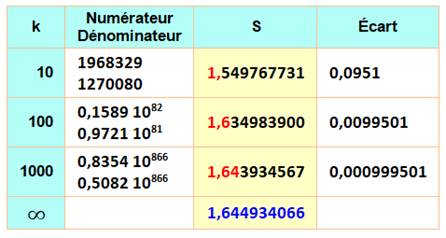
On
imagine la patience d'Euler pour calculer ses 20 décimales de S en observant
la lenteur de la convergence. Avec 1000
termes, on n'obtient que 2 décimales et la fraction irréductible comporte
déjà plus de 800 chiffres. Euler
utilise une formule faisant intervenir le développement connu de log(2) et
une fonction qu'il a mise au point: le dilogarithme. |
Tableau montrant la lente
convergence
La fonction dilogarithme utilisée
par Euler
|
|
|
|
||
|
Développement
de la fonction sinus x |
|
|
|
Exemple de convergence avec ces trois termes. Convergence d'autant plus rapide que x est petit. |
sin (1/10) Valeur= 0,09983341664682815 Calcul = 0,09983341664682539 sin (1/2) Valeur= 0,47942553860 Calcul = 0,47942553323 |
|
|
Division par x |
|
|
|
Racines pour |
|
|
|
Polynôme ayant ces mêmes racines. |
|
|
|
Identité remarquable pour
chaque paire: |
|
|
|
Exemple du développement du produit avec trois termes en laissant tomber les
termes de degré supérieur à 2. |
|
|
|
Développement du produit en ne conservant que le
terme en x²: |
|
|
|
Comparaison au terme en x² du sinus: |
|
|
|
Finalement: |
|
|
|
On
reproche à cette démonstration d'extrapoler les propriétés des polynômes
finis aux polynômes infinis. Euler à néanmoins conforté ce résultat avec son
calcul numérique sur 20 décimales. Six ans plus tard, il propose une
démonstration sans faille. Voir les sites en références pour
d'autres démonstrations. |
|
|
|||
|
Somme
pour tous les nombres: |
|
||
|
Somme
explicite avec les pairs et les impairs: |
|
||
|
En
sortant le facteur 2: |
|
||
|
Le
premier terme est connu: |
|
||
|
Somme
pour impairs |
|
||
|
Somme
pour pairs |
|
||
|
Notez le
rapport 3 |
La somme des inverses des carrés des nombres impairs
est égale à trois fois celle pour les nombres
pairs. |
||
|
Exemples
avec n = 5 |
|
|
Calcul
avec Maple L’instruction
evalf donne la valeur décimale de
la fraction calculée. |
|
|
Autre
forme plus rapide avec l’instruction addition
de x à y. |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomInvCa.htm
|
![]()