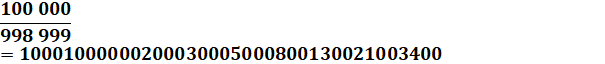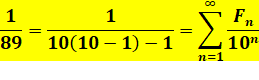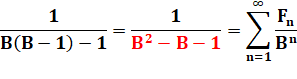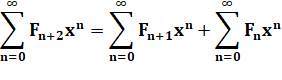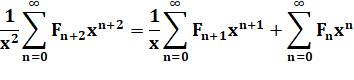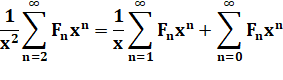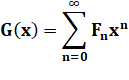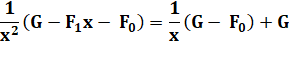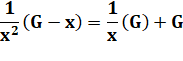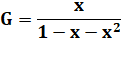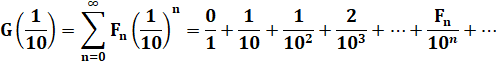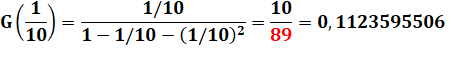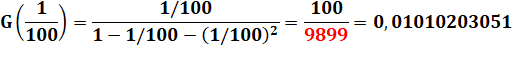|
||||||||||||||||||||||||||||||||||
![]()
|
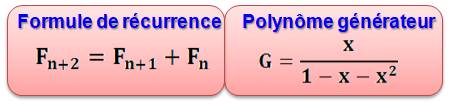
FIBONACCI – 1/89 Polynômes générateurs La
fraction 1/89 contient en son sein tous les nombres
de Fibonacci. Certes, ils sont enfouis parce que les plus grands se
bousculent entre eux par effet de retenues sur les sommes. Quelle est
la raison de cette propriété? Une explication passe par le polynôme
générateur de la formule
de récurrence définissant les nombres de Fibonacci.
|
|
|
||
|
Suite des nombres de Fibonacci Les
douze premiers des nombres de Fibonacci. |
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 … Notez
que F11
= 89 |
|
|
Concaténation de ces nombres Avec
cette seule suite, l'inverse fait apparaitre non seulement le nombre 89
(déjà) et également, le début de la concaténation d'origine. |
Fc = 0,1123581321345589144 … 1/Fc = 8,9001123550399… |
|
|
Une simple division Avec
les premiers nombres de Fibonacci, la division montre déjà un résultat
intéressant: le nombre 89. |
Ff = 1 / 0,0112358 = 89,0012… |
|
|
|
||
|
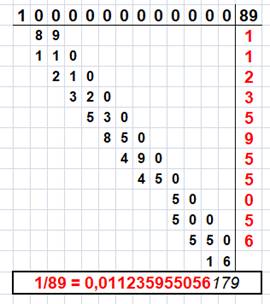
Nombre 89 Le
développement décimal de la fraction 1/89 fait apparaitre les premières
valeurs des nombres de Fibonacci: 1, 1, 2, 3, 5 (Division longue ci-contre).
Notez les restes: on y retrouve
les deux nombres à sommer: (1+1), (2+1), (3+2), … Période L
est la longueur de la période
de la fraction. Avec 1/89, le même bloc de L = 44 chiffres est répété sans
fin. Notez que
le diviseur 89
est lui-même un nombre de Fibonacci (coïncidence). |
Division 1
Suite de la Somme
(Excel) |
|
|
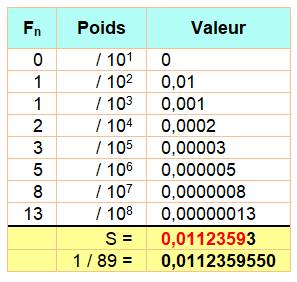
La
suite du développement décimal cache-elle aussi les nombres de Fibonacci
suivants? Oui,
car la somme des nombres de Fibonacci pondérée par les inverses des
puissances de 10 reconstruit progressivement la valeur de la fraction 1/89 en
tenant compte des retenues (Tableau). |
Somme pondérée des nombres de Fibonacci
|
|
Voir Fractions qui engendrent des
suites de nombres
|
|
|||
|
Expérience à deux chiffres Concaténation
des nombres de Fibonacci avec deux chiffres. Il semblerait que 9 899 soit un
bon numéro … |
Ff = 0,101020305081321345589 … 1/Ff = 9,89900000000000000014… |
||
|
Nombre 9 899 Avec
9 899, la fraction laisse de la place aux sommes intermédiaires pour
s'exprimer. Effectivement,
les Fibonacci à deux chiffres jusqu'à 55 se retrouvent dans le développement
de la fraction. Avec
998 999, tous les nombres de Fibonacci à trois chiffres sont présents sauf le
dernier, victime d'une retenue avec l'addition du suivant (988 au lieu de
987). On vérifie bien que: 233 + 377 = 610. Ajoutez
un 9 de part et d'autres et vous aurez encore plus de Fibonacci apparents (ci-dessous). |
|
||
|
Avec cette fraction on arrive jusqu'à 4 181 et le
suivant 6 765 est incrémenté de 1. |
|||
|
Nombre 109 On
retrouve de la même manière la suite de Fibonacci dans la fraction 1/109,
mais à l'envers, à la fin de la période de la fraction. |
|
||
|
Il
est aussi possible d'atteindre la fraction 1 /109 à l'endroit avec les
nombres de Fibonacci. La séquence est la même que pour 1/89, mais alternée: |
0 / 101 + 1 / 102
– 1 / 103 + 2 / 104 – 3 / 105
+ 5 / 106 – … =
0,009174 … = 1/109 |
||
|
Rien
n'explique de manière évidente le fait que cette fraction soit liée aux
nombres de Fibonacci. Certains
tentent des explications via le triangle
de Pascal et l'effet du nombre 11 (= 100 – 89). L'explication
passe, en fait, par le calcul de la fonction génératrice de la formule de
récurrence. |
Bilan en base 10
Et en base quelconque
En base 11, la fraction serait 1/109. En binaire c'est 1/1. |
Voir Somme
rationnelle avec les nombres de Fibonacci ou de Lucas
|
|
|||
|
Fonction de récurrence Définition des nombres de Fibonacci |
|
||
|
En multipliant par xn Avec l'idée de le remplacer par (1/10)n en fin de calcul |
|
||
|
Sommes de 0 à l'infini Possible, car sommation termes à termes |
|
||
|
Indices et puissances homogènes en divisant par 1/x² et 1/x |
|
||
|
Mêmes sommes, mais en modifiant les bornes de sommation |
|
||
|
Introduction d'une fonction génératrice Celle-ci, parait évidente |
|
||
|
Remplacement en tenant compte des bornes de sommation |
|
||
|
Simplification avec F1 = 1 et F0 = 0 (cf. définition des
nombres de Fibonacci) |
|
||
|
Équation En multipliant par x² |
|
||
|
Expression de G(x) |
|
||
|
Expression de G(1/10) Selon la définition et selon la forme trouvée |
|
||
|
Expression de G(1/100) |
|
||
|
Nombres inverses de Fibonacci Tous générés en flanquant l'ancien par un 9 de chaque côté |
Fi (n) = 102n – 10n – 1 = 10n (10n
– 1) – 1 ð 89, 9899, 998999, …
99n-18999n |
||
Voir Polynômes générateurs des
nombres k-bonacci
Merci à Franck Douay pour son questionnement
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()