|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Cycle de Syracuse ou de Collatz Généralisé avec des nombres
premiers
|
Anglais Collatz-2 map
|
|
||||||
|
Exemples |
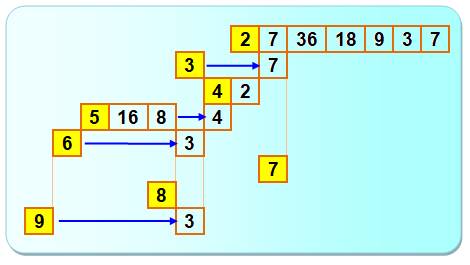
Selon le procédé expliqué en image ci-dessus: Le nombre
3 est premier,
il est multiplié par le premier précédent qui est: 2. L'image du nombre 3 est
le produit de ces deux nombres premiers augmenté de 1, donc 3 x 2 + 1 = 7. Le nombre
8 est composé
et son plus petit facteur (le seul en l'occurrence) est 2. L'image du nombre
8 est 8 / 2 = 4. |
|||||
|
Cas du nombre 2 |
Le nombre
2 est un nombre premier sans prédécesseur (le nombre
1 n'est pas considéré comme premier). Exception ici, on utilisera la
nombre 1 comme prédécesseur. L'image du nombre 2 est donc 2 x 1 + 1 = 3. |
|||||
|
Premier nombres Nombres premiers |
2,
3 3,
7 4, 2 5,
16 6, 3 7,
36 8, 4 9, 3 10, 5 11,
78 12, 6 13,
144 14, 7 15, 5 16, 8 17,
222 18, 9 19,
324 |
20, 10 21, 7 22, 11 23,
438 24, 12 25, 5 26, 13 27, 9 28, 14 29,
668 30, 15 31,
900 32, 16 33, 11 34, 17 35, 7 36, 18 37,
1148 38, 19 39, 13 |
40, 20 41,
1518 42, 21 43,
1764 44, 22 45, 15 46, 23 47,
2022 48, 24 49, 7 50, 25 51, 17 52, 26 53,
2492 54, 27 55, 11 56, 28 57, 19 58, 29 59,
3128 |
60, 30 61,
3600 62, 31 63, 21 64, 32 65, 13 66, 33 67,
4088 68, 34 69, 23 70, 35 71,
4758 72, 36 73,
5184 74, 37 75, 25 76, 38 77, 11 78, 39 79,
5768 |
80, 40 81, 27 82, 41 83,
6558 84, 42 85, 17 86, 43 87, 29 88, 44 89,
7388 90, 45 91, 13 92, 46 93, 31 94, 47 95, 19 96, 48 97,
8634 98, 49 99, 33 100, 50 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Exemple avec 3 Avec le nombre 3, création d'un cycle qui boucle
sur le nombre 3 lui-même. Notation: nombre, quantité de
cycles, suite |
|
||||||||||||||||||||||||||||||||||||||
|
Exemple avec 11 Avec le nombre 3, création d'un cycle de 11
itérations qui bouclent ensuite sur le 36. Ou sur le 3, le cycle vu ci-dessus. On dit que 11 termine son cycle sur le 3. Notation: nombre, quantité de
cycles, suite |
|
||||||||||||||||||||||||||||||||||||||
|
Trajectoires pour les premiers
nombres |
2, 6, [2, 7, 36, 18, 9, 3, 7] 3, 5, [3, 7, 36, 18, 9, 3] 4, 7, [4, 2, 7, 36, 18, 9, 3, 7] 5, 10, [5, 16, 8, 4, 2, 7, 36, 18,
9, 3, 7] 6, 6, [6, 3, 7, 36, 18, 9, 3] 7, 5, [7, 36, 18, 9, 3, 7] 8, 8, [8, 4, 2, 7, 36, 18, 9, 3, 7] 9, 5, [9, 3, 7, 36, 18, 9] Relations entre les trajectoires des nombre 2 à 9
Voir Brève
794 10, 11, [10, 5, 16, 8, 4, 2, 7, 36,
18, 9, 3, 7] 11, 11, [11, 78, 39, 13, 144, 72, 36,
18, 9, 3, 7, 36] 12, 7, [12, 6, 3, 7, 36, 18, 9, 3] 13, 8, [13, 144, 72, 36, 18, 9, 3,
7, 36] 14, 6, [14, 7, 36, 18, 9, 3, 7] 15, 11, [15, 5, 16, 8, 4, 2, 7, 36,
18, 9, 3, 7] 16, 9, [16, 8, 4, 2, 7, 36, 18, 9,
3, 7] 17, 28, [17, 222, 111, 37, 1148, 574,
287, 41, 1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324, 162,
81, 27, 9, 3, 7, 36, 18, 9] 18, 5, [18, 9, 3, 7, 36, 18] 19, 10, [19, 324, 162, 81, 27, 9, 3,
7, 36, 18, 9] 20, 12, [20, 10, 5, 16, 8, 4, 2, 7,
36, 18, 9, 3, 7] 21, 6, [21, 7, 36, 18, 9, 3, 7] 22, 12, [22, 11, 78, 39, 13, 144,
72, 36, 18, 9, 3, 7, 36] 23, 17, [23, 438, 219, 73, 5184,
2592, 1296, 648, 324, 162, 81, 27, 9, 3, 7, 36, 18, 9] 24, 8, [24, 12, 6, 3, 7, 36, 18, 9,
3] 25, 11, [25, 5, 16, 8, 4, 2, 7, 36,
18, 9, 3, 7] 26, 9, [26, 13, 144, 72, 36, 18, 9,
3, 7, 36] 27, 6, [27, 9, 3, 7, 36, 18, 9] 28, 7, [28, 14, 7, 36, 18, 9, 3, 7] 29, 15, [29, 668, 334, 167, 27222,
13611, 4537, 349, 121104, 60552, 30276, 15138, 7569, 2523, 841, 29] 30, 12, [30, 15, 5, 16, 8, 4, 2, 7,
36, 18, 9, 3, 7] 31, 16, [31, 900, 450, 225, 75, 25,
5, 16, 8, 4, 2, 7, 36, 18, 9, 3, 7] 32, 10, [32, 16, 8, 4, 2, 7, 36, 18,
9, 3, 7] 33, 12, [33, 11, 78, 39, 13, 144,
72, 36, 18, 9, 3, 7, 36] 34, 29, [34, 17, 222, 111, 37, 1148,
574, 287, 41, 1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324,
162, 81, 27, 9, 3, 7, 36, 18, 9] 35, 6, [35, 7, 36, 18, 9, 3, 7] 36, 5, [36, 18, 9, 3, 7, 36] 37, 25, [37, 1148, 574, 287, 41,
1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324, 162, 81, 27, 9,
3, 7, 36, 18, 9] 38, 11, [38, 19, 324, 162, 81, 27,
9, 3, 7, 36, 18, 9] 39, 9, [39, 13, 144, 72, 36, 18, 9,
3, 7, 36] 40, 13, [40, 20, 10, 5, 16, 8, 4, 2,
7, 36, 18, 9, 3, 7] 41, 21, [41, 1518, 759, 253, 23,
438, 219, 73, 5184, 2592, 1296, 648, 324, 162, 81, 27, 9, 3, 7, 36, 18, 9] 42, 7, [42, 21, 7, 36, 18, 9, 3, 7] 43, 11, [43, 1764, 882, 441, 147,
49, 7, 36, 18, 9, 3, 7] 44, 13, [44, 22, 11, 78, 39, 13,
144, 72, 36, 18, 9, 3, 7, 36] 45, 12, [45, 15, 5, 16, 8, 4, 2, 7,
36, 18, 9, 3, 7] 46, 18, [46, 23, 438, 219, 73, 5184,
2592, 1296, 648, 324, 162, 81, 27, 9, 3, 7, 36, 18, 9] 47, Voir ci-dessous 48, 9, [48, 24, 12, 6, 3, 7, 36, 18,
9, 3] 49, 6, [49, 7, 36, 18, 9, 3, 7] 50, 12, [50, 25, 5, 16, 8, 4, 2, 7,
36, 18, 9, 3, 7] |
||||||||||||||||||||||||||||||||||||||
|
Cas de 47 On ne sait pas si cette trajectoire a une fin |
47, 30+,
[47, 2022, 1011, 337, 111548, 55774, 27887, 353, 123198, 61599, 20533,
421357694, 210678847, 44385566460664754, 22192783230332377, 1707137171564029,
165918667661, 27529004277737692540278, 13764502138868846270139,
4588167379622948756713, 352935952278688365901, 3237944516318241889,
1577861856421, 2489648037916767181800822, 1244824018958383590900411,
414941339652794530300137, 138313779884264843433379, 19759111412037834776197,
534030038163184723681, 285188081660572532393784573111906997163504,
142594040830286266196892286555953498581752,
…] |
||||||||||||||||||||||||||||||||||||||
|
Trajectoire pour les premiers
nombres, AVEC: Arrêt si le nombre est déjà dans une suite
précédente |
2, 6, [2, 7, 36, 18, 9, 3, 7] 3, 1, [3, 7] Arrêt car le 7
a déjà été trouvé et on connait donc la suite 4, 1, [4, 2] 5, 3, [5, 16, 8, 4] 6, 1, [6, 3] 7, 1, [7, 36] 8, 1, [8, 4] 9, 1, [9, 3] 10, 1, [10, 5] 11, 6, [11, 78, 39, 13, 144, 72, 36] 12, 1, [12, 6] 13, 1, [13, 144] 14, 1, [14, 7] 15, 1, [15, 5] 16, 1, [16, 8] 17, 23, [17, 222, 111, 37, 1148,
574, 287, 41, 1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324,
162, 81, 27, 9] 18, 1, [18, 9] 19, 1, [19, 324] 20, 1, [20, 10] 21, 1, [21, 7] 22, 1, [22, 11] 23, 1, [23, 438] 24, 1, [24, 12] 25, 1, [25, 5] 26, 1, [26, 13] 27, 1, [27, 9] 28, 1, [28, 14] 29, 15, [29, 668, 334, 167, 27222,
13611, 4537, 349, 121104, 60552, 30276, 15138, 7569, 2523, 841, 29] 30, 1, [30, 15] 31, 5, [31, 900, 450, 225, 75, 25] 32, 1, [32, 16] 33, 1, [33, 11] 34, 1, [34, 17] 35, 1, [35, 7] 36, 1, [36, 18] 37, 1, [37, 1148] 38, 1, [38, 19] 39, 1, [39, 13] 40, 1, [40, 20] 41, 1, [41, 1518] 42, 1, [42, 21] 43, 6, [43, 1764, 882, 441, 147, 49,
7] 44, 1, [44, 22] 45, 1, [45, 15] 46, 1, [46, 23] 47, 20+,
Voir ci-dessus 48, 9, [48, 24, 12, 6, 3, 7, 36, 18,
9, 3] 49, 1, [49, 7] 50, 7, [50, 25, 5, 16, 8, 4, 2, 7] 51, 29, [51, 17, 222, 111, 37, 1148,
574, 287, 41, 1518, 759, 253, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324,
162, 81, 27, 9, 3, 7, 36, 18, 9] 52, 5, [52, 26, 13, 144, 72, 36] 53, 20+,
[53, 2492, 1246, 623, 89, 7388, 3694, 1847, 3381858, 1690929, 563643, 187881,
62627, 3921514860, 1960757430, 980378715, 326792905, 65358581, 1519967,
2310275361618, 1155137680809, … ?] 54, 2, [54, 27, 9] 55, 4, [55, 11, 78, 39, 13] 56, 3, [56, 28, 14, 7] 57, 2, [57, 19, 324] 58, 16, [58, 29, 668, 334, 167,
27222, 13611, 4537, 349, 121104, 60552, 30276, 15138, 7569, 2523, 841, 29] 59, 5, [59, 3128, 1564, 782, 391,
23] 60, 3, [60, 30, 15, 5] 61, 7, [61, 3600, 1800, 900, 450,
225, 75, 25] 62, 2, [62, 31, 900] 63, 2, [63, 21, 7] 64, 2, [64, 32, 16] 65, 1, [65, 13] 66, 2, [66, 33, 11] 67, 5, [67, 4088, 2044, 1022, 511,
73] 68, 2, [68, 34, 17] 69, 1, [69, 23] 70, 2, [70, 35, 7] 71, 4, [71, 4758, 2379, 793, 61] 72, 1, [72, 36] 73, 1, [73, 5184] 74, 1, [74, 37] 75, 1, [75, 25] 76, 2, [76, 38, 19] 77, 1, [77, 11] 78, 1, [78, 39] 79, 11, [79, 5768, 2884, 1442, 721,
103, 10404, 5202, 2601, 867, 289, 17] 80, 4, [80, 40, 20, 10, 5] 81, 1, [81, 27] 82, 1, [82, 41] 83, 13, [83, 6558, 3279, 1093,
1192464, 596232, 298116, 149058, 74529, 24843, 8281, 1183, 169, 13] 84, 2, [84, 42, 21] 85, 1, [85, 17] 86, 6, [86, 43, 1764, 882, 441, 147,
49] 87, 1, [87, 29] 88, 3, [88, 44, 22, 11] 89, 1, [89, 7388] 90, 2, [90, 45, 15] 91, 1, [91, 13] 92, 2, [92, 46, 23] 93, 1, [93, 31] 94, 20+,
[94, 47, 2022, 1011, 337, 111548, 55774, 27887, 353, 123198, 61599, 20533,
421357694, 210678847, 44385566460664754, 22192783230332377, 1707137171564029,
165918667661, 27529004277737692540278, 13764502138868846270139,
4588167379622948756713, … ?] 95, 1, [95, 19] 96, 1, [96, 48] 97, 20+,
[97, 8634, 4317, 1439, 2062088, 1031044, 515522, 257761, 36823, 1601,
2556798, 1278399, 426133, 1187, 1401848, 700924, 350462, 175231, 25033,
626601024, 313300512, …?] 98, 1, [98, 49] 99, 1, [99, 33] 100, 1, [100, 50] |
|
|
||
|
Trajectoire pour les nombres de
2000 à 2030 Arrêt si le nombre est déjà dans une suite
précédente; cas repérés à partir de 2020. Nombreux nombres avec arrêts au-delà de 20
itérations: 2003, 2005, 2007, 2011, … |
2000, 16, [2000, 1000, 500, 250,
125, 25, 5, 16, 8, 4, 2, 7, 36, 18, 9, 3, 7] 2001, 17, [2001, 667, 29, 668, 334, 167, 27222, 13611, 4537, 349,
121104, 60552, 30276, 15138, 7569, 2523, 841, 29] 2002, 6, [2002, 1001, 143, 13, 144, 72, 36] 2003, 20+,
[2003, 4003998, 2001999, 667333, 445325324894, 222662662447, 7678022843,
58952034731561665592, 29476017365780832796, 14738008682890416398,
7369004341445208199, 1203888962823919, 2981170249, 8887375928313571544,
4443687964156785772, 2221843982078392886, 1110921991039196443,
65348352414070379, 2253391462554151, 60902471960923, 452480159] 2004, 3, [2004, 1002, 501, 167] 2005, 20+,
[2005, 401, 159198, 79599, 26533, 2041, 157, 23708, 11854, 5927, 35105622,
17552811, 5850937, 95917, 9199495388, 4599747694, 2299873847, 2163569,
4680983219244, 2340491609622, 1170245804811] 2006, 19, [2006, 1003, 59, 3128, 1564,
782, 391, 23, 438, 219, 73, 5184, 2592, 1296, 648, 324, 162, 81, 27, 9] 2007, 20+,
[2007, 669, 223, 47054, 23527, 3361, 11289600, 5644800, 2822400, 1411200,
705600, 352800, 176400, 88200, 44100, 22050, 11025, 3675, 1225, 245, 49] 2008, 19, [2008, 1004, 502, 251,
60492, 30246, 15123, 5041, 71,
4758, 2379, 793, 61, 3600, 1800, 900, 450, 225, 75, 25] 2009, 6, [2009, 287, 41, 1518, 759, 253, 23] 2010, 8, [2010, 1005, 335, 67, 4088,
2044, 1022, 511, 73] 2011, 20+,
[2011, 4028034, 2014017, 671339, 450685311498, 225342655749, 75114218583,
25038072861, 8346024287, 4608517, 21238318334882, 10619159167441,
965378106131, 3411230057, 2958569, 8753112776348, 4376556388174,
2188278194087, 128722246711, 336089417, 559217] 2012, 20+,
[2012, 1006, 503, 250998, 125499, 41833, 3803, 14439992, 7219996, 3609998,
1804999, 257857, 66485075310, 33242537655, 11080845885, 3693615295,
738723059, 38880161, 306143, 787, 608352] 2013, 2, [2013, 671, 61] 2014, 20+,
[2014, 1007, 53, 2492, 1246, 623, 89, 7388, 3694, 1847, 3381858, 1690929,
563643, 187881, 62627, 3921514860, 1960757430, 980378715, 326792905,
65358581, 1519967] 2015, 3, [2015, 403, 31, 900] 2016, 7, [2016, 1008, 504, 252, 126,
63, 21, 7] 2017, 16, [2017, 4056188, 2028094,
1014047, 44089, 1943751744, 971875872, 485937936, 242968968, 121484484,
60742242, 30371121, 10123707, 3374569, 306779, 27889, 167] 2018, 20+,
[2018, 1009, 1005974, 502987, 26473, 1151, 1299480, 649740, 324870, 162435,
54145, 10829, 1547, 221, 17, 222, 111, 37, 1148, 574, 287] 2019, 20+,
[2019, 673, 444854, 222427, 641, 404472, 202236, 101118, 50559, 16853, 887,
783222, 391611, 130537, 11867, 140778222, 70389111, 23463037, 1804849, 7489,
56070144] 2020, 7, [2020, 1010, 505, 101,
9798, 4899, 1633, 71] 2021, 20+,
[2021, 47, 2022, 1011,
337, 111548, 55774, 27887, 353, 123198, 61599, 20533, 421357694, 210678847,
44385566460664754, 22192783230332377, 1707137171564029, 165918667661,
27529004277737692540278, 13764502138868846270139, 4588167379622948756713] 2022, 1, [2022, 1011] 2023, 2, [2023, 289, 17] 2024, 3, [2024, 1012, 506, 253] 2025, 2, [2025, 675, 225] 2026, 20+,
[2026, 1013, 1022118, 511059, 170353, 29019803904, 14509901952, 7254950976,
3627475488, 1813737744, 906868872, 453434436, 226717218, 113358609, 37786203,
12595401, 4198467, 1399489, 199927, 28561, 2197] 2027, 20+,
[2027, 4088460, 2044230, 1022115, 340705, 68141, 4641287934, 2320643967,
773547989, 103457, 10702730108, 5351365054, 2675682527, 382240361,
146107678287795882, 73053839143897941, 24351279714632647, 3478754244947521,
3744622438049, 367949537, 135386850740028260] 2028, 4, [2028, 1014, 507, 169, 13] 2029, 7, [2029, 4112784, 2056392,
1028196, 514098, 257049, 85683, 28561] 2030, 3, [2030, 1015, 203, 29] |
|
|
|
||
|
Nombres
dont la trajectoire nécessitent plus de 30 itérations. Sans tenir compte des nombres rencontrés dans les
suites précédentes. |
47, 53, 68,
79, 89, 94, 97, 102, 103, 106, 113, 136, 137, 141, 149, 153, 157, 158, 159,
163, 170, 173, 178, 179, 188, 194, 197, 204, 206, 212, 226, 233, 235, 237,
238, 239, 255, 257, 265, 267, 269, 272, 274, 277, 281, 282, 283, 291, 293,
298, 306, 309, 311, 314, 316, 317, 318, 326, 329, 337, 339, 340, 346, 347,
353, 356, 357, 358, 367, 371, 373, 374, 376, 379, 383, 388, 394, 395, 397,
401, 408, 411, 412, 419, 423, 424, 425, 431, 439, 442, 445, 447, 449, 452,
457, 459, 466, 467, 470, 471, 474, 476, 477, 478, 479, 485, 487, 489, 491,
499, 503, … |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/SyraGene.htm
|
![]()