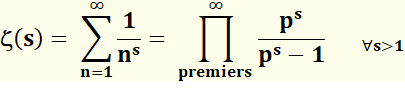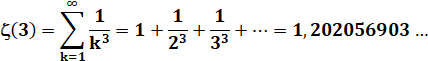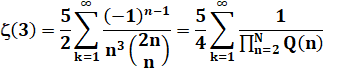|
||||||||||||||||||||||||||||||||
![]()
|
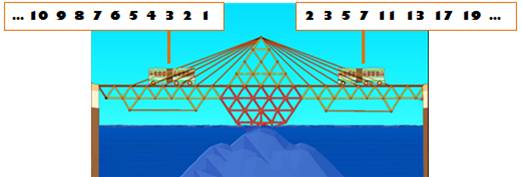
IDENTITÉ d'EULER Euler a découvert
une relation qui relie d'un côté les nombres
entiers et de l'autre les nombres
premiers. Un pont magique entre deux mondes si différents!
|
Voir Euler
|
|
|
|
Formulation
|
|
|
Lecture de
l'identité
Pour la valeur s = 1, il s'agit de la suite
harmonique qui est divergente. Lecture
abrégée
Expression en
anglais
|
|
Voir Relation
d'Euler avec les partitions
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Identité
Ou, écrit autrement:
Voir Somme des inverses des carrés - Démo Convergence Voici le calcul des premiers termes de
l'identité pour le cas des carrés:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
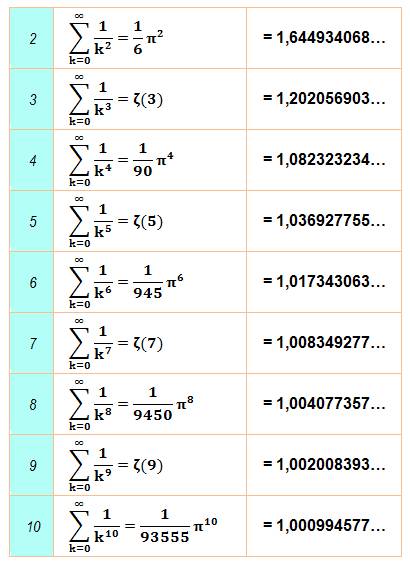
La fonction Voici quelques autres valeurs, avec 100 décimales
Somme
des inverses des puissances
Voir Somme suites infinies
/ Somme
des entiers, inverses … / Démonstration |
|
Zêta 2
|
Le
calcul de zêta (2) = pi/6,
dit problème de Bâle, est dû à Euler en 1735. Voir Démonstration |
|
En
1979, Roger Apéry a montré que ce nombre est irrationnel. Écriture
d'Apéry:
En
1998, sa valeur était connue avec 32 militions de décimales (Sebastian Wedeniwski – 35 heures de
travail). En
2017, connue avec 500 milliards de décimales (Ron Watkins) |
Voir Nombre 1,2020…
/ Historique de Zéta
Ce qui est connu
|
Pour tout entier k le quotient La somme La nature de la somme On sait que
On ne sait pas si |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Site |
|
|
Cette page |
![]()