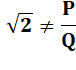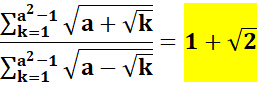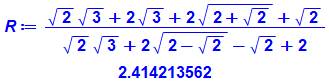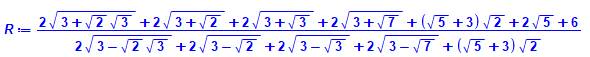|
||||||||||||||||||||||||||||
![]()
|
|
||
|
Irrationnel |
Aucune
fraction ne permet de donner racine de deux exactement. |
|
|
Algébrique |
Entier algébrique. Solution de l'équation
x² – 2 = 0 Équation
du deuxième degré. Irrationnel
de degré 2 ou irrationnel quadratique. |
|
|
Tr |
NON, puisque algébrique. |
|
|
Norm |
On ne sait pas si les chiffres des décimales sont
répartis selon la même fréquence. En
base 10 comme pour toute autre base. |
|
|
Formules |
Réduites, fractions continues, développements … |
|
|
Pell |
Numérateurs et dénominateurs forment une suite
d'équations de Pell |
|
|
Nombre
d' |
1 + √2 |
|
|
|
|
|
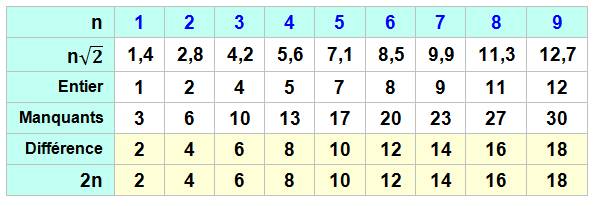
On écrit les multiples de On écrit dessous, et à la suite les uns des
autres, les nombres manquants dans la liste du haut. La différence
dans chaque colonne n est égale à 2n.
|
|
|
|
||
|
Entier algébrique: nombre réel ou
complexe, solution (ou racine) d'une équation polynomiale de degré
quelconque, dont tous les coefficients sont des nombres entiers, et dont le
coefficient du terme de plus haut degré vaut 1. |
Solution de: x² – 2 = 0 est un entier algébrique.
Solution de: 2x²
– 3 = 0 n'est pas un entier algébrique.
Solution de: x² +1 = 0 est un entier algébrique. |
|
|
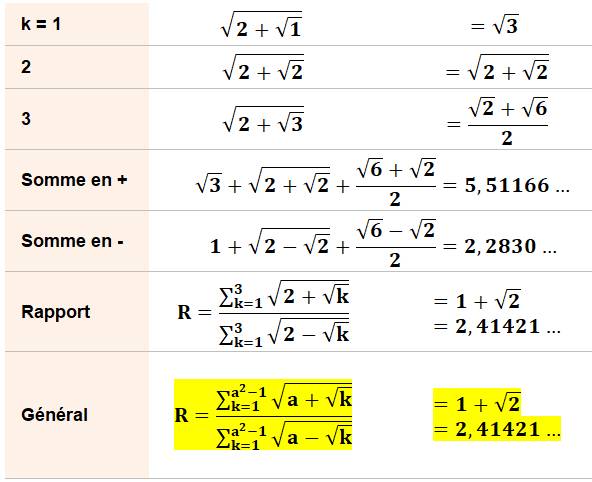
Cette
fraction avec des sommes conjuguées au numérateur comme au dénominateur est
une constante quelle que soit la valeur de a supérieure à 1. Je
ne connais pas le démonstration. |
|
|
|
Valeurs littérales pour a de 2 à 4
|
||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Diconombre |
|
|
Livre |
|
|
Cette page |
![]()