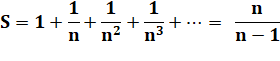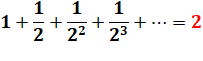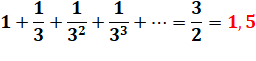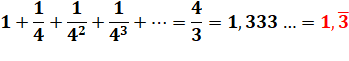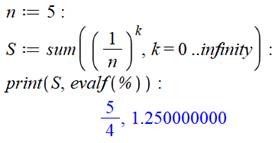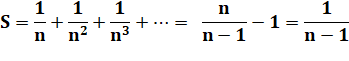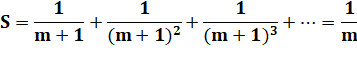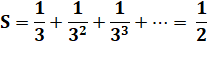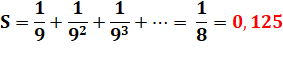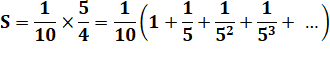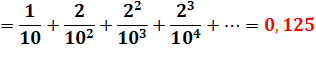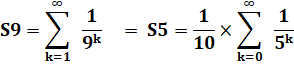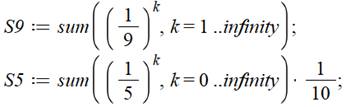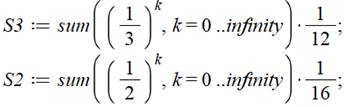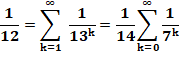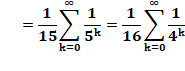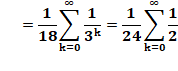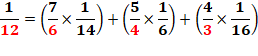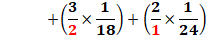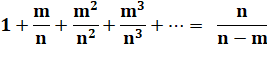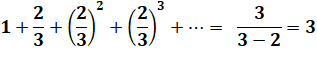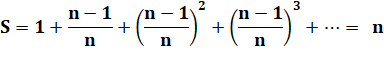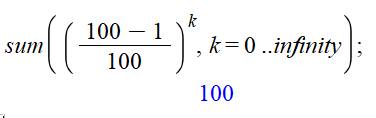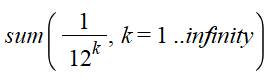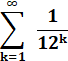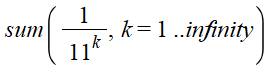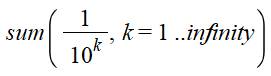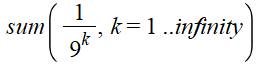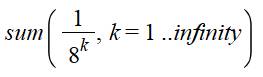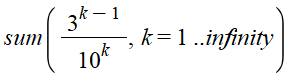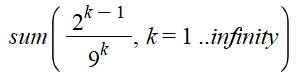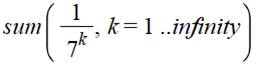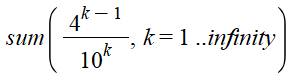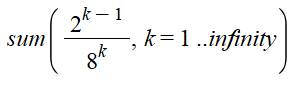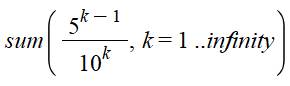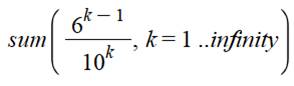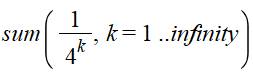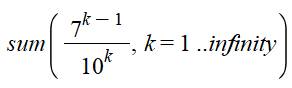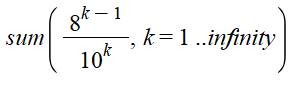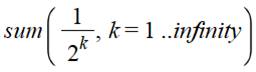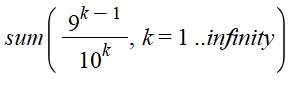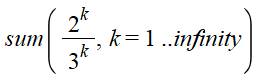|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PÉRIODIQUES En
tant que limite de séries Comment une somme
infinie (série)
produit un nombre décimal ou un nombre périodique. Exemples
Lecture
de la première formule: la somme,
depuis k égal un et jusqu'à k tendant vers l'infini, de la fraction un sur
onze à la puissance k est égale à un
dixième, soit zéro virgule un. On aura ainsi la somme infinie qui commence
par: 1/11 + 1/112
+ 1/113 … = 0,09090…+ 0,00826… + … = 0,0999… = 0,1 |
Voir Brève
de maths n°179
|
|
||
|
Somme des inverses des puissances
d'un nombre. |
|
|
|
Somme des
inverses des carrés. |
|
|
|
Somme des
inverses des cubes. |
|
|
|
Somme des
inverses des puissances 4. |
|
|
|
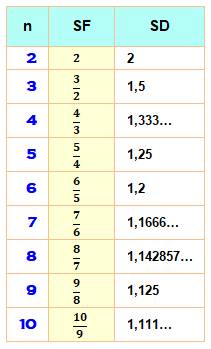
La
somme infinie S des puissances de l'inverse d'un nombre n est égale à la fraction
n / (n – 1) . |
||
|
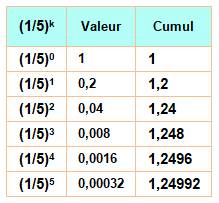
Exemples Lecture: la somme des inverses des puissances de 5 est égale à 1,25
|
Confirmation sous Maple:
L'instruction
somme (sum) exécute la somme de (1/n)k pour toutes les valeurs de
k de 1 à l'infini. Exemple avec les premiers calculs
|
|
|
|
||
|
En
retranchant un à la formule précédente. |
|
|
|
En
changeant de variable: m = n – 1. |
|
|
|
Toute
fraction en 1/m est la somme infinie des
inverses de 1 /(m + 1).
|
||
|
Exemples avec 1/2
avec m = 2 avec 1/8
avec m = 9 |
|
|
|
Notez que 0,125 =
1,25 / 10 Ce qui nous
ramène à la formule vue plus haut |
=> Deux possibilités pour
exprimer 0,125 = 1/8, en neuvièmes ou en dixièmes. |
|
|
La différence
entre les deux expressions est sans doute plus explicite avec cette écriture.
Notez la valeur initiale de k. Toutes les possibilités. Elles
résultent du calcul suivant:
|
Ou sous forme Maple
|
|
|
Évidemment
1/8 n'est pas une exception. On retrouve de multi présentations pour d'autres
nombres. Exemple avec 1/12 = 0,08333
|
|
|
|
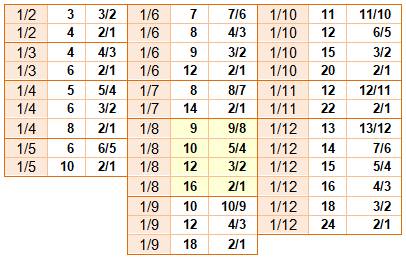
Ce qui se cache! Ces
égalités de sommes infinies résultent des égalités indiquées à droite. Les
nombres en rouge sont les diviseurs de 12. On les retrouve le plus à droite
de chaque groupe de colonne. |
L'inverse d'un nombre n est k fois la somme infinie des
puissances d'une fraction. La valeur de k étant la quantité des diviseurs de
n. |
|
Voir Nombre
0,125 / Nombre
0,08333…
|
|
||
|
Somme
infinie de raison m/n. |
|
|
|
Somme
infinie des puissances de 2/3: |
|
|
|
Avec m =
n – 1 |
|
|
|
Tout nombre entier n est la somme infinie des puissances de la fraction (n – 1) / n. On
retrouve bien le cas S = 2 avec la fraction (2 – 1) / 2 = 1/2. Le
logiciel Maple permet le calcul de vérification, comme par exemple avec S =
100:
|
||
![]()
|
|
|||
|
0,090909… |
|
Autre façon d'écrire:
|
|
|
0,1 |
|
|
|
|
0,111… |
|
|
|
|
0,125 |
|
|
|
|
0,142587… |
|
|
|
|
0,1666… |
|
|
|
|
0,2 |
|
|
|
|
0,25 |
|
|
|
|
0,333… |
|
|
|
|
0,5 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycSer.htm
|
![]()