|
Édition du: 19/10/2022 |
|
INDEX |
Nombres premiers – CRIBLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Types de CRIBLES
Un crible
destiné à isoler les nombres
premiers est un algorithme
de tri qui élimine progressivement les nombres
composés pour ne garder que les nombres premiers. Revue des
principaux cribles et accès vers leurs développements et programmation. Ces
algorithmes visent à connaitre tous les nombres premiers de 2 à une limite n. Une autre préoccupation consiste à déterminer si un
nombre n est premier (sans forcément connaitre la nature de ses voisins).
C'est l'objet des tests de
primalité. Une autre
idée, vaine à ce jour, consiste à trouver des formules
qui encapsuleraient un maximum de nombres premiers. |
||
|
|
Sommaire de cette page >>> Le crible le plus connu – Ératosthène >>> Divisibilité par 2, 3, et 5 >>> Divisibilité par 6 et 30 >>> Divisibilité par 4, 6, 12 et 60 >>> Optimisation >>> Bilan |
Débutants Glossaire |
|
À partir de
la liste des nombres (cubes rouges en haut); Une
grille qui est percée toutes les deux positions bloque les nombres pairs. La grille
suivante bloque les multiples de 3. Le nombre
4 a déjà été bloqué, on passe donc au 5. Etc. |
Les nombres premiers sont ceux qui subsistent en
tête de grille: 2, 3, 5, 7, 11 … Avec le 7, par exemple, on sait que le prochain
nombre retenu par la grille sera 7 x 7 = 49, car les précédents (2x7 = 17,
3x7 = 21 et 5x7 = 35) ont déjà été retenus sur les grilles supérieures avec
les nombres premiers: 2, 3 et 5. |
|
|
Le crible d’Ératosthène imagé par
une succession de grilles judicieusement percée
Voir Crible d'Ératosthène |
||
Crible produisant tous les
nombres premiers jusqu'à 121 = 11² (celui-ci étant composé !)

Il y a 30 nombres premiers de 1 à 121: 2, 3,
5, 7, 11, 13, 17, …113.
Les nombres
à droite indiquent la quantité de nombres retenus sur cet étage jusqu'à 121.
|
Réalisation par
programme |
|
|
Principe Le crible d'Ératosthène est facile à réaliser par programmation.
Cette méthode illustre bien le principe de
tamisage progressif, couche après couche. On observe également que certains nombres sont
analysés à plusieurs reprises, de couche en couche. Il est possible d'optimiser l'algorithme en réduisant certaines de ces
répétitions. Programme Maple
Explication détaillée de la
ligne 2:
|
|
Voir Programmation du crible
d'Ératosthène / Programmation – Index
|
Parmi tous
les nombres, il est facile d'éliminer ceux qui sont divisibles par
2 et par
5. Il suffit d'un simple test sur l'unité. Donc,
élimination de tous les nombres terminés par 0, 2, 4, 5, 6 et 8. |
Ce simple test élimine 60% des nombres. Ne restent donc que les nombres terminés en 1, 3,
7 et 9 (Voir la ligne du 7 ci-dessus). |
|
|
Un autre
écrémage facile à effectuer consiste à tester la somme des chiffres. Si elle
est divisible par 3, alors le nombre lui-même est divisible
par 3. Tous les
cribles s'empressent d'éliminer tous ces nombres avant de tester des
divisibilités plus difficiles à reconnaitre. |
Ce petit test élimine 16 % des nombres rescapés
du test précédent (n < 121). Ne restent alors que 32 nombres parmi les 121: |
|
|
En considérant
les nombres non divisibles par 2, 3 ou 5, on observe qu'ils sont tous voisins
d'un multiple de 6. |
Propriété Un nombre premier est toujours voisin d'un
multiple de 6 comme le montre cet exemple:
Voir Barre
magique des nombres premiers |
||
|
Un bon
moyen d'accélérer la recherche des nombres premiers consiste à ne considérer
que les multiples de 6 et à analyser les deux voisins. Voir Primorielle
et recherche des nombres premiers / Encore
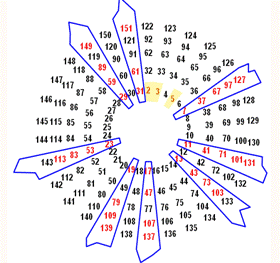
mieux, les examiner sur trois dizaines. En effet, avec 30 = 2 x 3 x 5, on
observe l'effet marguerite visible sur cette roue à huit pétales spécifiques
(languettes bleues). Chacun des pétales est voisin de pétales avec multiples
de 6:
Cette
propriété est exploitée pour réaliser le crible de la
roue (wheel sieve). Seuls les nombres des pétales sont à examiner. |
Propriété Sur une marguerite à 30 pétales seuls 8 sont susceptibles
de contenir des nombres premiers (à partir de 7). Elles sont voisines de pétales contenant des
multiples de 6.
|
||
Voir Brève
818
Arithmétique modulaire: on
se contente des restes …
|
La notion de divisibilité
est fondamentale pour la recherche des nombres premiers. On note, qu'il est
inutile de connaitre le résultat de la division.
Seul le reste importe. S'il est nul, le nombre est divisible donc non
premiers. Ce besoin limité a conduit à développer une
branche de la théorie des nombres dite arithmétique
modulaire. Dire que le nombre 19 est "égal" à 5 modulo 7, veut
dire que l'on retire le plus possibles de modules égaux à 7 dans 19 et que
l'on conserve uniquement ce qui reste: |
|
Pour
améliorer encore la vitesse de recherche, il faut faire appel à des
propriétés profondes de la théorie des nombres. Trouvé autour
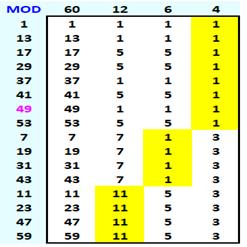
de l'an 2000, le crible d'Atkin est de ceux-là. Ce
mathématicien a divisé les nombres premiers en trois ensembles selon leurs
restes dans la division par 4, 6 ou 16 (Tableau). Pour
chacun de ces ensembles, il existe une propriété qui est spécifique des
nombres premiers. Le crible ramasse aussi des nombres comme les carrés (49 =
7²) qu'il suffit de retirer. |
Propriété Par exemple, le nombre 17 divisé par 60 donne un
reste de 17, par 12, un reste de 5, comme par 6 et il produit un reste égal à
1 lorsque divisé par 4. On note: 17 ≡ 1760 ≡ 512
≡ 56 ≡ 14
|
|
|
Nous avons
vu que l'algorithme de base du crible d'Ératosthène nécessite de reprendre
les tests de divisibilité à de nombreuses reprises pour certains nombres,
surtout lorsque ceux-ci deviennent grands. La
première idée, on l'a vu, consiste à réduire le champ d'analyse: crible de la roue |
Certains algorithmes tentent d'éliminer un
maximum de répétitions: cas du crible de Marouane Rhafli .
Cet algorithme exploite la propriété que tout nombre composé impair est de la
forme: n = p² + 2pk. Ex: 99 = 3² + 3 x 30 D'autres vont chercher des propriétés tout aussi
subtiles de la théorie des nombres:
|
|
|
Les algorithmes de cribles nécessitent la mise en
mémoire de tous les nombres premiers, ce qui limite leur intérêt dans le cas
de très grands nombres du fait de disposer de mémoires de très grandes
tailles. Le travail sur ces algorithmes reste un très bon
exercice d'apprentissage de la programmation. Il existe encore des recherches d'optimisation,
mais l'accent porte davantage sur la recherche de nombres premiers
très grands car utilisés par les méthodes de cryptage. Aujourd'hui de nombreux outils logiciels sont
disponibles pour indiquer rapidement la primalité d'un nombre. Voir aussi mes tables |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |