|
||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|||
|
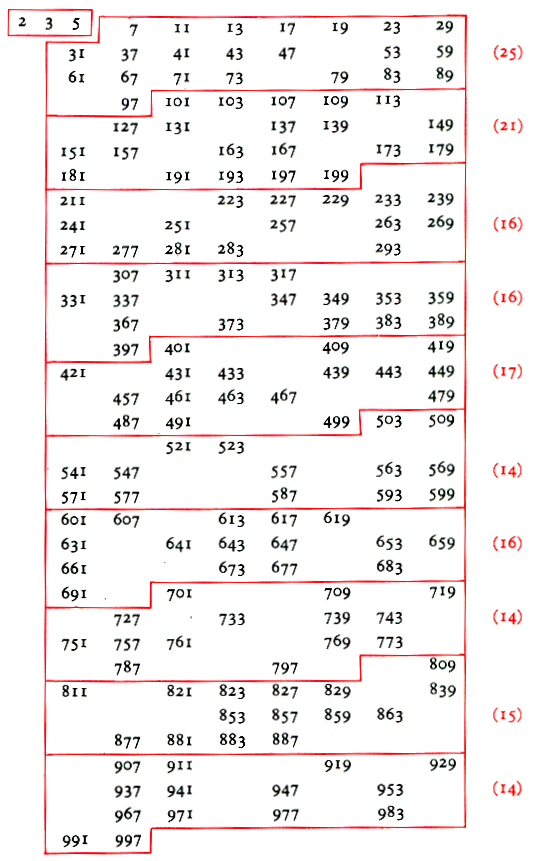
Théorème
P = 30 k + {1, 7, 11, 13, 17, 19,
23, 29} Attention:
la réciproque n'est pas vraie. Voir
les trous dans le tableau ci-dessous. |
Tableau pour n < 1000 Tous les
nombres sont placés en tableau avec:
Notez que le nombre
30 est le produit 2 x 3 x 5. Remarquez que dans chaque colonne:
|
||
|
|
|
Vérification
autour de 10 millions
|
|
|
||
|
On note
n# la primorielle
de n, qui est le produit des nombres premiers inférieurs à n ou égal à n. Tous les nombres
plus grands que n# sont évidemment de la forme n#. k + i pour i prenant
toutes les valeurs inférieures à n#. Certaines
valeurs de i conduisent à des nombres composés facilement reconnaissables. |
Avec 6#,
par exemple, on a 6# = 2 x 3 x 5 = 30. Or, tout
nombre est de la forme 30k + i avec i = {0, 1, 2, 3…, 29}. Tous ceux
avec i divisible par 2, 3 ou 5 sont composés. Pour
qu'un nombre soit premier, il ne reste que i = {1, 7, 11, 13, 17, 19, 23,
29}. Ce sont
d'ailleurs les nombres i tels que PGCD (1, 30) = 1;
autrement dit: i est premier avec 30. Bilan: tous les
nombres premiers sont de la forme 30k + i avec i = {1, 7, 11, 13, 17, 19, 23,
29}. Mais tous les nombres de cette forme ne sont pas premiers. |
|
|
La
généralisation est possible, cependant l'intérêt est vite limité. En effet
pour 10#, le paramètre i peut prendre 45 valeurs. |
Avec 10
#, 2 x 3 x 5 x 7 = 210 P = 210k
+ i i = {1,
11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157,
163, 167, 173, 179, 181, 191, 193, 197, 199}. |
|
Voir Brève
533
![]()
|
Voir |
|
|
|
|
|
Diconombre |
|
|
Cette page |
![]()