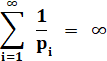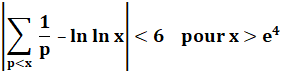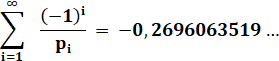|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres premiers Somme des inverses La somme des inverses des
nombres premiers du même type que celle des inverses des
nombres entier (série harmonique). |
Anglais:
the sum of the reciprocals of the prime numbers
|
|
|||
|
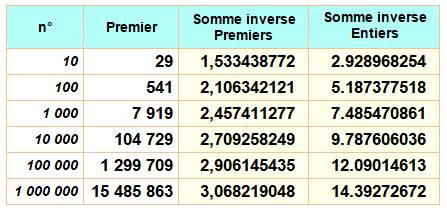
Quelques valeurs Le
dixième premier vaut 29 et la somme des inverses jusqu'à lui est égale à
1,53… Au
millionième premier qui vaut 15 485 863, la somme des inverses des premiers atteint
péniblement 3,068… Celle des inverses des entiers attient 14,392…. |
|
||
|
Divergence La
divergence de cette série a été prouvée par Euler en
1737 pour la première fois (Diverses
observations relatives aux séries infinies). Sa démonstration originale (aves les produits
d'Euler) est considérée comme la base de la théorie analytique des nombres. Il disait: cette somme progresse vers l'infini
moins vite que la série
harmonique. Elle varie comme le logarithme de celle-ci. |
|
||
|
Somme alternée des inverses des nombres premiers |
|
||
|
La
somme des inverses des nombres premiers dépasse le nombre 2 pour le 59e
nombre premier qui est 277. La valeur est 2, 002350… |
|||||
|
Valeur
de la somme |
0 |
1 |
2 |
3 |
4 |
|
Rang
du nombre premier |
1 |
3 |
59 |
361139 |
43922730588128390 |
|
Valeur
du nombre premier |
2 |
5 |
277 |
5195977 |
1801241230056600523 |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
![]()