|
|||||||||||||||||||||||||||||
![]()
|
Théorème des quatre couleurs Démonstration en bref Planches synthétiques
résumant la démonstration. Les explications plus précises se trouvent dans
les pages spécifiques. Voir l'index. La démonstration procède en
deux grandes étapes
La carte
à colorer est formée de régions ayant plus
ou moins de régions voisines. Une région spécifique entourée de ses voisines
est appelée configuration. |
|
|
|
|
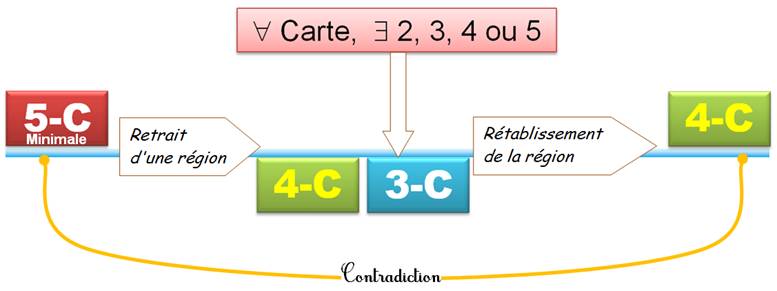
La
stratégie est basée sur une hypothèse qui finalement sera contredite. L'hypothèse: il existe des
cartes qui nécessitent cinq couleurs et, parmi elles, il y a celles qui
nécessitent juste les cinq couleurs. Autrement-dit: une seule région en moins
et la voilà 4-coloriable (4-C). Ce sont les 5-coloriables (5-C) minimales. Ensuite
vient une propriété valable pour toutes les cartes: elles contiennent toutes
une région avec 2, 3, 4 ou 5 frontières. La région et ses voisines forment
une configuration.
L'examen
de chacune de ces configurations réduite
d'une région montre qu'elles sont toutes 3-coloriables; de sorte que la
région retirée peut être réintégrée en lui donnant la quatrième couleur. Conclusion:
Cela
constitue l'essentiel de la démonstration initiale de
Kempe |
|
|
Cartes
Réduction
des configurations
Oups!
|
Suite Démonstration
de Kempe
|
|
|
|
Le
cœur de la démonstration consiste à monter que de toute manière une carte
contient certaines configurations inévitables et toutes ces configurations
conduisent à quatre couleurs seulement. Le
cas su pentagone est délicat et, finalement, se décline en des milliers de
configurations à examiner. Pour
conclure la démonstration, il faut donc:
Kempe
avait mis au point une géniale invention pour traiter le cas du carré et
croyait-il aussi le cas du pentagone. Dans la solution moderne, c'est la méthode
des charges de Heesch
qui va intervenir. Les sommets du pentagone sont chargés. On étudie
l'écoulement de ces charges vers les sommets voisins. On démontre que
certaines configurations doivent exister sinon les charges disparaitraient.
Pour venir à bout du problème, d'autres méthodes plus complexes furent
utilisées et programmées. La
démonstration complète est articulée en deux parties: 1.
Mise en action de tous les raisonnements possibles permettant
d'aboutir à un ensemble de configurations inévitables; et 2.
Exploration par ordinateur des cas les plus complexes. |
|
Suite
Démonstration
d'Appel et Haken
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Kempe.htm
|
![]()