|
|||||||||||||||||||||||||||||
![]()
|
Théorème des quatre couleurs Démonstration originale de Kempe La première démonstration
qui s'avéra fausse mais qui:
|
Voir Historique
|
|
||
|
|
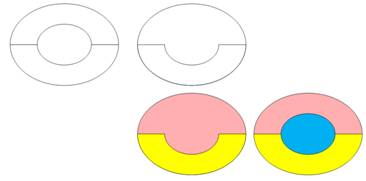
L'hypothèse est faite
qu'il faut cinq couleurs au plus. Un raisonnement conduit au fait que c'est contradictoire. Conclusion: il n'en faut que
quatre. |
|
|
|
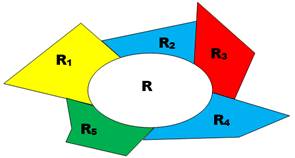
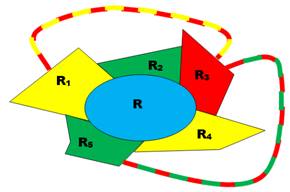
Il existerait des
cartes qui nécessitent cinq couleurs. Parmi toutes
celles-ci, intéressons nous à celles qui sont juste à la limite; celles qui,
si on retire une seule région, sont finalement colorables avec quatre
couleurs. Ce sont les cartes minimales En fait: des
contre-exemples du théorème des quatre couleurs. |
|
|
|
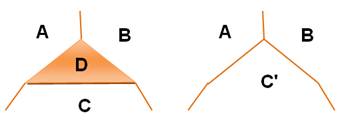
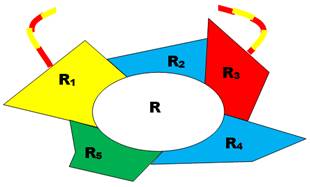
Une région est
momentanément réduite en un point.
S'agissant d'une carte minimale, lui ôter une région la rend 4-coloriable. L'idée est démontrer
qu'en réintégrant la région réduite, la carte reste
4-coloriable. C'est là qu'est la
contradiction. |
|
|
|
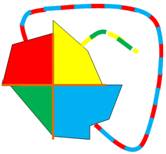
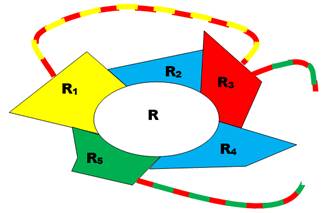
Il montre qu'il sait
opérer la réduction et produire une carte 4-coloriable Les cas 2, 3 et 4
côtés sont indiscutables. Il pensait avoir résolu le cas à 5 côtés qui va
s'avérer finalement très, très complexe.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
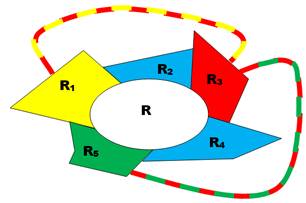
On montre, ici encore, qu'une carte hypothétique 5-coloriable minimale
ne peut pas comporter une telle région à quatre frontières. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Bilan Dans tous les cas (du moins
le pensait Kempe), une carte 5-coloriable minimale ne peut contenir une
région ayant cinq frontières. |
|
|
|
|
||
|
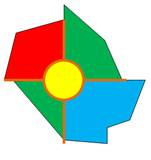
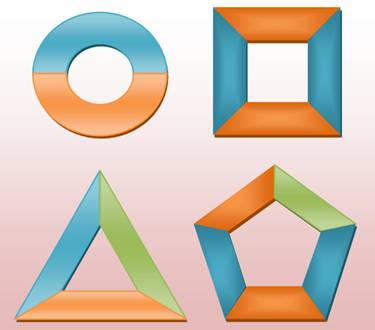
Théorème Dans toute carte, il existe au moins une région avec
cinq voisines ou moins. La région est en forme de cercle (2), de triangle (3),
de carré (4) ou de pentagone (5). Pour la résolution du problème des quatre couleurs, ces
cas sont des cas inévitables. |
|
|
Conclusion de Kempe
|
Toute
carte, fut-elle 5-coloriable, contient au moins une région ayant cinq
frontières ou moins. Un de ces cas est
inévitable. Or
une hypothétique carte 5-coloriable ne contient aucune des cinq
configurations. Cette
carte hypothétique n'existe pas. |
|
|
||
|
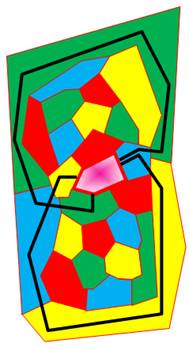
En haut à droite, identification de deux
chaines-circuits qui entraînent l'inversion des couleurs sur deux autres
chaines interrompues.
|
|
|
Simplification
|
Sans
encore avoir découvert l'erreur de Kempe, Peter Gunthrie
Tait tente de simplifier la démonstration. Elle toute aussi erronée, mais il introduit
la triangulation des cartes qui va servir par la suite. Si la nouvelle carte
est 4-coloriable, alors l'originale l'est aussi. Gunthrie appuyait sa
démonstration sur un lemme admis disant qu'une carte triangulée est
3-coloriable. ce qui est vrai. Mais, il n'avait pas conscience que ce lemme
est équivalent au théorème des quatre couleurs et donc aussi difficile à
prouver. |
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/DemoKemp.htm |
![]()