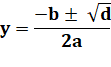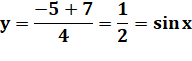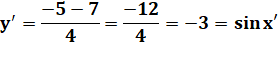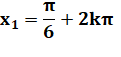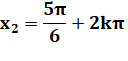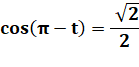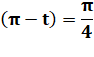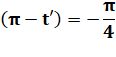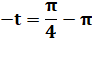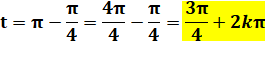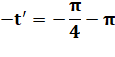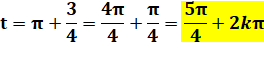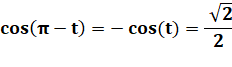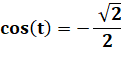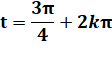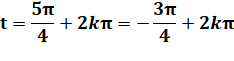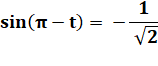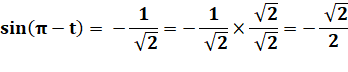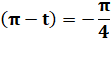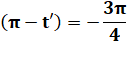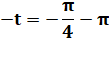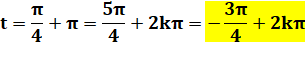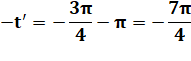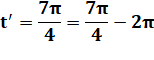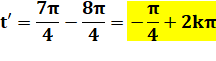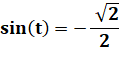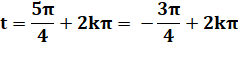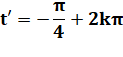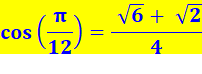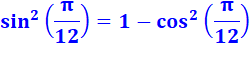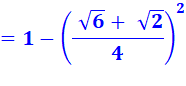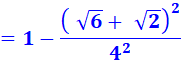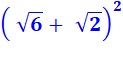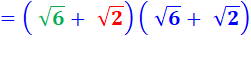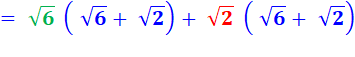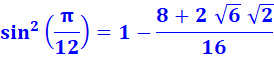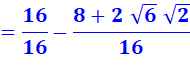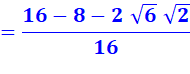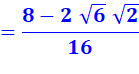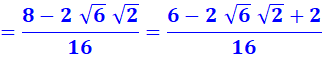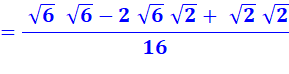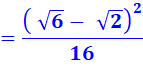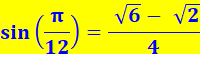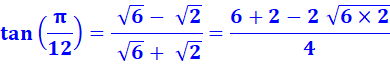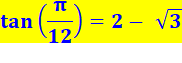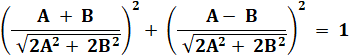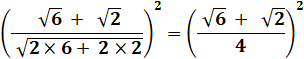NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/01/2024 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Analyse
Débutants Général	TRIGONOMÉTRIE				Glossaire Général
INDEX Trigonométrie ANALYSE	Débutant	Introduction	Angles	Valeurs
	Formules	Calculs simples	Angles orientés	Pi/5 = 36°
	Arctan	Calculs	Cosécante	Pi/2 = 90°
	Cours première	Exemple expliqué	Équations
	Première	Sommaire de cette page >>> Exercice 1 >>> Technique opératoire: équations >>> Exercice 2 >>> Exercice 3 >>> Égalité primordiale >>> Technique opératoire: racines >>> Sinus² + Cosinus² = 1

TRIGONOMÉTRIE – Équations

Je connais bien mon cours de première, je suis familiarisé avec le cercle trigonométrique et je viens de voir une équation simple en détail, alors je peux attaquer cette page d'exemples un peu plus compliqués.

Néanmoins, je voudrais me rassurer tout au long des calculs. Montrez-moi la technique opératoire en détail.

Exercice 1
Résoudre:	2 sin² (x) + 5 sin (x) – 3 = 0
Changement de variable pour y voir plus clair.	y = sin (x) 2y² + 5y – 3 = 0
Équation du deuxième degré.	ay² + by + c = 0 a = 2, b = 5 et c = –3
Discriminant. d = b² – 4ac	d = 25 – (4 x 2 x ( – 3)) = 25 + 24 = 49 = 7²
Solutions en y.
Solutions en x. La valeur absolue de y', supérieure à 1, ne correspond pas à un sinus.

Technique opératoire avec les équations

En premier: réflexe identités remarquables

sin² A – 4cos² A = ?

a² – b² = (a + b) (a – b)

sin² A – 4cos² A = (sinA + 2cosA) (sinA – 2cos A)

Etc. selon le problème posé

sin² X – 2sin X + 1 = 0

a² – 2ab + b² = (a – b)²

sin² X – 2sin X + 1 = (sin X – 1)² = 0

sin X – 1 = 0

sinX = 1

X = 0 + k

En second: on cherche les racines évidentes

sin² Y – 3 sin Y + 2 = 0

avec x = sin Y

x² – 3x + 2 = 0

Racines évidentes: 1 car: 1 – 3 + 2 = 0

& 2 car: 4 – 6 + 2 = 0

Se souvenir qu'un polynôme est exprimable en fonction de ses racines:

x² – 3x + 2 = (x – 1) (x – 2)

Puis retour à grand Y en écartant la racine 2 qui ne correspond pas à un sinus. Soit x = sin Y = 1 => Y =

Plus généralement si P est le produit des racines et S leur somme:

x² – Sx + P = (x – x₁) (x – x₂)

P = 1 x 2 = 2 et

S = 1 + 2 = 3

x² – 3x + 2 = (x – 1) (x – 2)

Essayons de deviner les solutions en utilisant cette technique:

x² – 8x + 15 = 0

Produit: 15 = 3 x 5 (ou 1 x 15, mais 1 n'est visiblement pas racine)

Somme: 8 = 3 + 5 (ça marche)

x² – 8x + 15 = (x – 3) (x – 5) = 0

Solutions: x = 3 et x' = 5.

Exercice 2
Résoudre
On considère (Pi – t) comme un tout dans sa parenthèse. Ne pas oublier la deuxième solution.
Mettons tous les Pi ensemble. En final, on n'oublie pas que l'angle est défini à un nombre de tours près.
Deuxième solution.
Remarque: nous aurions pu nous rendre compte tout de suite que:
Une simple lecture sur le cercle trigonométrique donne la réponse.

Voir Ce cas expliqué en détail

Exercice 3
Résoudre
On considère (Pi – t) comme un tout dans sa parenthèse.
Suppression de la racine au dénominateur avec l'aide d'une fraction unitaire.
Solutions.
Calcul de la première solution.
Calcul de la seconde solution.
Calcul de l'angle principal en retirant 2 Pi.
Remarque: nous aurions pu nous rendre compte tout de suite que
Une simple lecture sur le cercle trigonométrique donne la réponse.

Égalité primordiale
Du fait de la construction du sinus et du cosinus formant un triangle rectangle.
Exemple d'application: nous connaissons le cosinus d'un angle et nous voulons en déduire son sinus. Note: Pi / 12 = 180°/ 12 = 15°
Application de notre égalité.
Calculs et placement des parenthèses.
Calcul du carré au numérateur Je ne suis pas sûr de mon identité remarquable car je suis impressionné par les racines. Je refais le calcul complet. Je me souviens de la définition de la racine carrée qui multipliée par elle-même redonne le nombre: . Prenez pour vous en convaincre. Je pourrais faire . Prenez pour vous en convaincre. Mais je suspecte que je n'en ai pas besoin pour la suite.
Reprise du calcul du sinus. N'oublions pas que cette expression est un carré. il faut en trouver la racine.
C'est le développement du carré qui avait fait apparaître le produit de racine de 6 et de racine de 2. Cette puce à l'oreille, nous suggère de faire machine arrière et ainsi retrouver un carré.
Disposant d'un carré, nous pouvons en prendre la racine.
Calcul de la tangente de Pi/12 = 15°

Voir Lecture de ces valeurs sur le rectangle d'Ailles / Autres égalités fondamentales

Remarque de calcul sur cos² + sin² = 1

Avec un peu d'habitude, on se souvient que:

À mettre en relation avec la formule classique avec:

Or, la forme donnée en cosinus est bien conforme à cette relation

Conclusion: le deuxième terme cherché (le sinus) est bien le conjugué du premier.

On retient:

Bases	Trigonométrie – Débutant Trigonométrie – Introduction Trigonométrie – Tables
Voir	Angles Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés)
Aussi	Triangle Pentagone Identités remarquables
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Equation.htm