|
||||||||||||||||||||||||||||||||
![]()
|
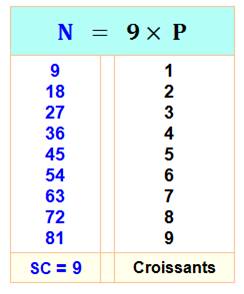
NOMBRES CROISSANTS, DÉCROISSANTS Ou Ascendants et descendants Définition: Nombres
dont les chiffres successifs vont en croissant: le suivant à droite est strictement
plus grand que le précédent. Propriété: En
multipliant un nombre croissant par 9, on obtient un produit dont la somme
des chiffres est strictement 9. Oui! Même avec ce grand
nombre:
Voir Brève
602 pour explications |
Anglais: numbers such that no digit is exceeded by the digit to
its left
|
|
||
|
Croissants
ou décroissants, ils sont en nombre infini. La logique de construction est
évidente (indiquée en rouge). Tous les chiffres
sont différents et chacun plus grand strictement que le précédent (ou plus
petit). |
||
|
Croissants 12, 13, 14, 15, 16, 17, 18, 19, 23, 24,
25, 26, 27, 28, 29, 34, 35, 36, 37, 38, 39, 45, 46, 47, 48, 49, 56,
57, 58, 59, 67, 68, 69, 78, 79, 89, 123, 124, 125, 126, 127, 128, 129, 134, 135, 136,
137, 138, 139, 145, 146, 147, 148, 149, 156, 157, 158, 159, 167, 168, 169,
178, 179, 189, 234, 235, 236, … |
Décroissants 10, 20, 21, 30,
31, 32, 40, 41, 42, 43, 50, 51, 52, 53, 54, 60,
61, 62, 63, 64, 65, 70, 71, 72, 73, 74, 75,
76, 80, 81, 82, 83, 84, 85, 86, 87, 90, 91, 92, 93, 94, 95, 96, 97, 98, 210, 310, 320, 321, 410, 420, 421, 430, 431, 432, 510, 520, 521, 530, 531, 532, 540, 541, 542, 543, 610, … |
|
|
En base 3: 5. En base 5: 7, 8, 9, 13, 14, 19, 38, 39, 44, 69, 194, … |
En base 3: 6, 7, 21. En base 5: 10, 11,
15, 16, 17, 20, 21, 22, 23, 55, 80, 85, 86, 105, 110, 111, 115, 116, 117,
430, 555, 580, 585, 586, … |
|
|
|
||
|
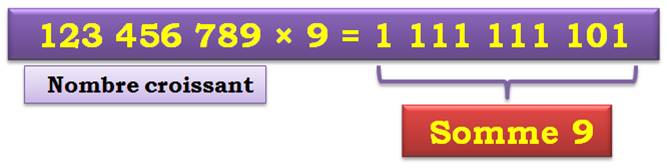
Le pannumérique croissant (123 456
789), multiplié par 9, donne un produit comportant neuf 1, soit une somme
égale à 9. Tronqué
par la droite, mais restant croissant, et multiplié par 9, la somme des
chiffres reste égale à 9. La somme
des chiffres reste égale à 9 même si on tronque par la gauche ou par les deux
bouts ou par le centre; pourvu que le nombre reste croissant. |
Tronqué par la droite
|
|
|
Tronqué par la gauche
|
Tronqué par les deux bouts ou par le centre
|
|
Voir Pépites numériques
|
|
|||
|
La table de multiplication du 9
est simple. Elle peut
se résumer à une soustraction: 8 x 9 = 80 – 8 = 72 On sait
aussi que la somme des chiffres est égale à 9. D'ailleurs,
pour tous les multiples de 9, la somme des chiffres est égale à 9 ou un
multiple de 9. C'est d'ailleurs la base de la preuve par neuf. Oui, mais
avec des nombres plus grands, on devrait avoir 18, 27 … |
|
||
|
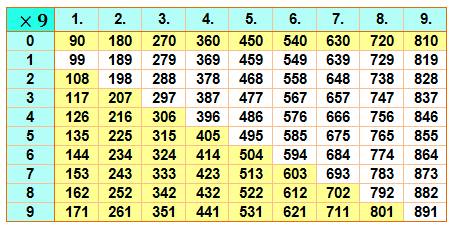
Sur cette table de multiplication par 9 des nombres
à deux chiffres, on a coloré en jaune les nombres dont la somme des chiffres
est exactement 9; les autres sommant en 18. Outre la première ligne avec unité nulle, on
remarque qu'il s'agit de tous les nombres dont le chiffre des unités est plus
grand que celui des dizaines: nombres croissants. |
|
||
|
|
|||
|
Observations Si la
propriété est intrigante, le pot-aux-roses est vite trouvé. On a vu
que multiplier par 9 revient à multiplier par 10 et à retrancher le nombre. Or, en multipliant
par 10, on décale tous les nombres d'un cran vers la gauche. En
faisant la soustraction 10N – N, les chiffres en haut et en bas sont les
mêmes, mais décalé d'un cran. Ceux du haut étant plus grands que ceux du bas
puisqu'il s'agit de nombres croissants Si bien
que pour tous les nombres sauf celui des unités, la différence ne produit pas
de retenue. |
|
||
|
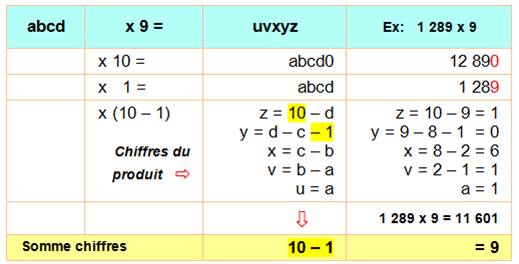
Formalisation Prenons le cas d'un nombre à quatre chiffres; il
sera évident de prolonger à neuf chiffres; le plus grand nombre croissant
étant 123 456 789. Avec la notation des chiffres, on calcule chaque chiffre
du résultat en tenant compte de la seule retenue pour les unités. La somme de ces chiffres est réduite à l'effet
des retenues (10 – 1), les autres chiffres s'annulent. |
La somme des chiffres du
produit est égale à 9. |
||
|
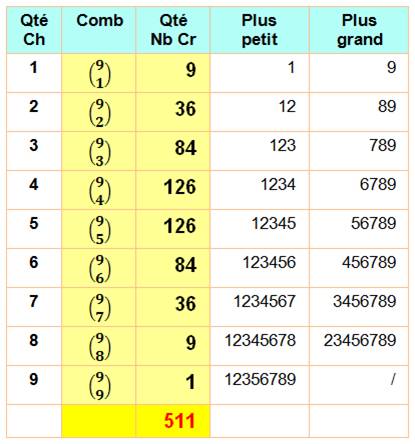
La somme des chiffres d'un nombre croissant multiplié par
9 est strictement égale à 9. Les nombres
croissants sont en nombre limités. Il y en a 511 de 1
à 123 456 789 dont 9 triviaux.
Exemple de
dénombrement pour deux chiffres:
Avec trois
chiffres, on trouverait que: Q3
= somme de 1 à 8 plus somme de 1 à 7 plus … plus 1, soit
28 + 21 + 15 + 10 + 6 + 3 + 1 = 84. En
termes de combinaisons:
choix de 3 parmi 9
|
Anglais: How many k
digit numbers have their digits in increasing order?
How many k-digit numbers with strictly increasing
digits do exist?
|
|
|||
|
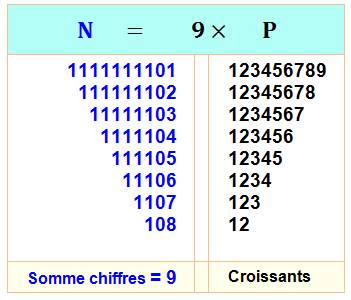
On prend
le plus petit nombre croissant et le plus grand; leur multiplication par 9
produit deux nombres, l'un étant le permuté de
l'autre. |
12 x 9 = 108 89 x 9 = 801 123 x 9 = 1 107 789 x 9 = 7 101 12345 x 9 = 111 105 56789 x 9 = 511 101 12345678 x 9 = 111
111 102 23456789 x 9 = 211
111 101 |
||
|
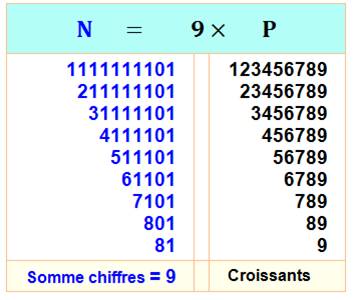
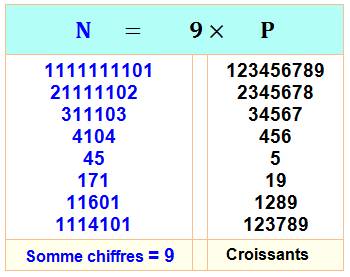
Les
chiffres de l'un sont les compléments à 10 des symétriques de l'autre. Soit, le calcul
indiqué dans ce tableau, avec exemple numérique en colonne de droite. |
|
||
|
|
|||||||||||||||||||||||||||||||||||
|
Nombres dont les chiffres se suivent et qui sont divisibles par 2, 3,
5, … Comme 98 = 7 x
14 Testé jusqu'à un
million.
|
|||||||||||||||||||||||||||||||||||
Voir
Barre
magique des nombres premiers / Nombres
pannumériques
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()