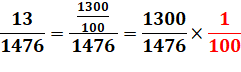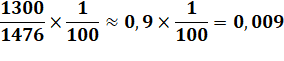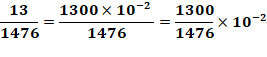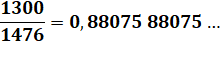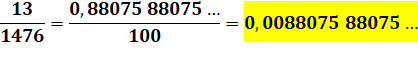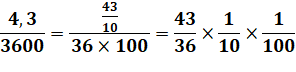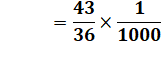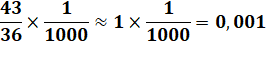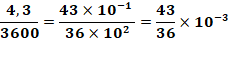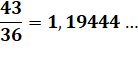Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 21/11/2023 M'écrire Brèves de Maths

INDEX Calcul	DIVISIONS
	Initiation	Avancé	Fractions	Décimales – Débutants
	Polynôme	Complexes	À l'envers	Décimales – Expérimentés
		Division rapide (dév. limités)		Tailles différentes
				Algorithmes de divisions

Faites un double-clic pour un retour en haut de page

Division entre nombres de tailles différentes Comment évaluer l'ordre de grandeur et effectuer la division posée ? Le calcul rapide de l'ordre de grandeur est une assurance de ne pas se tromper en annonçant le résultat.
	Sommaire de cette page >>> Division de nombres de tailles différentes – (1/2) >>> Division de nombres de tailles différentes – (2/2)	Débutants Nombres Glossaire Nombres

Calculer

Division de nombres de tailles différentes – (1/2)			haut
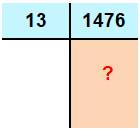
Première étape Donner aux deux nombres des tailles de même grandeur en multipliant et divisant par des puissances de 10. Le nombre 13 devient 133 en le multipliant par 100. On surestime alors le résultat d'un facteur 100. On devra donc diviser le résultat obtenu par 100.		Exemple Diviser 13 par 1476 Mise à l'échelle Ordre de grandeur
Pour les connaisseurs En utilisant les exposants des puissances de 10. Rappel: 10^2 = 100 et 10^-2 = 1/100
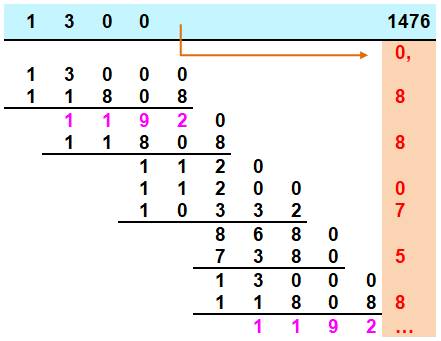
Deuxième étape Maintenant, la division devient classique: 1300 à diviser par 1476. Combien de fois 1476 dans 1300 ? zéro fois. En l'absence d'autres chiffres, j'abaisse un 0 et je m'en souviens en notant une virgule dans le résultat. Combien de fois 1476 dans 13000 ? Huit fois et reste 1192. … Le reste 1192 à déjà été trouvé plus haut. La suite est une répétition à partir de ce point.	Division posée
Troisième étape On recopie le résultat et on le divise par 100. Ce résultat est conforme avec l'ordre de grandeur prévu.

Division de nombres de tailles différentes – (2/2)		haut
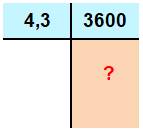
Première étape Donner aux deux nombres des tailles de même grandeur en multipliant et divisant par des puissances de 10. Le nombre 4,3 devient 43 en multipliant par 10 Le nombre 3600 devient 36 en divisant par 100. On surestime le résultat d'un facteur 10 × 100 = 1000. On devra donc diviser le résultat obtenu par 1000.	Exemple Diviser 4,3 par 3600 Mise à l'échelle Ordre de grandeur
Pour les connaisseurs En utilisant les exposants des puissances de 10.
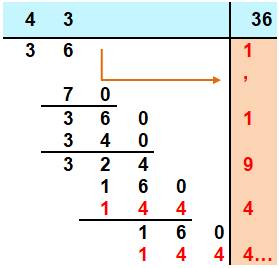
Deuxième étape Maintenant, la division devient classique: 43 à diviser par 36. Combien de fois 36 dans 13 ? Une seule fois et reste 7. En l'absence d'autres chiffres, j'abaisse un 0 et je m'en souviens en notant une virgule dans le résultat. Combien de fois 36 dans 70 ? Une seule fois et reste 34. … Le reste 144 est répété sans fin, ce qui veut dire que le 4 du résultat est lui aussi répété.	Division posée
Troisième étape On recopie le résultat et on le divise par 1000. Ce résultat est conforme avec l'ordre de grandeur prévu.

Haut de page (ou double-clic)

Retour	Division décimale – Approche
Suite	Division décimale à l'américaine Division de polynômes Division euclidienne (théorie) Racine carrée posée (à la main) Calcul complet de 1/19
Retour Voir résumé en: Très utile:	Initiation aux divisions Glossaire La preuve par neuf
Voir	Barre magiques des premiers Calcul mental – Index Carrés Magiques Conversion de fractions en nombres à décimales Débutants – Index Diviseur électronique Division par 10 Euros et divisions par 3 Fractions Jeux – Index Les quatre opérations – Junior Multiplication Partition des nombres de 1 à 10 Pascaline Plus et moins dans les multiplications Somme des chiffres Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/DivGdta.htm