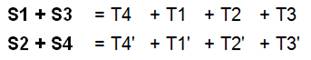|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
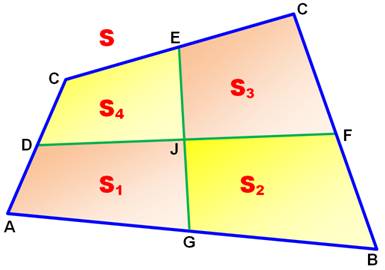
AIRE des QUADRILATÈRES formés par les bimédianes
Le but est de calculer les
aires S, S1, S2, S3 et S4 en fonction des coordonnées des quatre sommets. Occasion de résoudre une énigme qui consiste à calculer l'aire de la quatrième
surface connaissant les trois autres. Propriété
|
|
|
||
|
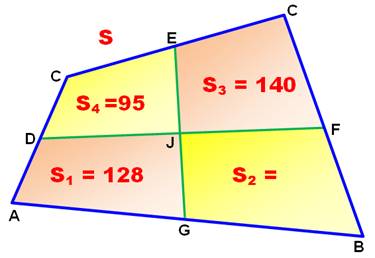
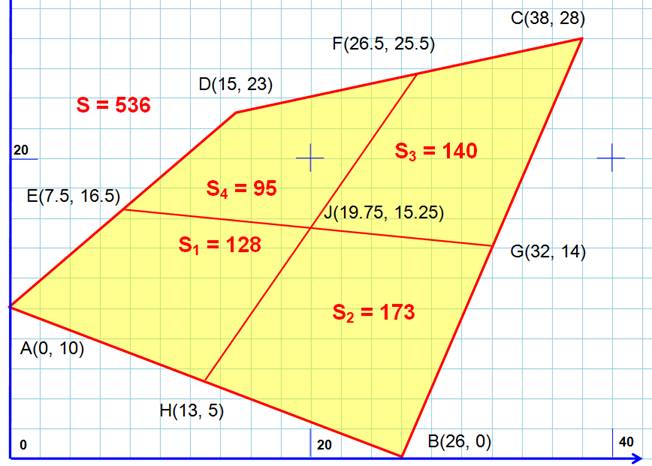
Énigme On donne un quadrilatère dont trois
surfaces sont connues (en cm²) comme indiqué. Les points E, F, G et H sont les milieux
des côtés (EG et DF sont les médianes). Trouvez la valeur de l'aire du quatrième
quadrilatère (S2). S1 + S3 = S2 + S4
= 128 + 140 = x + 95 x = 268 – 95 = 173 cm² et S = 268 x 2 = 536 cm² |
|
|
Voir Calcul des aires et
des coordonnées / Brève
911
Merci à Ivan F pour m'avoir communiqué ce problème
![]()
|
Formule des aires avec les
bimédianes |
|
|
|
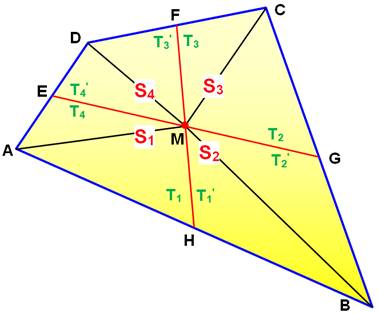
Un quadrilatère convexe quelconque: ABCD. Les deux médianes: EG et FH qui se coupent
en M. On partage chacun des quatre quadrilatères
ainsi formés en deux triangles. Les triangles AMH et HMB (T1 et T1')
ont un côté de même longueur (AH = HB) et une hauteur commune (issue de M,
non représentée); ils ont même aire. On écrit en abrégé: T1 = T1' De même pour les autres. Les couples
d'égalité sont mentionnées en vert. |
|
|
![]()
Travaux pratiques sur le calcul de l'aire du quadrilatère
|
|
|
|
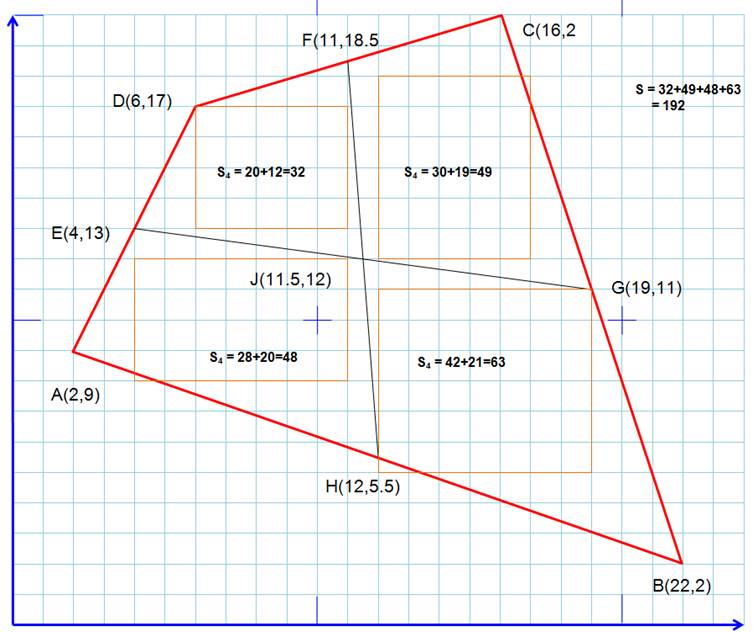
Exemple
de quadrilatère Le
quadrilatère convexe quelconque ABCD. Ses
médianes EG et FG dont les extrémités partagent les cotés en deux parties
égales. Les
coordonnées des
points sont renseignées avec le carreau pour unité. Les
aires sont évaluées en comptant la quantité de carreaux couverts.
Notez en passant que le quadrilatère EFGH
est un parallélogramme; ses
côtés sont parallèles, deux à deux, aux diagonales AC et BD du quadrilatère
initial. Voir Quadrilatère et médianes Formule
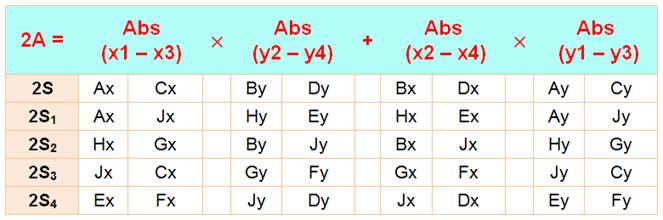
de l'aire du quadrilatère appliquée aux cinq surfaces
Application
numérique Pour le
calcul des différences, on prend la valeur du plus grand moins le plus petit
(autrement dit, la valeur absolue).
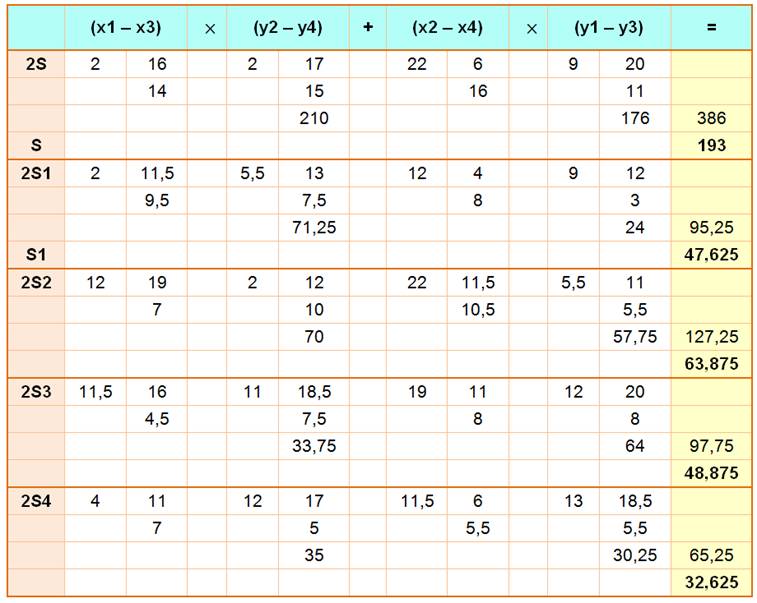
Observez
que les cinq valeurs sont très proches de celles estimées avec la quantité de
carreaux. Une
autre découverte, bien plus intéressante, peut être faite: S1 + S3 = 47,625 + 48,875
= 96,5 = 193 / 2 = S / 2 S2 + S4 = 63,875 + 32,625
= 96,5 = 193 / 2 = S / 2 |
|
![]()
Énigme – Solution
|
|
||
|
Énigme On
donne un quadrilatère dont trois surfaces sont connues (en cm²) comme
indiqué. Les
points E, F, G et H sont les milieux des côtés (EG et DF sont les médianes (ou plus
exactement les bimédianes). Trouvez
la valeur de l'aire du quatrième quadrilatère (S2) ainsi que les
paramètres du quadrilatère. |
|
|
|
Solution On reprend l'analyse avec coordonnées cartésiennes vue
ci-dessus. Sans perdre en généralité, on appuie le quadrilatère
sur les axes: Ax = 0 et By = 0. Reste six
coordonnées sur huit à trouver avec seulement trois valeurs connues. Ce qui
conduirait à un système de trois équations pour six inconnues. Cependant, les
deux médianes apportent des informations complémentaires. Les parcelles ont
des demi-médianes en commun. Nous savons que la solution est S2
= 173 cm². La figure
montre les sommets et les points milieux avec leurs coordonnées, trouvées par
exploration des solutions possibles (utilisation des formules vues ci-dessus
et calcul sur tableur ou avec Maple).
|
||
|
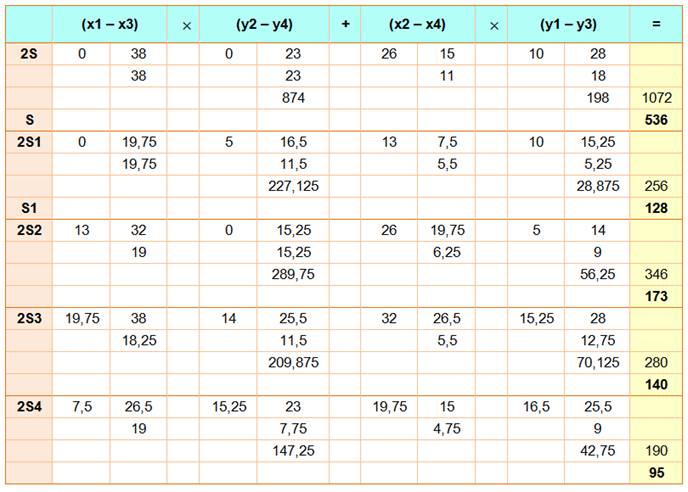
Calcul
de vérification
|
||
Bilan
|
L'énigme
de la quatrième parcelle est résolue. Elle fut l'occasion, en bonus, de
pratiquer le calcul de l'aire des quadrilatères quelconques. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()