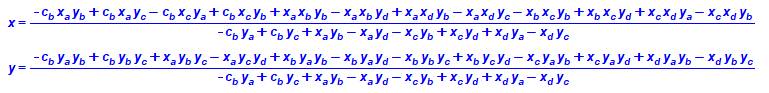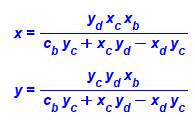|
Édition du: 26/06/2023 |
|
INDEX |
Quadrilatères |
||
|
Quadrilatère
– Introduction |
Quadrilatère – Aire |
||
Faites un double-clic pour un retour en haut de page
![]()
|
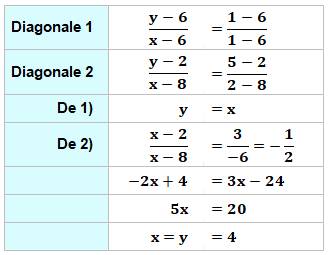
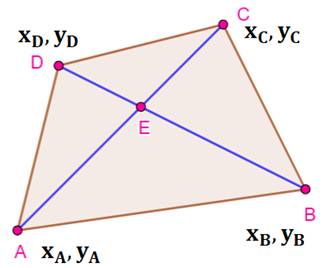
DIAGONALES du QUADRILATÈRE Comment
calculer les coordonnées du point d'intersection des diagonales du quadrilatère quelconque ? Solution: établir les équations des diagonales et chercher
le point commun en x et y. |
||
|
|
Sommaire de cette page >>> Approche – Cas simples >>> Exemple de quadrilatère >>> Rappel: équation de la droite >>> Cas général du quadrilatère quelconque |
Débutants Glossaire |
|
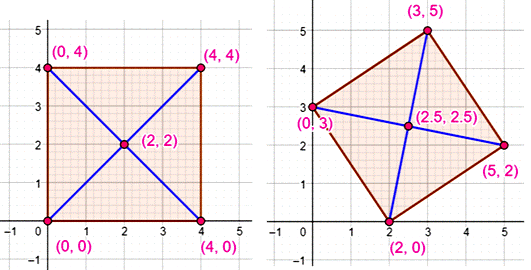
Dans le cas du carré, le calcul des coordonnées du
point d'intersection des diagonales est simple. Il s'agit simplement des moyennes des coordonnées
des sommets (somme divisée par 2). |
|
|
|
Évidemment, le calcul des moyennes ne marche
plus. Il faut recourir aux équations des deux diagonales et trouver les
coordonnées du point de concours.
|
|
|
|
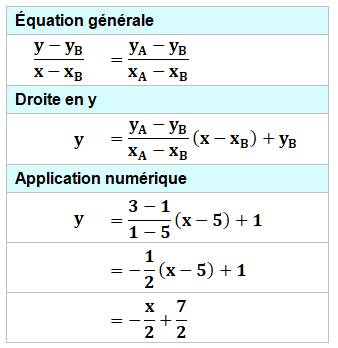
Équation
de la droite passant par A et B
|
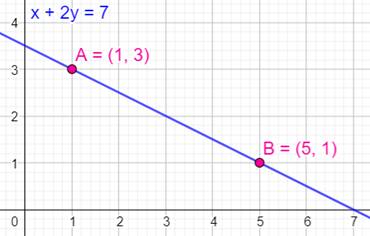
Exemple
de droite
Équation
de la droite x + 2y = 7
(donnée par le logiciel de dessin) ou 2y = 7 –
x Ou encore
y = 7/2 – x/2 |
|
Calcul avec coordonnées quelconques
Ces deux équations sont à résoudre selon les
valeurs numériques. Par exemple, calculer la valeur de y en fonction
de x dans l'une et reporter cette valeur dans l'autre. |
|
||
|
Pour
information, valeurs de x et y
|
|||
|
Point A
à l'origine (0, 0) |
|
||
|
Et point B sur l'axe des abscisses (x, 0) |
|
||
|
Exemple quadrilatère convexe
|
|
|
Exemple quadrilatère concave
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |