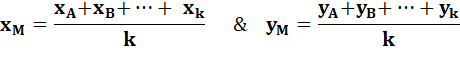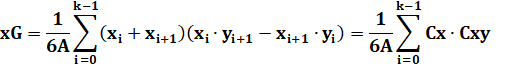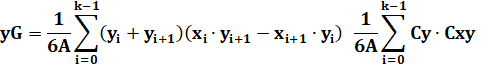|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
QUADRILATÈRE et ses MILIEUX Construction des "points milieux" du quadilatère:
centre géométrique et centres
de gravité (CG). Ne pas confondre
ces deux points ! |
Anglais: Center of quadrilateral / Quadrilateral centroid
|
|
||
|
Centres
de gravité (CG) du quadrilatère quelconque |
Il en existe trois qui, en général, ne sont pas
confondus: 1.
CG: Cas classique
en considérant toute la surface homogène: centre de gravité (de la surface). 2.
CG-côtés: Cas
d'un objet vide avec matérialisation seulement des quatre arêtes: centre de
gravité des côtés. 3.
CG-sommets: Cas
d'un objet immatériels avec seulement des masses égales aux quatre sommets:
centre de gravité des sommets. CG-sommets et CG-côtés sont confondus. |
|
|
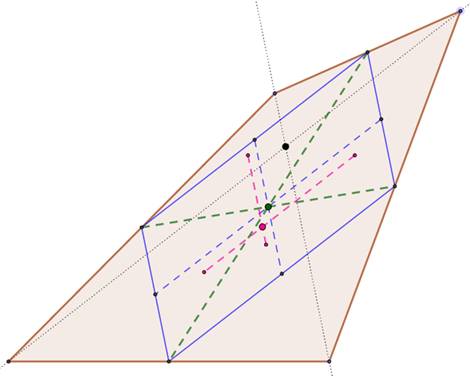
Trois points caractéristiques du
quadrilatère: NOIR: intersection des diagonales VERT: intersection des médianes du quadrilatère:
centre géométrique et CG des sommets, ROUGE: Centre de gravité du quadrilatère (CG de
la surface) – Construction en rouge, détaillée ci-dessous. |
|
|
Voir Point de concours des quatre médianes-hauteurs
|
Centre géométrique du
quadrilatère CG des sommets et CG des côtés |
|
||
|
Centre
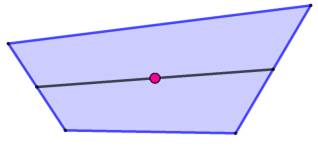
M du quadrilatère C'est le point de concours des médianes (vert). C'est aussi le milieu du segment qui réunit les
milieux des diagonales (rose). C'est le centre de gravité d'un objet vide ayant des
masses égales déposées aux sommets. C'est aussi le centre de gravité des côtés
considérés comme des "tubes" de masses identiques. |
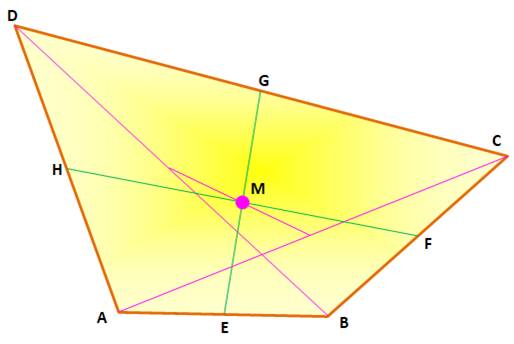
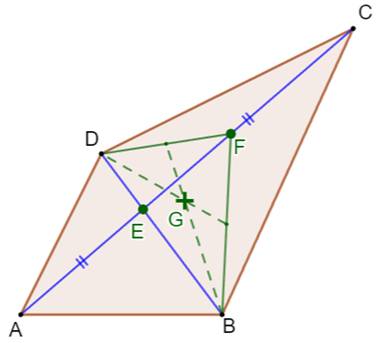
Rappel: le centre de gravité de quatre points de masses égales (A, B, C et D)
est situé à l'intersection de segments réunissant les points milieux (E, F, G
et H) deux à deux (M). |
||
|
Concernant les côtés Masses identiques ou masses quelconques ? |
Quatre côtés de masses
identiques Le CG du "tube" AB se trouve en E,
milieu AB. Idem pour les autres côtés. Le CG des quatre points E, F, G et H, formant un parallélogramme,
se trouve sur l'intersection de segments EG et FH, qui est aussi le point M. Quatre côtés de masses
quelconques Si les tubes on des masses différentes, la
recherche du centre de gravité se fera en appliquant les pondérations dues
aux masses. La masse de chaque tube est ramenée au centre du tube. On dispose
alors de quatre objets de masses différentes, situés en E, F, G et H dont il
faut calculer le centre de gravité. |
||
|
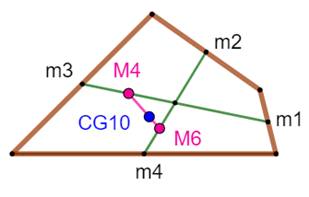
Exemple avec quatre barres
assemblées en quadrilatère Quadrilatère formé par quatre barres de masses
proportionnelles à leur longueur: respectivement 1, 2, 3, 4 unités. La masse de chaque barre est concentrée en son
milieu. Le CG de m1 et m3 est situé sur la droite m1m3
avec une distance de 1/4 et de 3/4 de part et d'autre: M4 Le CG de m2 et m4 est situé sur la droite m2m4
avec une distance de 2/6 et de 4/6 de part et d'autre: M6. Le CG de M4 et M6 est situé sur la droite M2M6
avec une distance de 4/10 et de 6/10 de part et d'autre: CG10. Les quatre barres se comportent comme si leur
masse totale de 10 unités était concentrée en CG10. Voir Méthode
générale |
|
||
Merci à Philippe MOUTET pour
ses remarques
|
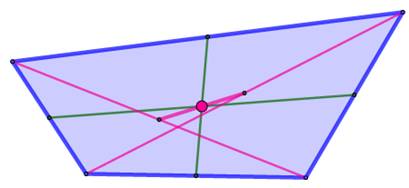
But Construire
le centre M d'un quadrilatère quelconque. Construction
1 (vert) 1.
Points
milieux des côtés. 2.
Rejoindre
deux à deux. 3.
Intersection
= point milieu du quadrilatère. Construction
2 (rose) 1. Diagonales. 2. Leur point milieu. 3. Segment joignant ces points milieux. 4. Le milieu de ce segment est le point milieu du
quadrilatère. Construction
minimale (figure du bas) 1. Points milieux de deux côtés opposés. 2. Segment les rejoignant. 3. Le milieu de ce segment est le point milieu du
quadrilatère. |
|
|
de gravité (de la surface) |
|
|
|
Construction
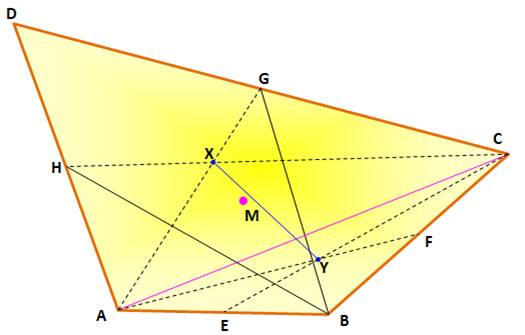
à partir des centres de gravité des quatre triangles: ABC, ACD, ABD et BCD. Centres
de gravité X et Y d'une paire de triangles (ABC et ACD). |
|
|
|
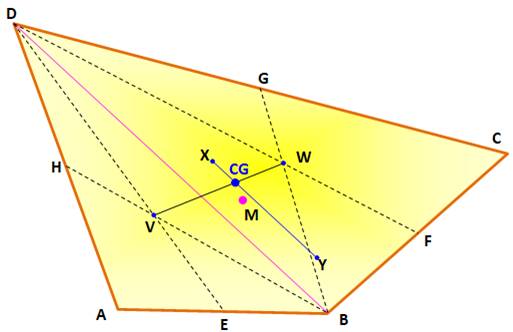
Centres
de gravité V et W de l'autre paire de triangles (ABD et BCD). Centre de
gravité CG du quadrilatère: point d'intersection des segments XY et VW. Note: en général, CG n'est pas le milieu M du
quadrilatère. |
|
|
|
Construction plus rapide
|
|
Voir Brève 55-1099
Référence A New and
Improved Method for Finding the Center of Gravity of a Quadrilateral – Behzad
Khorshidi
|
|
||
|
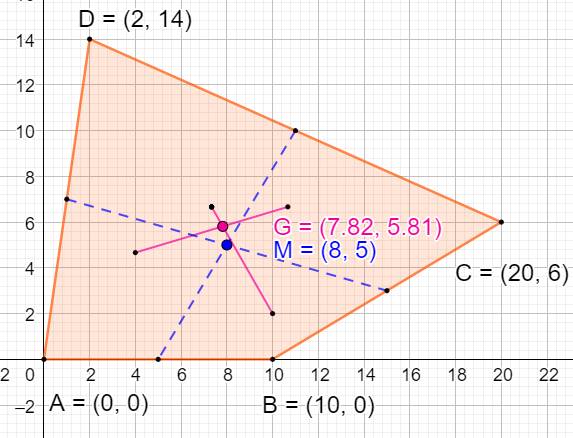
Rouge: G, centre de gravité Bleu: M, centre géométrique |
|
|
|
Centre géométrique de k points |
Exemple xM = (0 + 10 + 20 + 2) / 4 = 32 /
4 = 8 yM = (0 + 0 + 6 + 14) / 4 = 20 / 4 = 5 |
|
|
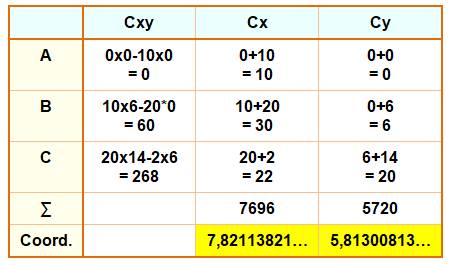
Centre de gravité de k points |
Avec A, l'aire du
quadrilatère.
Exemple X = [0, 10, 20, 2] et Y = [0, 0, 6, 14] A = 20x14 – 1/2 (10x6 + 2x14 + 18x8) = 280 – 116 = 164 Calcul des coordonnées
|
|
Retour Centre
de gravité de formes usuelles
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Site |
|
|
|
Cette page |
||
![]()