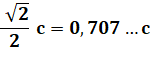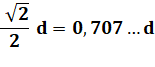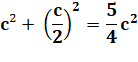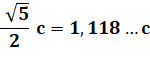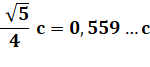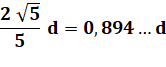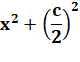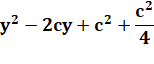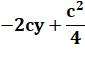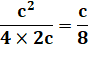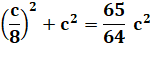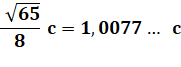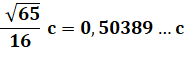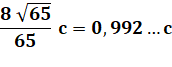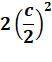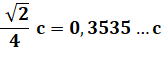|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Carré le plus grand couvert par k cercles identiques On dispose d'une dalle carrée. Quelle est le rayon
minimum des k disques nécessaires pour couvrir entièrement la dalle ? Ou inversement,
la taille du plus grand carré couvert par k disques ? On
sait: Problème
simple pour k jusqu'à 4. Pas évident pour k = 5. Optimum non prouvé pour k =
6. Prouvé pour 7. Une des références montre les solutions actuelles pour k
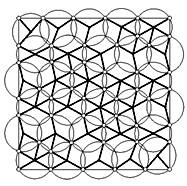
jusqu'à 30. Exemple
ave k = 30 => Anglais: How must the unit square be covered by k equal circles,
so that the radius r of the circles will be as small as possible? This
covering problem is the dual counterpart of the packing problem. |
|
|
||||||||||||||
|
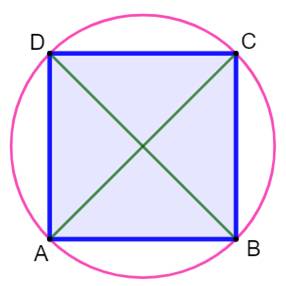
Problème Quel est le côté du plus grand carré recouvert
entièrement par un cercle de rayon r. Solution Il s'agit du carré
inscrit dans le cercle. Avec Pythagore:
|
|
|||||||||||||
|
|
||||||||||||||
|
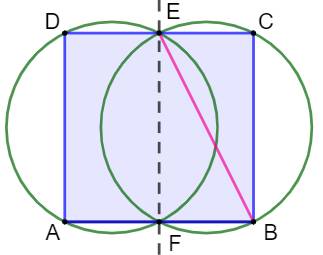
Problème Quel est le côté du plus grand carré recouvert
entièrement par deux cercles de rayon r. Solution Le cercle 1 passe par A et D. Le cercle 2 passe par B et C. Les deux cercles sont interchangeables. La figure
est symétrique. Les deux cercles passent par E et F, les milieux de AB et DC. Dans le triangle rectangle BCE inscrit dans le
cercle, BE est un diamètre.
|
Carré le plus grand couvert par
deux cercles identiques de rayon R. Son côté vaut 0,89…d.
|
|||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
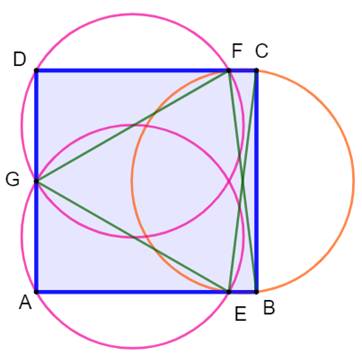
Problème Quel est le côté du plus grand carré recouvert
entièrement par trois cercles de rayon r ? Solution On retrouve deux cercles comme pour le cas
précédent. Ils ne recouvrent pas entièrement le carré, laissant le troisième
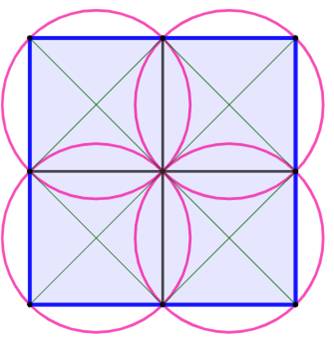
le faire. Les trois cercles forment un trèfle régulier à
trois pétales. On note AE = x, EB = y et d le diamètre des
cercles. Le point G est le milieu de AD. |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
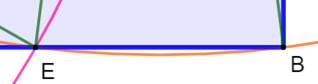
Notez que le troisième cercle couvre bien la
partie non couverte par les deux premiers. Le cercle n'est pas tangent, mais
il déborde et passe par les points E et B.
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||
|
Problème Quel est le côté du plus grand carré recouvert
entièrement par quatre cercles de rayon r ? Solution Chacun des quatre cercles est circonscrit à un
carré de côté c/2.
|
|
|||||||||||||
|
|
||
|
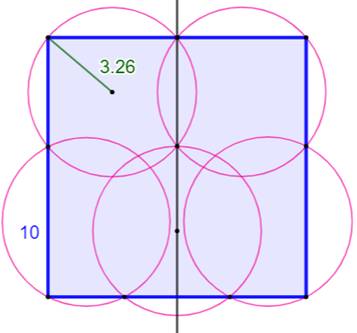
Problème Quel est le côté du plus grand carré recouvert
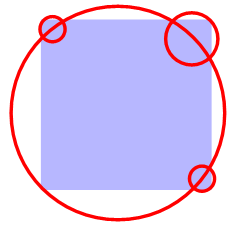
entièrement par cinq cercles de rayon r ? Construction de la solution Carré bleu de côté 10 cm; sa médiane verticale. Compas ouvert Cercle de
ce rayon (vert) passant par un sommet et le milieu du côté supérieur. Idem de
l'autre côté. Cercle centré sur la médiane passant par
l'intersection inférieure des deux cercles. Cercles latéraux-bas passant par un sommet et les
deux intersections de cercles. |
|
|
|
|
||
|
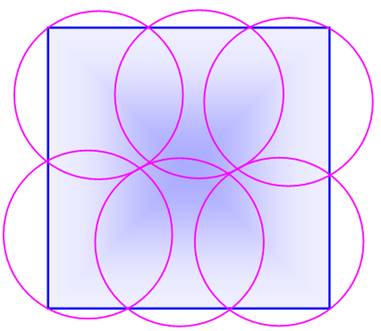
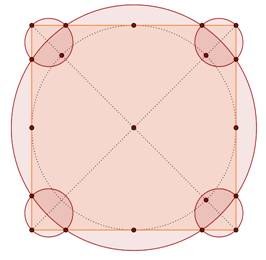
Problème Quel est le côté du plus grand carré recouvert
entièrement par six cercles de rayon r ? Solution La solution la plus optimale connue est celle-ci
avec: La construction n'est pas évidente. Elle résulte d'un calcul d'optimisation qui
délivre les coordonnées des points de construction. Résolution d'équations de
degré élevé. |
|
|
|
Ce tableau récapitule les valeurs du rayon r des k cercles couvrant le
carré unité. La suite du tableau et les figures correspondantes pour k = 1 à
30 se trouvent dans l'article en première référence. |
k et r
|
|
|
||
|
Certains
cherchent la taille maximale du carré sans se donner la contrainte du rayon
constant. Voici
deux exemples avec quatre et cinq cercles. Voir Les
références |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()