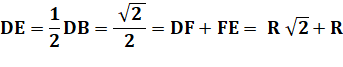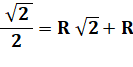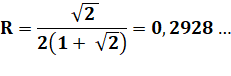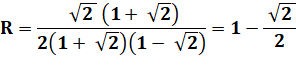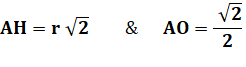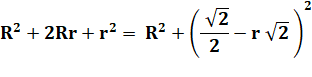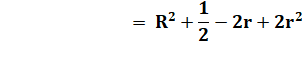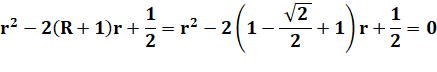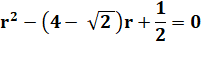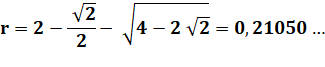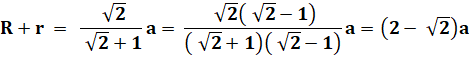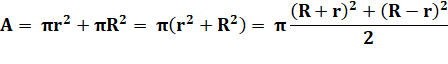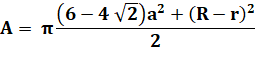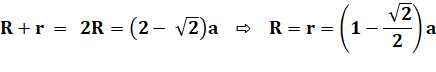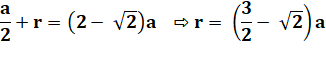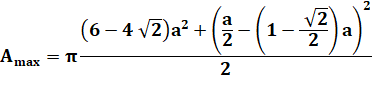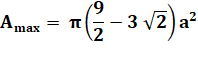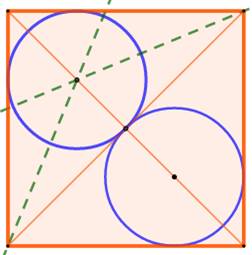
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
				Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Cercles inscrits dans le carré – Construction >>> Carré inscrit à deux cercles tangents – Construction >>> Deux cercles identiques dans un carré >>> Deux couples de cercles identiques dans un carré >>> Deux cercles dans un carré >>> Aires min et max

Les deux cercles dans le carré

Deux disques dans un carré

Comment construire deux cercles tangents dans le carré ?

Quelle est l'aire maximale pour ces deux cercles ?

Théorème du face à face (eyeball theorem)

Les deux cordes sous les arcs roses ont même longueur.

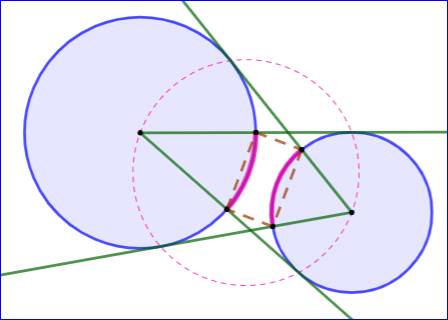
Voir Explications, théorème et preuve

Cercles inscrits dans le carré – Construction
Construction Un carré et ses diagonales. Tracer le cercle inscrit dans chacun des triangles rectangles. Méthode (commune à tous les triangles) Bissectrices des angles (vertes). Point de concours = centre du cercle. Construction du cercle bleu symétrique pour avoir deux cercles identiques inscrits dans le carré.

Carré inscrit à deux cercles tangents – Construction
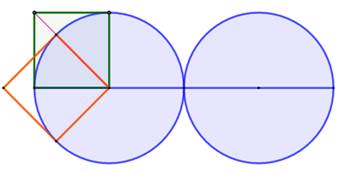
Construction Deux cercles tangents. Construire le carré circonscrit. Méthode Droite joignant les centres. Carré (vert) sur un rayon externe. Intersection cercle avec diagonale du carré. Carré (orange) porté par la diagonale. Perpendiculaire verticale au point de tangence des deux cercles (bleue). Droite portée par un côté du carré orange. Intersection avec la perpendiculaire bleue. Carré orange sorte d'extension du petit carré orange.

Deux cercles identiques dans un carré
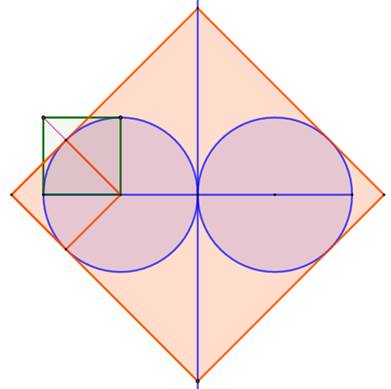
Question Un carré de côté AB = 1. Deux cercles de rayon R, tangents entre eux et tangents chacun aux côtés du carré. Quel est le rayon R ? Calcul

Voir Brève 52-1037

Deux couples de cercles identiques dans un carré
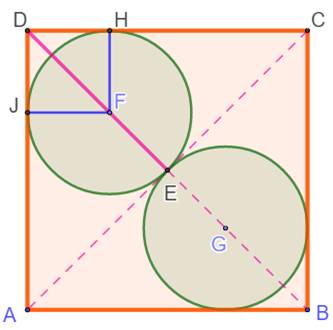
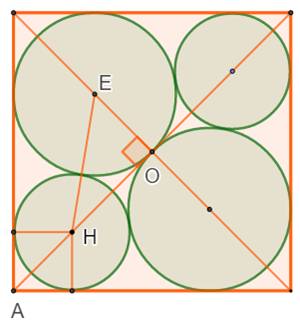
Question Le carré avec ses deux cercles tangents comme ci-dessus. Les deux petits cercles tangents sur l'autre diagonale. Quel est le rayon de ces cercles ? Calcul Dans le triangle rectangle OEH Or, avec les diagonales des carrés:
En reprenant la relation en carrés
Sous forme d'une équation en r
Racine compatible avec R > r	L'autre racine vaut: 2,37528…

Deux cercles de rayons différents dans un carré
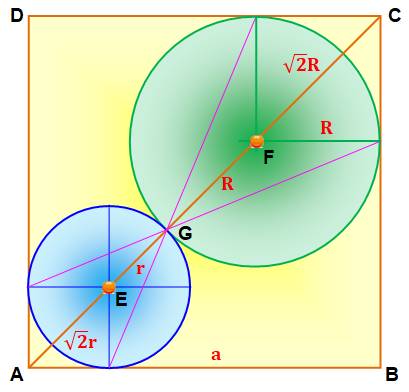
Un carré et deux cercles tangents entre eux et tangents aux côté du carré. Construction Dessiner le carré et sa diagonale. Dessiner le carré AE. Le point E est centre du petit cercle bleu. Ce cercle coupe AC en G. À partir des deux autres sommets du petit carré, tracez les droites passant par G et qui coupent le grand carré. À partir de ces nouveaux points d'intersection, dessinez le carré CF, puis le cercle de centre F. Les deux cercles sont homothétiques.

Aires min et max
Relation sur la diagonale AC => R + r = constante
Aire des cercles
Aire minimale Si R = r G est au centre du carré
Aire maximale Si R max = a / 2

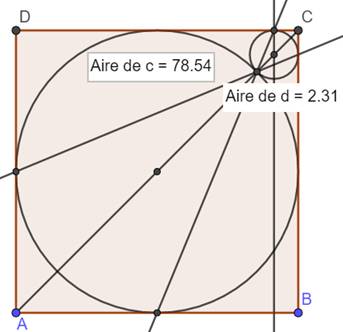
Configuration en aire maximale Vérification avec GeoGebra Calcul avec formule A = 10; R = 5; r = 0,8578 … S = 80,8518 … Pour GeoGebra: S = 78,54 + 2,31 = 80,85

Suite	Nombre d'or dans un carré et deux cercles Sangakus Rayon du cercle circonscrit Cercle inscrit Puissance d'un point par rapport à un cercle
Voir	Bissectrices Cercle – Index Cercles et triangles Cône	Diamètre Géométrie – Vocabulaire Périmètre Sphère
Sites	Empilement des cercles dans un carré – Wikipédia Deux disques dans un carré – Université de Lyon – Proposition de travaux Empilements dans le plan – Descartes et les Mathématiques Olympiades académiques 2008 – Descartes et les Mathématiques Olympiades académiques de première – 2002 – Académie de Poitiers – Propose plusieurs solutions 11) Sangakus : 2 cercles tangents dans un carré –Mathieu Morinière Sangaku – Cut The Knot – Réflexions et Index d'accès à de nombreux Sangakus
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/DeuxCerc.htm