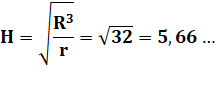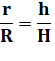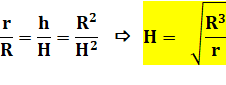|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
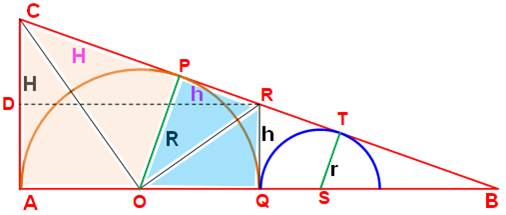
Deux cercles tangents inscrits dans un triangle isocèle Problème de construction géométrique
type Sangaku. Comment construire la figure et calculer
les proportions ? |
|
|
||
|
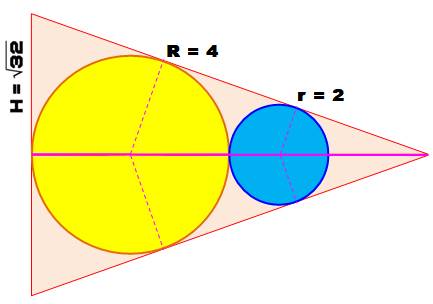
Un dessin de Sangaku Deux
cercles tangents sont dessinés avec R = 4 et r = 2. La demi
base du triangle isocèle vaut: |
|
|
|
|
||
|
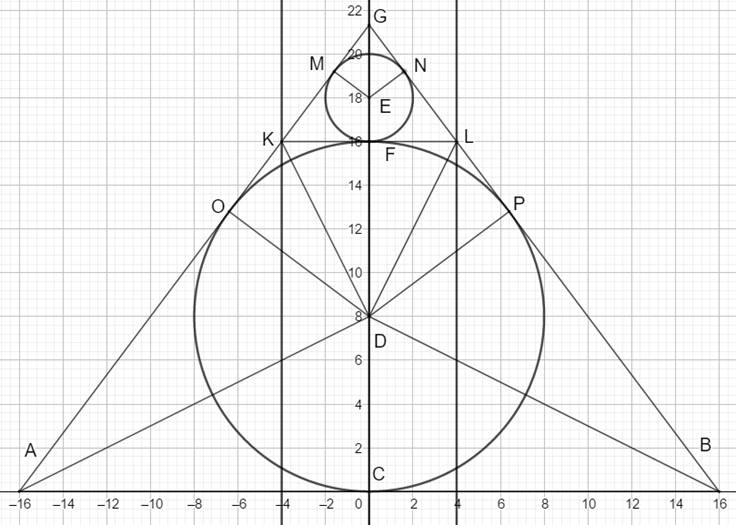
Construire la même figure avec ces
paramètres: r = 2, R = 8 et H = 16 (calculé) avec Geogebra (type règle graduée
et compas)
|
||
|
1. Tracer le segment AB = 2H = 2 x 16 2. Et son milieu C avec l'outil milieu 3. Perpendiculaire en C à AB 4. Matérialiser le point D (y = 8) 5. Dessiner le cercle (D, R = 8) |
6. Matérialiser le point E à y = 16 + 2 = 18 7. Dessiner le cercle (E, r = 2) 8. Tracer les tangentes AO et BP avec l'outil de tracé de la tangente. |
|
Voir Outils informatiques
/ Construction
règle et compas
|
|
|||
|
Proportionnalité dans les
triangles semblables de sommet B:
Rappel: les
rayons aux points de tangence (A, Q, P, T) forment des angles droits. |
|
||
|
Les points C et r sont des
points de convergence de tangentes au cercle. |
H = CA = CP h = RP = RQ |
||
|
Triangle
CDR et Pythagore. |
DR = 2R CD = H – h CR = H + h (H + h)² = (2R)² + (H
– h)² H² + 2Hh + h² = 4R² +
H² – 2Hh + h² R² = Hh |
||
|
En
rapprochant les deux relations: |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()