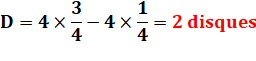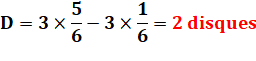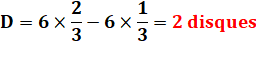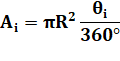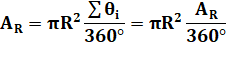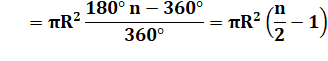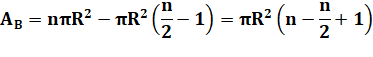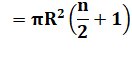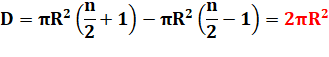|
Édition du: 16/09/2023 |
|
INDEX |
CERCLES |
||
|
Trois cercles – Construction |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
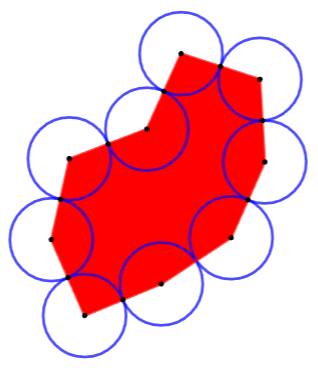
Chapelet de cercles
Une série
de cercles de même rayon et tangents deux à deux. Surprise
ou paradoxe: la différence d'aire entre les secteurs externes (bleus) et les
secteurs internes (rouges) est constante et égale à 2π quel que soit le polygone. On retrouve
une propriété semblable avec le paradoxe de la corde tendues
autour d'un cercle. |
||
|
|
Sommaire de cette page >>> Cas de polygones simples >>> Calcul d'angles >>> Cas de polygones quelconques >>> Calculs express |
Débutants Glossaire |
|
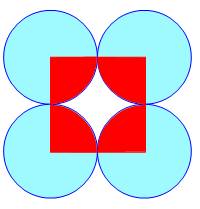
Carré et cercles À
chaque sommet d'un carré, on place un cercle centré sur le sommet et de rayon
moitié du côté du carré. Les cercles sont donc tangents deux à deux. Quelle
est la différence d'aire entre la zone bleue et la zone rouge ? Réponse Cette
différence se lit sur la figure: |
|
|
|
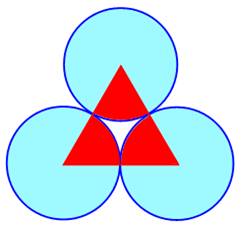
Triangle équilatéral et cercles À
chaque sommet du triangle, on place un cercle centré sur le sommet et de
rayon moitié du côté du triangle. Les cercles sont donc tangents deux à deux. Quelle
est la différence d'aire entre la zone bleue et la zone rouge ? Réponse Cette
différence se lit sur la figure: |
|
|
|
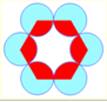
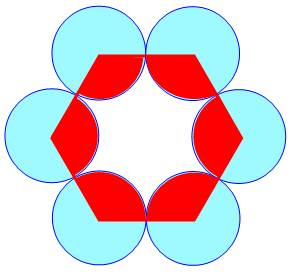
Hexagone et cercles À
chaque sommet, on place un cercle centré sur le sommet et de rayon moitié du
côté de l'hexagone. Les cercles sont donc tangents deux à deux. Quelle
est la différence d'aire entre la zone bleue et la zone rouge ? Réponse Cette
différence se lit sur la figure: |
|
|
|
Observation Quelle
que soit la figure, la différence d'aire est égale à celle de deux disques. |
Est-ce
généralisable à tout polygone ? Régulier
ou irrégulier ? Convexe
et concave ? Réponse:
oui ! |
|
Voir Brève
53-1042
|
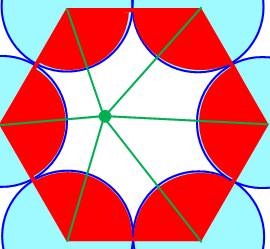
Dans l'hexagone Prenons
un point quelconque et traçons tous les segments joignant les sommets. On
forme ainsi six triangles dont la somme des angles de chacun est 180°, soit un
total de 6 × 180°. Parmi
eux, l'angle au centre fait 360°. Les
autres angles, ceux de la zone rouge, comptent pour: AR = 6 ×
180° – 360°. Généralisation Un
polygone quelconque à n côtés conduira à la formation de n triangles. Le même
raisonnement que ci-dessus s'applique et donne la formule pour les angles
rouges: |
|
|
|
Aire et angles L'aire
d'un secteur rouge est proportionnelle à l'angle du secteur. L'aire
de toutes les zones rouges devient: L'aire
de toutes les zones bleues, par différence: Différence
entre zone bleue et zone rouge: |
|
|
|
Somme des
angles de la zone rouge: 180n – 360 Somme des
angles de la zone bleue: 180n + 360 Différence
d'angles (bleue – rouge): 2 ×
360 |
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |