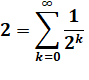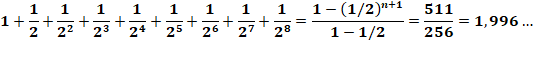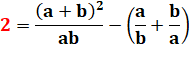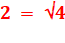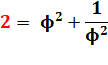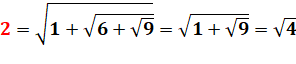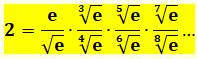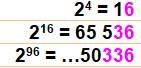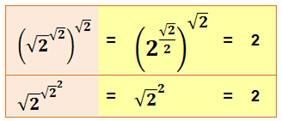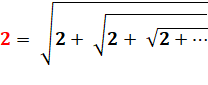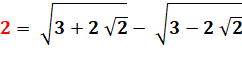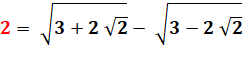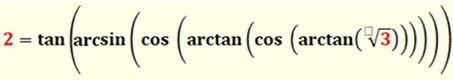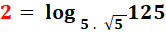Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 20/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	-0-	-1-		-2-	-3-		-4-	-5-	-6-	-7-	-8-	-9-

Nombre 2	Culture 2	Maths 2	De 2 à 2,7	Expression en 2
Débutant 2	Culture 2 suite	Maths 2 suite	De 2,7 à 3	Proverbes avec 2
Quiz 2	Quantité 2	Binaire	Sciences 2	Dualité (yin-yang)
Horloge maths	Pluriels détournés	Bissection	Puissance de 2	Multi-puissance 2
		Duplication	Max avec trois 2

Deux

Two

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	10
Bases	/
Romain	II

Suite

Caractérisation du nombre

Bell

Catalan

Chanceux d'Euler

Chanceux d'Ulam

Curzon

Dedekind

Déficient

Dihédral

Eisenstein

Factoriel premier (le seul)

Factorielle double

Factorion (2! = 2)

Faiblement totient

Fibonacci (3^e)

Glissant

Hamilton

Heegner

Idéal

Idonéal

Intouchable

Jordan-Polya

Kynea

Lucas premier (rang)

Markov

Mertens nul

Motzkin premier

Padovan

Pair Seul nombre premier pair. Noté E pour even en anglais.

Pell

Perrin (2 fois)

Pratique

Premier (le plus petit et le seul pair)

Premier bon

Premier de Bertrand

Premier de Chen

Premier de Pierpont

Premier de Ramanujan

Premier de Sophie Germain

Premier de Stern

Premier de Woodall

Premier factoriel (2 = 1! + 1)

Premier horloge

Premier inévitable (ou minimal)

Premier minimal

Premier primorielle (2 = 1# + 1)

Primeval

Primorielle

Pronique Intouchable

Queneau

Refactorisable ou tau

Schröder

Semi-parfait primaire

Smarandache-Wellin

Sous -factorielle

Stirling 1

Sylvester

Tangent

Thabit

Totient (Phi)

Tribonacci

Woodall (2 × 2² – 1 = 7 est premier)

Wieferich (paire avec 1093)

Zuckerman

Géométrique

Gâteau (cake)

Tarte ou pizza

2-pentagonal (1^er)

Deux points
délimitent un segment.

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

N'oubliez pas! Si vous on vous demande de souffler dans le ballon pour l'alcotest, enlevez vos lunettes… Ça fera toujours deux verres en moins !

Two is the oddest prime. Deux est le nombre premier le plus étrange.

(Jeu de mot avec "odd" qui veut dire à la fois étrange et impair).

Voir Pensées & humour / Expressions en deux

PROPRIÉTÉS MATHÉMATIQUES générales

Général	Dualité Pair / Impair; Masculin / Féminin; Vrai / Faux; Yin/ Yang …		Dualité Parité
Jeux	2 + 2 = poisson, sujet d'une énigme.		>>>
Nombre	0, 2, 4, 6 … 2n Nombres pairs: divisible par 2.		>>>
	Second et deuxième Le second est le deuxième d'une liste de deux. Premier, second. Premier, deuxième, troisième …		>>>
	Deux diviseurs Un nombre ayant strictement deux diviseurs est un nombre semi-premier.		>>>
	2 =		>>>
	Base 2 Numération binaire avec les seuls chiffres: 0 et 1.		>>>
Arithmétique	Vous savez doubler les nombres, alors vous savez effectuer n'importe quelle multiplication!		>>>
	2 + 2 = 2 x 2 Seul nombre à faire la même chose en addition et multiplication (hors 0).		>>>
	n + n = 2 n n x n = n² Double et carré.		>>>
Suite	1 et 2: nombres de la suite de Kolakoski.		>>>
Logique	Une proposition logique est soit vrai ou fausse: principe du tiers exclu.
Test en Informatique	Un nombre n est pair si n mod 2 = 0 Un nombre n est pair si, en binaire, son dernier bit est 0.		>>>

Théorie des nombres	x² + y² = z² Il y a une infinité de triplets de Pythagore. 3² + 4² = 5² est le plus petit et le plus célèbre.	>>>
	E = P + P' Tout nombre pair (E = even) est la somme de deux nombres premiers (P et P'). Conjecture de Golbach.	>>>
	n < p < 2n Théorème de Tchebychev (postulat de Bertrand): il existe toujours un nombre premier entre n et 2n.	>>>
	E = p + q Tout entier pair (>2) est la somme de deux nombres premiers. Conjecture forte de Goldbach.	>>>
Algèbre	ax² + bx + c = 0 Équation du deuxième degré.	>>>
	Nombres complexes: algèbre à 2 dimensions.	>>>
Géométrie	2 points Par deux points distincts passe une droite et une seule.	>>>
	2 = S – A + F Relation d'Euler entre sommets, arêtes et faces pour tout polyèdre.	>>>
	2 points immobiles Pour un anneau qui se déforme uniformément.	>>>
	L'angle au centre = 2 x angle inscrit	>>>
	r = 2 rayon du cercle inscrit dans le triangle de Pythagore (5, 12, 13)	>>>

PROPRIÉTÉS MATHÉMATIQUES détaillées

Général

2	Plus petit nombre premier, seul a être pair. Seul premier tel que 1 / (p – 1 ) est entier. Plus petite base de numération – Système binaire. Plus petit nombre chanceux. Premier de Sophie Germain (2 et 2 x 2 + 1 = 5 sont premiers. Départ d'une séquence de Sophie Germain: 2, 5, 11, 23, 47). Premier de Woodall d'ordre 3. Aussi, plusieurs fois générateur de nombres de Woodall d'ordre n. Nombre Intouchable, jamais somme des diviseurs d'un nombre.
2! = 2 2# = 2 3! = 2	Seule factorielle égale à son nombre et seule première. Seule primorielle égale à son nombre et seule première. Sous factorielle de 3.
2, 3, 6	Triplet harmonique, le plus petit: 1/2 – 1/3 = 1/3 – 1/6 = 1/6

Addition

2 = 1 + 1 = 2	Quantité de partitions du nombre 2 = 2.
2 + 2 = 2 x 2	Seul nombre entier à faire la même chose en addition et multiplication (hors 0). Voir le cas général.
2 + 2 = 2 x 2 = 2² 4 / 2 = 4 – 2 2! = 2	Quelques formes amusantes (anagrammes numériques).
2 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 +... = 1 + 0,5 + 0,25 + 0,125 + 0,0625 +...	Série égale à 2. Progression géométrique de raison 1/2 Voir Achille et la tortue
Exemple de calcul de la série géométrique avec n = 8
	Somme infinie des inverses des nombres triangulaires.

	Expression des factorielles avec somme de puissances.
210 = 102 1,999…10 = 1,111…2 = (1 + 0,1 + 0,001 + 0,0001 + …)2	En binaire. Écriture avec nombre périodique du nombre 2 et sa valeur binaire. Somme de décimaux binaires qui rappelle la somme des inverses des puissances de 2.
2 = 1/13 + 1/19 +...+ 1/990 + 1/992	Fractions égyptiennes.
10 = 3 + 7 = 5 + 5	Tout nombre pair est la somme de deux nombres premiers. Conjecture de Goldbach.

Table de multiplication du 2

Voir Table complète

Multiplication

2 = 1 x 2 2 = 1 x 3^1 – 1 2 = 2! 2 = !3 = 3! (1 – 1/1! + 1/2! – 1/3! ) 2! + 1 = 3	Pronique. Premier de Woodall d'ordre 3. Factorielle 2. Sous-factorielle 3. Factorielle plus 1 donne un nombre premier.
Multiplication en divisant par 2	Multiplication égyptienne.
2 = (t + 1) (t – 1)²	Avec la constante (t) de tribonacci.

Division

2n est divisible par 2	Tous les nombres pairs sont divisibles par deux.
	Motif général dont le résultat est la division des termes centraux.
n^2 n est divisible par 2	Comme de nombreuses autres formes.
	Identité remarquable revisitée.
2 et 5 = 2 x 2 + 1 2, 5, 11, 23, 47	Deux premiers de Sophie Germain Séquence de 5 nombres premiers de Sophie Germain.
0, 2, 4, 6 ou 8 Nombres pairs	Un nombre avec ces unités est divisible par 2. Il y a 499 nombres inférieurs à 1000 divisibles par 2 dont 374 avec des chiffres tous différents.
1/2 = 0,5	N Pair N/2 = nombre entier. N Impair N/2 = nombre avec une décimale égale à 5.

Avec des puissances

Voir Puissance / Racine

	Racine carrée de 4.
	Somme nombre d'or et son inverse au carré.
			Curiosité impliquée dans une démonstration de géométrie.
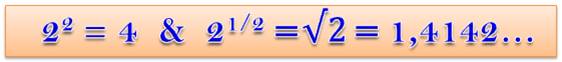
2 =			Voir réduction des racines emboitées.
		Expression avec triple racine carrée.
2 = 2^2 – 2^1	Différence de puissances d'un même nombre.
2 = 3^3 – 5^2	Différence entre puissances (seule différence égale à 2 jusqu'à un million et sans doute au-delà)
2^a – 3^b	Il existe 37 nombre inférieurs à 100 atteints par cette formule.
2 x 2^2 – 1 = 7	Nombre de Woodal.
2 et 1093	Paire de Wieferich.
2 = (n – 1)² – 2n² + (n + 1)² Ex: 5² + 3² = 2 x 4² + 2	La différence d'ordre 2 entre carrés de nombres successifs est égale à 2.
2 = 1 214 928^3 + 34 80 205^3 – 35 28 875^3	Plus petite forme de cette nature pour 2. Voir 12 2 = 1 793 294 529 295 306 752 + 42 151 640 334 749 615 125 - 43 944 934 864 044 921 875
(a + b)² = a² + 2ab + b²	Identité remarquable: double produit et deux carrés. Voir Nombre 169
	§ Le plus petit nombre premier de cette forme.
	§ Dans cette égalité se cache la série harmonique.

2 = 7^3 – 6^3 – 5^3 = 343 – 216 – 125 = 49^3 – 47^3 – 24^3 = 117 649 – 103 823 – 13 824	Somme de trois cubes. Voir La formulation générale.
2 = 7^3 – 6^3 – 5^3(n+1)^3 – n^3 – (n–1)^3 = –n^3 + 6n^2 + 2 (n+2)^3 – n^3 – (n–2)^3 = –n^3 + 12n^2 + 16 16 = 14^3 – 12^3 – 10^3	Seul tel motif donnant 2. En effet, la somme algébrique s'annule pour n = 6. Avec un intervalle de 2, la somme algébrique minimale est atteinte pour 12 et vaut 16.

Puissances et racines de 2

2, 3, 5, 8 a = 5.8 – 2.3 = 34 ; b = 2.3.5 = 30; c =2.8 = 16 a² = b² + c² = 1 156	Quatre nombres de Fibonacci qui forment un triplet de Pythagore. Vrai pour tout quadruplet de nombres successifs de Fibonacci.
2² = 4 = 2^1 + 2^1 2^6 = 64	Seule solution de n^x + n^y = n^z Mnémotechnique avec 6 & 6 Voir Puissance de 2 / Premiers en 2^n± 1
2^3 = 8 2^9 = 512 et 5 + 1 + 2 = 8	Mêmes sommes des chiffres des puissances.
2^2 – 1 = 3 2^4 – 1 = 15 2^6 – 1 = 63 2^8 – 1 = 255 …	Toutes les puissances paires de 2 moins 1, sont divisibles par 3.
	§ Les trois plus petites puissances de 2 se terminant avec des 3 et des 6. Voir Brève 715
2^9 = 7^3 + 13^2 = 512	Puissance = somme de puissances.
	Un des trois nombres pannumériques puissants Tous les chiffres de 0 à 9, une seule fois.

(2² + 3²)² = 8^3 – 7^3 = 169 = 13²		Avec nombres successifs des deux côtés.
2²² = 4 194 304 2²^²² = 2 ^4 194 304 = 2,06506354… × 10^1 262 611		Plus grand nombre avec trois 2 et plus grand nombre avec quatre 2. Voir Échecs / Tour de Brama ou de Hanoi
2^3 = 8 22^3 = 10 648 222^3 = 10 941 048 2222^3 = 10 970 645 048 22222^3 = 10 973 607 685 048 222222^3 = 10 973 903 978 085 048			Tous ces cubes de nombres 2-repdigits sont sans le chiffre 2. Pas au-delà.
2^n = (1 +…+ 1)n		Somme des coefficients de la ligne n du triangle de Pascal.
2^n éléments	Soit un ensemble E de n éléments. L'ensemble constitué des parties de E comporte 2^néléments. Exemple avec un ensemble de trois éléments
	Hypothèse du continu: le cardinal des nombres réels est égal au cardinal strictement supérieur à aleph zéro.

1 / 49 = 0,020408163265...	Puissance de deux successives (au début …) Voir Nombre 49
2 = 0,5 / (1 – 0,5) = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 +... = 1 + 0,5 + 0,25 + 0,125 + 0,0625 +...	Série des inverses des puissances d'un nombre.
	Irrationnels qui produisent du rationnel ! Voir Puissances de racine de 2
	Racine continue / Équation du 2^e degré.
Une des quatre valeurs possibles. Les trois autres impliquant des racines de nombres négatifs. Comme: la racine de 4 est 2 ou -2. Cependant l'utilisation du symbole indique que l'on s'intéresse uniquement à la racine positive.

Trigonométrie

	Une des rares valeurs entières de la sécante (inverse du cosinus). Vaut -1 pour Pi; Vaut racine de 2 pour Pi/4 ou 2/3 de racine de 3 pour Pi/6.
	Propriété des angles d'un triangle quelconque.
		Nombre trigonométrique.

Logarithme / Complexes

2 = log a a²	Propriété. Exemple curieux. Voir Calcul avec les logarithmes
2 = (1 + i) (1 – i) = 1 – ( –1) 2 = (1 + i)² . i^– 1 = (1 + 2i – 1) / i	Identité remarquable avec i. Voir Complexe

Équations

ax² + bx + c = 0	Équation du second degré.
x^n + y^n = z^n x^2 + y^2 = z^2	Le nombre 2 est le plus grand entier tel que cette équation possède des solutions entières. Voir Triplets de Pythagore / Théorème de Fermat-Wiles
n^x + n^y = n^z 2^1 + 2^1 = 2^2	Seule solution entière de cette équation. Voir Équations diophantiennes
x ^y = y ^x 2 ^4 = 4 ^2	Seule solution en nombres entiers.
n^x – m^y = 2 3^3 – 5^2 = 27 – 25 = 2	Le nombre 2 est une des rares solutions de cette équation. La seule ?
	Seule solution entière.

Jeux et curiosités

	12 divisions pannumériques avec quotient égal à 2.
	Jeu du quatre 4.

SUITE >>>

Décimales

Voir pages dédiées >>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]	Repdigit (Brésilien)
2, [1, 0]	/

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombres – Glossaire Nombre 2 en maths – Suite Suite en 2,… (décimales)
Voir	Carrés Chemin d'Euler Dualité Exponentielle Pair
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/DeuxP11.htm