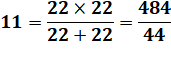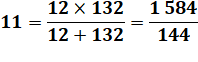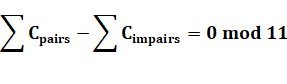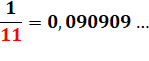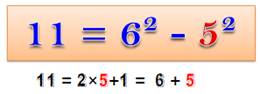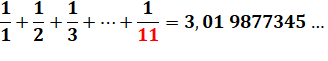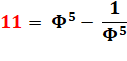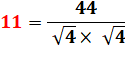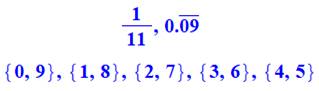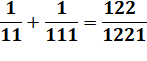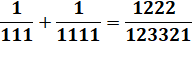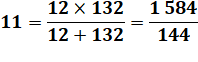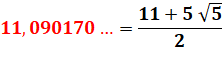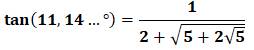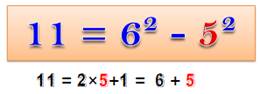nombre - onze en maths

Édition du: 03/11/2024

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 11	Culture 11	Maths 11	Expressions en 11	Nombre 11
Curiosités 11	Culture (suite)	Multiplication 11	Sciences 11	Curiosités 11
Horloge maths	Repunit 11	Divisibilité par 11	Puissance 11	Horloge maths

Onze

Eleven

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1011
Bases	102₃ 11₁₀
Romain	X

Suite

Caractérisation du nombre

Bon

Chanceux d'Euler

Déficient

Dichotomique premier

Dihédral

Euler – Permutations

Glissant

Hamilton

Heegner (-11)

Impair

Jacobsthal (5^e)

Lucas (5^e)

Lucas premier (rang)

Partition

Premier (5^e)

Premier bon

Premier de Chen

Premier de Sophie Germain

Premier fort

Premier horloge

Premier inévitable (ou minimal)

Premier jumeau avec 13

Premier minimal

Premier pointé

Premier sûr

Premier supersingulier

Premier unique

Queneau

Stirling 1

Strictement non palindrome

Thabit

Trivialement permutable

Ulam

Zuckerman

Nombres géométriques

Décagonal centré (2^e)

Dihédral

Hendécagonal

Palindrome

Repunit (le plus petit)

Strobogrammatique

Tétradique

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Nombres hendécagonaux

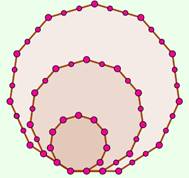
1, 11, 30, 58, …

Nombre Tarte ou pizza

11 parts en 4 coupes

Rappel Propriétés générales >>>

Devinette

Comment dit-on: "sept et trois font t'onze ou sept et trois font z'onze ? "

Colle que mes grands cousins Jean et Jeanne, tous deux instituteurs, me posèrent lorsque j'avais huit ans. Je n'ai pas trouvé la bonne réponse et m'en veux encore, soixante ans plus tard. Preuve qu'il y a des souvenirs d'enfance très tenaces.

Sept et trois font dix, bien sûr!

Voir Pensées & humour / Jeux et énigmes

Magie du nombre 11

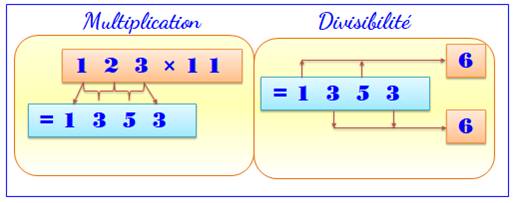
Voir Calculs / Multiplication par 11 / Divisibilité par 11

Numération – Chiffres – Dénombrement

11	Repunit ou nombre uniforme en 1. Seul palindrome premier à nombre pair de chiffres.
11	N'est repdigit dans aucune base. Il n'est pas brésilien.
11 + 1 + 1 = 13	Nombre + chiffres = premier suivant.
11³ = 1 331 11 = (1x3x3x1) + (1+1)				Nombre égal au produit des chiffres du cube + somme des chiffres.
11₁₀ = 102₃ = 9 + 0 + 2				Le plus petit pannumérique en base 3.
111 = 11 + 100				Seul nombre de la forme X + y = X + 100.
11 = 2 + 3 + 6 & 1/2 + 1/3 + 1/ 6 = 1				Nombre bon; le plus grand avec 3 fractions.
11 chiffres dans 1212…21				Le deuxième nombre premier ondulant en 12. Le premier a 7 chiffres et le suivant 43.
(1 + 1) / 2 = 1 x 1				Curiosité avec deux chiffres 1.
11² = 121 (1 + 1)² = 1 + 2 + 1			Le carré de la somme des chiffres est égal à la somme des chiffres du carré. Liste: 0, 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 30, 31, 100, 101, …
11 = ½ 4 x 5 + 1		Nombre tarte: quantité maximale de parts de tarte obtenue en la coupant avec 4 coups de couteau.

Addition – Partition

p(11) = 56	Quantité de partitions du nombre.
11 = 1 + 2 + 3 + 5	Partition unique avec quatre chiffres différents.
11 partitions	Partitions du nombre 6.

Multiplication – Division

Table de multiplication du 11

Voir Table complète

01234 x 11 = 13 574 01234 12340 13574	Multiplication rapide par 11: Pour chaque chiffre, lui ajouter celui de droite. Tenir compte des retenues. Mettre des 0 sur les bords.
11 x N = NN	Tous les multiples à un chiffre de 11 sont des repdigits à 2 chiffres. Ex: 11 x 7 = 77.
N x 11 = M *r N* x 11 = *r M*	Produits réversibles par 11. Exemple: 123 x 11 = 1 353 321 x 11 = 3 531 Voir Suite
11 x 101 x 10001 = 11 111 111	Produit en repunit.
11, 2, 4, 16, 42, 48, 384, 1440, 0	Record d'itérations somme x produit des chiffres.
11 = n.m / (n + m)	Cette divisibilité existe pour deux couples de nombres seulement.
	Nombre glissant.
2 × 3 × 5 × 7 × 11 – 1 premier	Primorielle – 1 première.

Motif itératif produisant les chiffres successifs

Voir Repunit / Pépites

Les divisions par 11 sont périodiques d'ordre 2

Pour diviser un nombre par 11, multipliez le numérateur par 9 …

Ex: 3/11 => 3 × 9 = 27 => 0,272727…

La division par 11 des nombres de 1 à 10 produit cinq types de suites périodiques à deux chiffres et leur permutation:

{09, 18, 27, 36, 45}

Le nombre premier 11 est le plus petit produisant des fractions d'ordre 5.

Avec d'autres numérateurs, on retrouve les mêmes décimales précédées d'une partie fixe:

12/11 = 1,090909…

13/11 = 1,181818…

100/11 = 9,090909…

1234/11 = 112,181818…

Voir Brève 54-1071

		Divisibilité par 11 & Preuve par 11. Ex: 135 795 => (1+5+9) – (3+7+5) = 0 Ce nombre est divisible par 11. Il est souvent plus rapide de faire le calcul au fil des chiffres: 1 – 3 = –2; + 5 = 3; – 7 = –4; + 9 = 5; –5 = 0
10ⁿ – 9ⁿ + 8ⁿ – 7ⁿ + 6ⁿ – 5ⁿ + 4ⁿ – 3ⁿ + 2ⁿ – 1ⁿ	Divisible par 11 pour les puissances paires.
xy + yx est divisible par 11	Un nombre de deux chiffres ajouté son retourné est divisible par 11.
xyyx est divisible par 11	Forme palindrome. voir Théorème.
abcabc est divisible par 11	voir Nombres répétés.

11 => 11, 13, 17, 19, 31, 41, 61, 71	Le nombre 11 engendre huit nombres premiers en modifiant un de ses deux chiffres. Plus petit cas; le nombre 13 en produit 10.
1, 2, 3, 5, 11, 31, 127, 709, 5381, 52711, 648391, …	Suite de premiers telle que le suivant est le nombre premier du rang du précédent. Ainsi 11 est le 5^e nombre premier. OEIS A007097
	Seuls les nombres 6 et 11 ont une somme de diviseurs égale à 12. Multiples de 5 plus 1. Objet d'une énigme.
	Le plus petit nombre tel que son totient (phi) atteint 2 après trois itérations.
1/11 = 0,09 09 09 … 2/11 = 0,18 18 18 … 3/11 = 0,27 27 27 …	Décimales répétitives en multiples de 9. Le seul nombre de période 2. 11 est un nombre premier unique.
	Division par 11 et nombres périodiques. Voir pourquoi les divisions par 11 engendrent des nombres périodiques.
11/12 = 1/2 + 1/4 + 1/6 = 6/12 + 3/12 + 2/12		Voir Partage des chevaux.

Premier

11 est repunit premier	Le plus petit premier à deux chiffres. On ne connaît que cinq repunits premiers avec 2, 19, 23, 317 et 1031 fois le chiffre 1.
11, 13, 17	Triplet de premiers pointés; on passe au suivant en ajoutant les chiffres du précédent. Le plus petit triplet.
11, 13, 17, 19	Premier quadruplet de premiers dans une dizaine. Le suivant: 101, 103, 107, 109. Outre: 2, 3, 5, 7. Il y en a une infinité.
11 et 13 sont jumeaux	Séquence typique de jumeaux et de cousins: 5, 7, 11, 13, 17, 19
[2, 5], [4, 11], [6, 29], [8, 97],	Plus petits nombres premiers avec écart croissant par rapport au premier précédent.
10 = 2.5 130 = 2.5.13 11 premier 131 premier 12 = 2².3 132 = 2².3.11	Plus petit nombre premier 2-sandwich: les deux nombres voisins ont tous 2 deux facteurs. Notez la ressemblance avec 131, le 3-sandwich.
11 & 2 x 11 + 1 = 23 sont premiers 5 & 2 x 5 + 1 = 11 sont premiers	Nombre premier de Sophie Germain. Premier sûr.
11, 13, 17, 23 … 101	Séquence de 10 nombres premiers en progression: 2, 4, 6 …
11 > (7 + 13) / 2	Premier fort: supérieur à la moyenne arithmétique de ses voisins. C'est le plus petit.
11, 1361, 136 361, 13 636 361, 1 363 636 361 et 136 363 636 361	Tous premiers par insertion du nombre 36.

Avec des puissances

	Tout nombre impair est la somme de deux nombres consécutifs et la différence des carrés de ces nombres consécutifs: 11 = 6 + 5 = 6² – 5² 111 = 56 + 55 = 56² – 55² 1111 = 556 + 555 = 556² – 555² Le motif semble sympathique mais n'a rien de magique.
11 = 1² + 1² + 3² = 1³ + 1³ + 1³ + 2³		Seule somme de puissances de 2 à 5 avec deux à cinq termes.
11 = 5 (2² – 2) + 1		Nombre décagonal centré.
11 = 6 + 5 = 6² – 5²		Différence de deux carrés de nombres consécutifs. Motif valable pour tout nombre impair.
11 = 2¹ + 3² = 2³ + 3¹ 35 = 2³ + 3³ = 2⁵ + 3¹ 259 = 2⁸ + 3¹ = 2⁴ + 3⁵		Deux fois en 2^a + 3^b. Sans les trois nombres de cette forme avec deux présentations.
6² – 5² = 11 6⁴ – 5⁴ = 671 = 11 x 61		Motif divisible par 11 pour les puissances paires.
11 = 6² – 5² = 36 – 25 = 6 + 5		Possibilités de tirer au moins un 6 en lançant 2 dés.
		Différence entre puissances.

Puissances du nombre

Puissances palindromiques des repunits

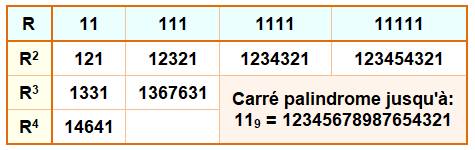
Voir Palindrome / Repunit

= 3,3166247903…

Angles que l'on retrouve dans l'hendécagone.

etc.

Tous les repunits avec 2k fois le "1" ont une racine carrée qui commence avec 2k fois le "3".

Le produit de quatre nombres consécutifs plus 1 est un carré.

11² x 2² = 22²

121 x (1 + 2 + 1) = 22²

Deux écritures pour le même résultat remarquable. Voir Généralisation / Brève 444

11² = 121 => 1+2+1= 4 = 2²

11³ = 1 331 => 1+3+3+1= 8 = 2³

11⁴ = 14 641 => 1+4+6+4+1= 16 = 2⁴

Nombre dont la somme des chiffres du carré est un carré, celle du cube est un cube et celle du bicarré un bicarré. Tous en puissance de 2.

11 = 11

11² = 121 = (12 – 1)²

11³ = 1331 = (13 – 3 + 1)

11⁴ = 14641 = (14 – 6 + 4 – 1)⁴

Le triangle de Pascal se retrouve dans les puissances de 11 jusqu'à la quatrième ligne.

Palindrome dont le carré est palindrome. Palindromes pour ces puissances.

Les suivantes ne sont pas palindromes.

11² = 121

34² = 1156

Plus petit carré comportant deux "1".
Suivants: 34, 39, 41, 46, 101, …

11² = 23 + 42 + 56 = 65 + 24 + 32

22⁴ = 234 256

& 2+3+4+2+5+6 = 22

Coquetterie miroir avec les chiffres.

Le nombre 22 est NESCHIP.

Carrés comportant de plus en plus de "1"

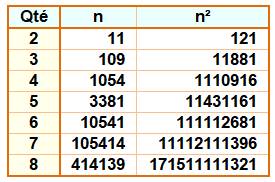
Voir Tableau pour la répétition des autres chiffres dans le carré

11² = 2² + 6² + 9²		Seule somme de trois carrés distincts.
11² = 5! + 1		Problème de Brocard en 4.
11² = 56 + 65 = 121 = 23 + 42 + 56 = 65 + 24 + 32		Palindrome et somme palindrome. Somme palindrome.
11² = 3⁰ + 3¹ + 3² + 3³ + 3⁴		Curiosité.
11² = (3 – 2)! + (3 + 2)!		Seul motif de cette sorte.
11² – 5³ = –4 = 121 – 125 11 = 3³ – 4² = 27 – 16 11 = 15³ – 58² = 3 375 – 3 364		Équation de Bachet pour k = 4. L'une des deux solutions avec 2² – 2³ = –4. Différence entre un cube et un carré. Deux cas d'équations de Bachet avec k = 11.
		Un des trois tels motifs.
11³ = 1331 11³ = 10 x 11 x 12 + 11 = 1320 + 11 = 1331		Curiosité en 1 et 3. Un cube est égal au produit du nombre par ses deux voisins plus le nombre >>>
11³ = 1331 11⁴ = 14 641 101³ = 1030301 101⁴ = 104060401 110³ = 1331000 110⁴ = 146410000			Motif avec les cubes et les bicarrés. Mêmes chiffres de chaque côté de l'égalité, dans le même ordre, aux zéros près. Même motif avec le carré, mais pas avec les puissances supérieures à 4.
11³ = 1 331 = 1 030 + 301 = 1 120 + 211 = 1 210 + 121 = 1 300 + 31	Cube avec nombres ajoutés à leur retourné. Cinq cas de 1000 à 100 000. Voir 122 + 221= 343 = 7³.
11⁴ = 14 641 = 10 340 + 4 301 = 11 330 + 3 311 = 12 320 + 2 321 = 13 310 + 1 331 = 14 300 + 341	Puissance quatrième de 11 avec nombres ajoutés à leur retourné. Cinq cas de 1000 à 100 000. Voir 164 + 461 = 625 = 5⁴.
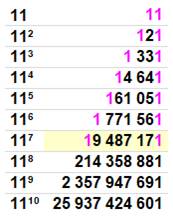
11⁷ = 19 487 171	Plus grande puissance de 11 dont les chiffres extrêmes sont des "1". Notez que les puissances de 1 à 4 sont palindromes. Sa puissance 8 contient trois "8". Le plus petit cas.
11¹¹ = 285 311 670 611		Ses diviseurs, exemple de calcul. C'est le plus grand nombre écrit avec quatre "1". Non, ce n'est pas 1111.
11ⁿ 11² – 1 = 120 11³ – 1 = 1330 = 10 x 133		Toutes les puissances paires de 11, moins 1, sont divisibles par 120. Sinon (impair): divisible par 10.
du¹¹ = … du pour u = 1 ou 9		Conservation des deux derniers chiffres
2¹¹ – 1 = 2 047 = 23 x 89		Nombre de Mersenne composé: plus petit cas pour lequel ce nombres est composé, alors que l'exposant est premier. Nombre de Mersenne avec exposant premier. Le plus petit comportant deux facteurs.
3^{11 – 1} 1 mod 11²		Plus petit premier pour ce motif; le suivant est 1 006 003 – Ribenboim
		Mêmes chiffres de part et d'autre de l'égalité.

Autour du nombre

1/11 = 0,090909…	Seul nombre premier de période 2. Nombre premier unique.
11 + 10 + 6 + … + 2 + 1 = 11 x 12 / 2 = 66	La somme des entiers jusqu'à 11 est un repdigit. Le deuxième exemple parmi trois connus.
1, 1, 1, 1, 2, 3, 6, 11, 23, 47, …	Quantité d'arbres non étiquetés à sept sommets (unlabeled trees).
11 carrés consécutifs 18² + 19² +…+ 28² = 77²	La somme de 3, 4, … ou 10 carrés n'est jamais un carré. Avec 11 carrés c'est possible (comme avec 2).
11 = 56 – 45 1111 = 56² – 45² …	Motifs produisant une persistance du 11.
	Nombre pour lequel la série harmonique dépasse la valeur 3.
11^e nombre triangulaire: 66 1111^e : 617 716 111 111^e : 6 172 882 716 11 111 111^e : 61 728 399 382 716	Nombres triangulaires de même format pour des rangs en repunits.
	Nombre d'or et son inverse.
11! + 1 = 39 916 801	Factorielle plus 1 donne un nombre premier.
	Le quatrième nombre premier de cette forme.
11 k	Longueur d'une arête, au moins, d'une brique de Pythagore.
sin (11) = 0,99999020…	du fait que 7Pi/2 = 10,9955 …
11 \| 10¹¹⁺¹ – 1	Cas de divisibilité aussi observé pour: 3, 9, 11, 33, 77, 99, 143, 303, 369, 407, 707, 959, 1001, …

Jeux – Amusements – Curiosités

11 x 11 = 121 111 x 111 = 12321 1111 x 1111 = 1234321 …		Motif répétitif: carré des repunits créant les pannumériques palindromes.
11 = 2 + 9 x 1 111 = 3 + 9 x 12 1111 = 4 + 9 x 123 …		Motif répétitif.
11 x 91 = 1001 101 x 9901 = 1000001 1001 x 999001 = 1000000001 …		Motif répétitif.
11 = 99 / 9		Faire 11 avec k chiffres identiques.
		Comment faire 11 avec des puissances de 2.
	Jeu du quatre 4. Plus petit nombre non exprimable avec les quatre opérations classiques et la concaténation. Il faut introduire la racine carrée. Il est possible de faire 11 avec trois "4" (44/4 = 11). Il existe une solution avec quatre "4" en introduisant le carré: (4 + 4² + 4!) / 4 = 11

Le jeu du Piquet à cheval ou bataille des nombres

Jeu très ancien qui se joue à deux et qui a une stratégie gagnante pour qui connait le truc.

Tour à tour, les joueurs annoncent un nombre plus petit que 11. Ils sont additionnés et le premier qui arrive à 100 à gagner.

Pour gagner, il faut rallier un des nombres de la liste 12, 23, 34 … (+ 11 à chaque fois).

Fractions

	Développement décimal de période 2 et avec cinq types de décimales. 1/11 = 0,090909…; 2/1 = 0,181818…; etc.
	Fractions amusantes avec 11.
11² = 1 2 1 111² = 12 3 21 1111² = 123 4 321 11111² = 1234 5 4321	Carré de repunits produisant des palindromes.
6² – 5² = 11 56² – 45² = 1111 556² – 445² = 111111 5556² – 4445² = 11111111	Différence de carrés produisant des repunits. Voir Propriétés des nombres impairs
	Nombre d'or à la puissance 5.

Décimales

		Nombre métallique d'ordre 11. Nombre d'or à la puissance 5.
11,14… °		Angle constant dans la figure du carré et du pentagone à côté commun.
11, 7 teslas	Champ magnétique de l'aimant du plus grand appareil d'IRM qui sera mais en service en 2019. Aimant de 130 tonnes. Centre de recherche Neurospin à Saclay (Essonne). Observation du cerveau. Champ = 223 000 fois celui de la Terre.