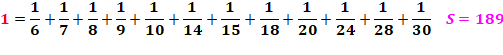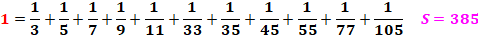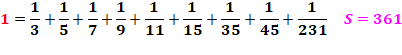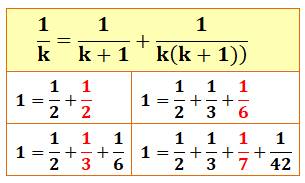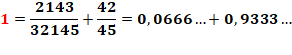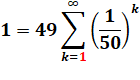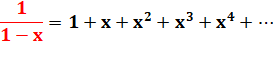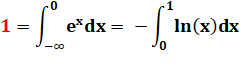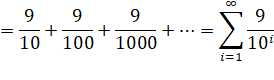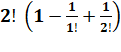Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 03/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	-0-	-1-		-2-	-3-		-4-	-5-	-6-	-7-	-8-	-9-

Nombre 1	Culture 1	Maths 1	De 1 à 1,5	Expressions en 1
Débutant 1	Culture 1 suite	Unité	De 1,5 à 1,9	Proverbes en 1
Quiz 1	Quantité 1	Racines de 1	Fractions = 1
Sciences	Repunit	Nombres en 1	Fractions Unitaires	Horloge maths

Un

One

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1
Bases	/
Romain	I

Suite

Caractérisation du nombre

Catalan

Dihédral

Factorion (1! = 1)

Fibonacci

Heegner

Idonéal

Impair

Intouchable

Ni premier, ni composé

Non premier

Pascal

Unité

Départ de nombreuses suites

Géométrique

Carré, cube …

Pentagonal …

Premier nombre géométrique

Triangulaire

Le nombre 1 est le départ de nombreuses suites non référencées ici.

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

En bonne arithmétique: Un plus un égale tout et deux moins un égale rien. Ninon de Lenclos (1616-1706) Femme de lettres En arithmétique de maternelle: Un poussin égale deux.

Voir Pensées & humour

PROPRIÉTÉS MATHÉMATIQUES générales

Général	Le nombre 1 est souvent dénommé l'unité. Ne pas confondre avec chiffre des unités. Tous les entiers naturels sont atteints en ajoutant 1 au précédent: Nn+1 = Nn= + 1. Le nombre 1 présente beaucoup de propriétés comme le départ de suites. Pour ces raisons, le "1" est parfois appelé nombre lassant. Il faut souvent l'éliminer pour énoncer une propriété.
Nombre	1, 3, 5, …, 2n + 1 Nombres impairs: reste 1 lorsque divisés par 2.	>>>
	1 n'est ni premier ni composé C'est une convention pour obtenir des énoncés de théorèmes plus généraux.	>>>
	1 = 3^2 – 2^3 = 9 – 8 Seule différence de deux puissances égales à un.	>>>
	1 + 11 + 111 + … = K / 81	>>>
Numération	0 et 1 : chiffres de la numération binaire.	>>>
	Loi de Benford: le premier chiffre dans une collection de nombres est le plus souvent un 1.	>>>
Suite	1 et 2: nombres de la suite de Kolakoski.	>>>

Arithmétique	a × 1 = a a / 1 = a a^1 = a 1^a = 1 Log 1 = 0 1! = 1 Seul entier qui produit plus par addition que par multiplication. Le 1 est l'élément neutre de la multiplication. Seul entier égal à son inverse. Seul entier qui divise tous les autres.	>>>
	…1 × …1 = …1 Le produit de deux nombres se terminant par 1 se termine lui-même par 1. Sauf à l'infini, où 1 est une limite possible parmi d'autres: la valeur de "un puissance infinie" est indéterminée.	>>> >>>
	Une fraction avec un 1 au numérateur est une fraction unitaire base des fractions égyptiennes.	>>>
	La quantité minimale de 1 nécessaire pour écrire un nombre est appelée: complexité du nombre.	>>>
Algèbre	1^-5 = 1^-1 = 1^0 = 1^1 = 1^5 = 1^k	>>>
	1 = 2 Démonstration (erronée!).	>>>
	– 1 = i² Fondement des nombres complexes.	>>>
Théorie des nombres	– 1 Nombre de Heegner.	>>>
Trigonométrie	sin (90°) = tg (45°) = cos (0°) = 1 Valeurs trigonométriques. Ces cinq fonctions sont égales à 1 pour un angle nul: cos, cosh, sec, sech et exp.	>>>
Géométrie	r = 1 rayon du cercle inscrit dans le triangle de Pythagore (3, 4, 5)	>>>

PROPRIÉTÉS MATHÉMATIQUES détaillées

Fractions donnant 1

1	Nombres bons. Nombres parfaits. Somme des inverses des chiffres. Nombre non-congruent.
1 = 1/3 + 1/3 + 1/3 1 = 1/2 + 1/4 + 1/4 1 = 1/2 + 1/3 + 1/6	Sommes de trois fractions égyptiennes égales à 1. Les trois seules à trois termes
1 = 1/4 + 1/4 + 1/4 + 1/4 1 = 1/3 + 1/4 + 1/4 + 1/6 1 = 1/3 + 1/3 + 1/6 + 1/6 1 = 1/2 + 1/6 + 1/6 + 1/6 1 = 1/2 + 1/4 + 1/6 + 1/12 1 = 1/2 + 1/3 + 1/7 + 1/42	Sommes de quatre fractions égyptiennes égales à 1. Il en existe quatorze à quatre termes dont quatre avec des dénominateurs distincts et parmi ces quatre "42" est le plus grand dénominateur.
1 = 1/5 + 1/5 + 1/5 + 1/5 + 1/5 1 = 1/4 + 1/4 + 1/6 + 1/6 + 1/6 1 = 1/3 + 1/4 + 1/5 + 1/6 + 1/20	Sommes de cinq fractions égyptiennes égales à 1. Il en existe 147 à quatre termes. La plus petite à dénominateurs distincts.
		Solutions avec12, 11 et 9 fractions égyptiennes. S = somme des dénominateurs.
	Le tableau montre une procédure permettant d'obtenir une infinité de sommes de fractions égales à 1 >>> Voir Brève 51-1012

1 = 1/5 + 1/3 + 7/15 = 0,2 + 0,333 + 0,466	Fraction donnant un entier.
	Deux des innombrables sommes de deux fractions dont la somme est 1, et utilisant les nombres de 1 à 5.
1 = 1/2 + 1/4 + 1/8 + 1/16 + …	Car: 1 + x + x² + x^3 + … = 1 / (1-x) pour x < 1 Ici cas où x = ½ Voir p-adiques
	Fraction limite égale à 1.
	Sommation avec des factorielles.
	Somme infinie pour 1. Produit avec suite des nombres pairs. Voir Formation des décimales de 1/7

Formules donnant 1

	Développement dont tous les coefficients sont à 1 (série génératrice).
1 = a² – (a – 1) (a + 1)	Relation entre 1 et le carré de tout nombre.
1 = sin² A + cos² A	Quel que soit l'angle A. Voir Pythagore retrouvé.
1 = 1^3 + 1^3 + (–1)^3 = 9^3 + (– 6)^3 + (– 8)^3 = 729 + (– 216) + (– 512)		Sommes de trois cubes.
1 = (9n^4)^3 + (3n – 9n^4)^3 + (1 – 9n^3)^3	Infinité de somme de trois cubes pour 1. Formule trouvée en 1936 par Kurt Mahler.
	Voir Explications.
1 = ½ (1 – i) (1 + i)	Nombres complexes.
	Relation d'Euler.
1 =	Nombre d'or et son inverse.
	Aire sous les courbes de ces deux fonctions.

Fonctions arithmétiques

1 = 100 %	Notation de cent pourcent.
1 = 0,999 …infinité de 9	Voir Explications.
1 = 1^0 = 1^1 = 1^2 = 1^3 = 1^n	Voir Impairs, carrés et cubes.
1 = racine continue de 0	Ou, comment faire un nombre avec 0.
de 0 à 1	Valeurs limites d'une probabilité.
de – 1 à + 1	Valeurs limites du sinus et du cosinus.
1 = !2 =	Sous-factorielle de 2.
20 = 2^2 x 5^1 (2 + 1) (1 + 1) = 6	Produit des exposants +1 = quantité de facteurs d'un nombre. Exemple avec 20: ce nombre a six diviseurs: 1, 2, 4, 5, 10 et 20.

Jeux et curiosités

+ 1	En ajoutant 1, Euclide prouve qu'il existe une infinité de nombres premiers.
1 = 2 ?	Démonstrations fausses.
1 est	Point d’aboutissement de la séquence de Syracuse.
111…1	Est appelé repunit. On en connaît seulement 5 premiers, dont 11.
11 x 11 = 121 111 x 111 = 12321 1111 x 1111 = 1234321		Multiplications de repunit.
	Seule somme pannumérique de trois fractions avec un chiffre au numérateur et deux au dénominateur.
1/1 = 2/2 = ... = 9/9	Le plus petit entier écrit avec 2 chiffres et non 10, réponse le plus souvent donnée à cette question. Le plus petit nombre serait: 0,1et non pas 1/9 = 0,1111…
11^11 = 2,8… 10^11 = 285 311 670 611 1111! = 1,6… 10^2 903 (11^11)! = 10^???		Le plus grand nombre avec quatre 1, sans autres signes. On trouve plus grand avec signes: factorielle et plus grand encore avec parenthèses. >>>
1 = 35 – 3² – 5² = 75 – 7² – 5²	Ce motif n'existe que deux fois avec 1. Voir Curiosité
1 = Ö4 Ö4 / 4 x 4/4	Faire 1 avec cinq 4. Voir Faire 1 avec k chiffres identiques.
1 = ½ [ (a²)^0 + 1 ]	Curiosité. Ce type de formulation peut servir dans les calculs de simplification et généralisation.
1, 1, 1, …	La conjecture de Gilbreath énonce que la première ligne de son tableau est formée de 1.

Logarithmes, puissances, dénombrement …

1 = 3^2 – 2^3	Seul cas de différence de puissances égale à 1.
1 = n² – (n – 1) (n + 1)	Différence entre carré et produit des nombres adjacents. >>>
1 = a² – k.b² = 97² – 3 x 56² (exemple)	Propriété de certains nombres exploitée par Brahmagupta.
1 = 10^3 + 9^3 – 12^3 = 1000 + 729 – 1728	Somme de trois cubes. Voir La formulation générale.
00...01	Puissances terminées par 1.
est indéterminé	1 x 1 x 1 x … x 1 = 1 est une valeur possible, mais il y en a d'autres.
	Somme des inverses de toutes les puissances pures. Formule démontrée par Goldbach.
	Valeur réelle de cette expression >>>
1 = log10 (2) + log10 (5) = 0,3010 ... + 0,6989... = log10 (2,5) + log10 (4) = etc.	Somme de log = log du produit et log10 (10) = 1
1 = log a a = log e e = log b a / log a b = 1 ^0 = e ^0 = a ^0	Zéro, infini … Logarithmes / Calcul des log
	Découle directement de l'identité d'Euler portée à la puissance 2k.
1 = 2^n . 4^-2n . 8^n = (a^x )^y - z . (a^y )^z - x . (a^z )^x - y = …	Puissances.
1 = An^0 = Cn^0	Arrangements et Combinaisons.

Nombre – 1 et imaginaires

– 1	Premier nombre entier relatif négatif. Nombre de Heegner.
– 110 = 11112	En binaire informatique, le 1 initial indique que le nombre est négatif. La valeur – 1 est codée avec tous les bits à 1.
	Mais alors, le rapport d'une quantité petite à une grande est égal à celui d'une grande à une petite : paradoxe émis du temps de Pascal par Antoine Arnauld.
	Relation d'Euler.
	Base des nombres imaginaires ou complexes. Certains préfèrent dire: i² = –1.
	Une des trois racines cubiques de l'unité.

Tableau des racines complexes de 1 et – 1 pour les racines carrée, cubique et bicarrée

Voir Racines de l'unité

Décimales

Voir Pages dédiées >>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]	Repdigit (Brésilien)
/	/

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombres de 1 à 1,5
Voir	Débutants – Index Départ de nombreuses suites Nombres – Glossaire Premier nombre géométrique
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/UnP11.htm