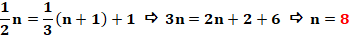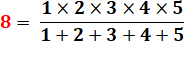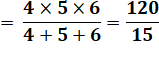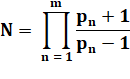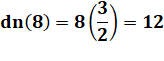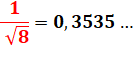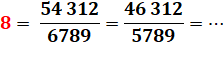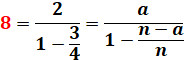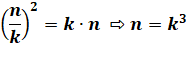|
Édition du: 03/04/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
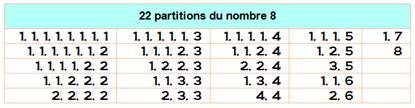
Plus petit cube. Seul à un
chiffre. |
Voir Partitions |
|||
|
Caractérisation
du nombre
|
|
Voir |
||
|
Amusement L'infini
tourné d'un quart de tour devient huit
Voir Infini Humour
Voir Humour |
||||
Rappel
Propriétés générales >>>
![]()
PROPRIÉTÉS TYPIQUES
|
|
||
|
8 est un cube. Nombre de Leyland |
||
|
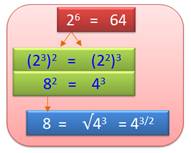
Seule puissance qui en
précède immédiatement une autre. |
||
|
Propriété de tous les
nombres divisibles par 4. |
||
|
|
||
|
Seul nombre de
Fibonacci à être un cube. |
||
|
|
|
par ses trois derniers
chiffres l'est. |
||
|
Exemple: 3² = 9 = 8 + 1; 5² = 25 = 3 x 8 + 1 … |
||
|
|
Voir Jeux en
section culturelle
![]()
Numération – Chiffres – Dénombrement
|
8 =
7 x 1 + 1 |
|
|
8 =
1x2 + 2x3 |
|
|
8 x 12 345 679 = 98 765 432 |
|
|
8T = A² – 1 |
|
Addition
Diagramme de Ferrers du nombre 8
Voir Diagramme
de Ferrers
|
8 =
3 + 5 = 2 (1 + 3) |
Seule somme
de premiers impairs consécutifs jusqu'au moins le millionième.
|
|
8 =
3 + 5 = 1 + 1 + 2 + 4 = 1 x 1 x 2 x 4 |
|
|
8 =
4 + 4 et 4 x 4 = 16 |
|
|
8 = 1 + 1 + 2 + 4 = 1 + 1 + 2 + 2 + 2 = 1 x 1 x
2 x 4 = 1 x 1 x 2 x 2 x 2 |
|
|
8
= 1 + 2 + 5 = 1 + 3 + 4 |
|
![]()
Multiplication
Table
de multiplication du 8

Voir Table
complète
|
8 x
… |
|
|
8 =
2 x 2² |
|
|
8 =
3 x 2² – 2 x 2
|
|
|
8 =
(2+1) + (2–1) + (2x1) + (2/1) |
|
|
8 =
(3² – 1) = (3 –
1)(3 + 1) = 2 x 4 |
|
|
8 |
|
![]()
Division
|
Question: quel est le nombre n tel que sa moitié excède
le tiers du nombre suivant d'une unité ? Réponse:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dn(8) = 12
|
Plus petit nombre dont les dérivées
numériques successives vont en croissant: |
|
|
|
|
8 = |
|
|
|
|
|
4 = 2² |
|
|
(2k
)² = 8a + r avec r = {0,4} (2k + 1)² = 8a
+ r avec r = {1} |
|
|
n |
|
|
32n + 7 est divisible
par 8 (2k+1)2n + 7 est divisible par 8 |
Exemples
|
|
8 = 22+1 = 32^1 – 1 |
|
![]()
Puissances
À noter
ce rapprochement curieux entre fractions
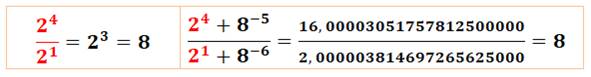
Voir Comment
calculer la fraction de droite
|
8 =
23 = 22 + 22 = 3² – 1 = 9 – 1 |
|
|
8 = 22 . 2 9 = 32 |
|
|
|
|
|
8 =
3² –
1 = 4 + 4 = 1 x 2 x
4 = 2 x 4 |
|
|
8 =
11 + 12 + 21 + 22 |
|
|
8 = 13 + 22 + 31
= 1 + 4 + 3 |
|
|
8 =
3² – 1² |
|
|
8 =
4² – 2² |
|
|
8 =
24 – 23 = 16 – 8 |
|
|
8 =
3122 – 463 = 97 344 – 97 336 |
|
|
32 – 1 = 8 34 – 1 = 80 36 – 1 = 728 38 – 1 = 6560 … |
|
|
8 cubes pour tout nombre sauf 23 et
239 |
Tout
nombre est la somme d'au plus neuf cubes. En fait, tous sont somme de huit
cubes sauf 23 et 239. |
Puissances du nombre

|
|
Racine de 8 = 2,828427124746190097… Inverse = 0,353553390593273762… |
|
83 = 512 & 5 + 1 + 2 = 8 53 = 125 |
|
|
82 = 64
86 = 262 144 83 = 512
87 = 2 097 152 84 = 4
096 88
= 16 777 216 |
|
|
63 7 |
|
|
|
|
|
856 = 374…001 856 |
|
Autour du nombre
|
…8 ou …6 |
|
|
– 8 = (1 + i
= (1 + i)4 + (1 – i)4
= (1 + i)5 + (1 – i)5 |
|
|
e8
= 2980,958 … e8
– 2981 = - 0,04201… |
|
|
|
|
|||||
|
8 =
4 + 4 + 4 – 4 |
|
|||||
|
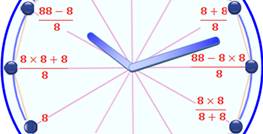
8
+ 8 + 8 + 88 + 888 = 1 000 |
|
|||||
|
|
Notez que 8 + 8 = 4 sur l'horloge. |
|||||
|
= 5 / 0,555… – 5
/ 5 |
||||||
|
8 x
473 = 3 784 |
|
|||||
|
8 x
11 498 = 91 984 8
x 113 967 = 911 736 8
x 114 898 = 919 184 … |
|
|||||
|
8
x 123 456 79 = 98 765 432 8
x 123 456 789 = 987 654 321 – 9 |
|
|||||
|
|
|
|||||
|
8 x 8 + 13
= 77 8 x 88 +
13 = 717 8 x 888 +
13 = 7117 8 x 8888 +
13 = 71117 …. |
12 x 8 + 2 = 98 123 x 8 +
3 = 987 1234 x 8 +
4 = 9876 12345 x 8
+ 5 = 9876 … |
|
||||
|
|
|
|||||
|
8 = 4! / 3 = 24 / 3 |
|
|||||
|
888 = 98 x 9 + 6 … |
|
|||||
|
(9–5) + (6/3) =
(1+7) = 4x2 |
|
|||||
|
8
=> 4² = 16 & 2 x 8 = 16
Pour k = 2 => n = 23 = 8 Pour k = 3 => n = 33 = 27 |
|
|||||
|
8,0000000729… = 987654321 /
123456789 = 8 + 9 / 123456789
|
||
|
8,000349495… = ln 42 + ln 71 |
|
|
|
8,1212… 7,1212…4 +
8,1212…4 |
|
|
|
|
|
|
|
|
|
|
|
8, 539 734 222 ... = |
|
|
|
8,7000366252… ≈ 87/10 |
Rayon du
cercle limite inscrit dans l'emboitement des polygones réguliers successifs. |
|
|
8,794 143" |
Précis: c'est l'angle plan sous-tendu par le
rayon équatorial de la Terre à une
distance d'une unité astronomique de longueur qui, depuis 2012, est une unité
conventionnelle de longueur égale à 149 597 870 700 mètres. |
|
|
8,888… = 80/9 |
||
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
|
|
2, [1, 0, 0, 0] 3, [2, 2] 4,
[2, 0] 5,
[1, 3] |
6,
[1, 2] 7, [1, 1] 8,
[1, 0] |
3,
[2, 2] 7,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()