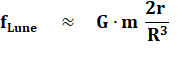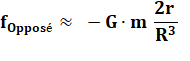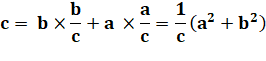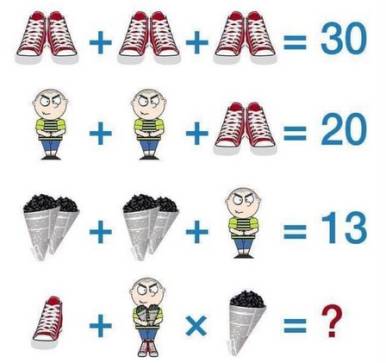NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 23

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

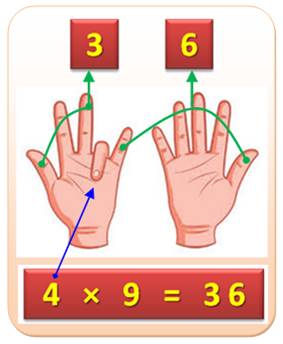
440. Multiplication par 9
Pour calculer 4 x 9, rien de plus simple avec les doigts: Les deux mains face à vous. Les doigts sont numérotés de 1 à10. Plier le doigt n°4. Les doigts levés à gauche donnent le chiffre des dizaines: 3. Les doigts levés à droite indiquent le chiffre des unités: 6. Alors 4 x 9 = 36. Évidemment, cela marche pour toute la table de multiplication du 9.
Brèves associées	>>> Multplication par 11, 111 … >>> muliplications avec les doigts		>>> Tables de multiplication en brèves
Pour en savoir plus	>>> Multiplications avec les doigts		>>> Tables de multiplication

441. Multiplication par 7
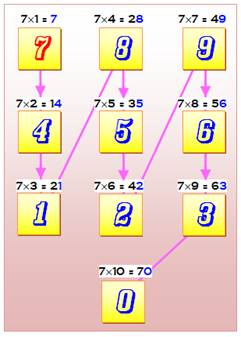
Un schéma simple permet de se représenter les unités des multiplications par 7. Pensez au clavier de votre ordinateur ou de votre calculette. Partez du 7 et parcourez les chiffres de haut en bas et de gauche à droite, vous balayez les unités des multiplications par 7. En effet: 7 x 1 = 7 et le suivant est bien 7x 2 = 14 se terminant par 4. Arrivé en bas avec le 1, on constate que 7 x 3 est bien 21 avec un 1 pour unité. Etc.
Brèves associées	>>> Multiplications originales		>>> Multiplication économe pour grands nombres
Pour en savoir plus	>>> Multiplication par 7 >>> Divisibilité par 7		>>> Tables de multiplication

442. Les marées
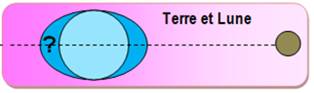
On comprend facilement que la Lune attire l'océan vers elle du fait des forces de la gravitation. Mais pourquoi, elle le repousse de l'autre côté. Les lois de Newton montrent que les forces de part et d'autre de la Terre sont de même intensité mais opposées. Il s'agit du différentiel par rapport à la force exercée au centre de la Terre. Certains invoquent la force centrifuge due à la rotation du couple Terre-Lune. Cette considération est inutile dans un référentiel inertiel. Elle devient une force fictive commode dans un calcul avec référentiel non inertiel (qui serait attaché à la rotation).		Pourquoi une marée de l'autre côté ? Non, ce n'est pas un effet de la force centrifuge. Les forces de part et d'autre
Brèves associées	>>> Quantité de sable dans l'Univers		>>> Boson de Higgs
Pour en savoir plus	>>> Marée >>> Lune		>>> Gravitation >>> Lois de Newton

443. Construction dorée remarquable
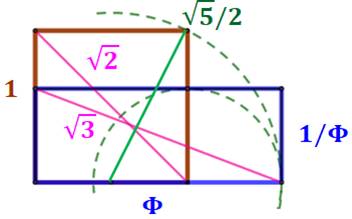
Construction Carré marron. Segment vert joignant un sommet au milieu du côté du carré. Cercles pointillés en vert (le grand, puis le petit). Propriétés de cette figure Aire carré = Aire rectangle Avec carré de côté 1 Diagonale du carré = rac(2) Diagonale du rectangle = rac(3) Longueur du segment vert: rac(5) / 2 Longueur du rectangle = Phi, le nombre d'or Larguer du rectangle = 1/ Phi		Construction d'Euclide
Brèves associées	>>> Arc de cercle sans le centre		>>> Jardinier
Pour en savoir plus	>>> Construction dorée – Explications		>>> Constructions élémentaires

444. Somme ondulante = carré
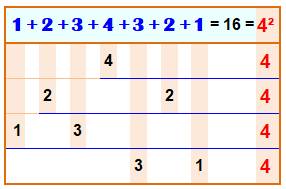
Propriété La somme des chiffres répétés sous forme palindrome est égale au carré du chiffre central. Valable de 2 à 9. 121 => 1 + 2 + 1 = 4 = 2² 12321 => 1 + 2 + 3 + 2 + 1 = 9 = 3² 1234321 => 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 = 4² 123454321 => 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 = 5² … 123…9…321 => 1 + 2 +…+ 9 + … + 3 + 2 + 1 = 81 = 9²		Principe de formation du carré
Brèves associées	>>> Somme de chiffres identique et divisibilité par 9			>>> Palindromes
Pour en savoir plus	>>> Application de cette somme		>>> Nombres ondulants

445. 3-repdigits au cube
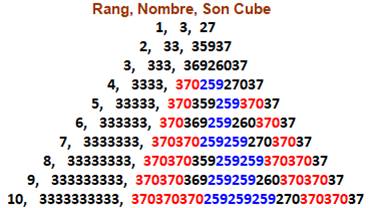
Tous les 3-repdigits (nombres avec 3 uniquement) au cube ne comportent jamais les chiffres {1, 4, 8}. Motif quasi-symétrique en (370) (259) (370).
Brèves associées	>>> Repdigits en 2 au cube		>>> Nombres uniformes – Repunits
Pour en savoir plus	>>> 3- repdigits >>> k-repdigit et le chiffre k		>>> Nombre 33 >>> Repdigits

446. Théorème de Pythagore
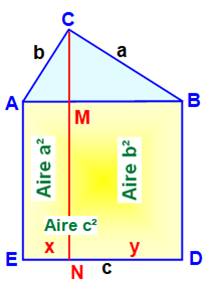
Triangle rectangle ABC. Carré ABDE sur l'hypoténuse. La perpendiculaire issue du sommet C découpe le carré jaune en deux rectangles d'aires a² et b² pour une somme égale à c². Explications Amusant de voir comment les aires a² et b² se retrouvent simplement dans le carré de côté c.
Brèves associées	>>> Théorème de Pythagore – Visuel	>>> Triplets de Pythagore: a² + b² = c²
Pour en savoir plus	>>> Théorème de Pythagore	>>> Triangle rectangle

447. Rétablir l'addition
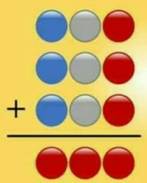
Résoudre cette opération où chaque couleur représente un chiffre. Solution Unités: 0 + 0 + 0 = 0 ne convient pas car la somme serait nulle. 5 + 5 + 5 = 15 convient avec retenue de 1. Dizaines: 3d + 1 = …5 => d = 8 avec 2 de retenue. Centaines: 3c + 2 = 5 = > c = 1. Bilan: 3 x 185 = 555.
Brèves associées	>>> Opérations mystérieuses	>>> Brèves et énigmes – Index
Pour en savoir plus	>>> Compléments sur cette addition	>>> Nombre 555

448. Partager le triangle en six parts égales
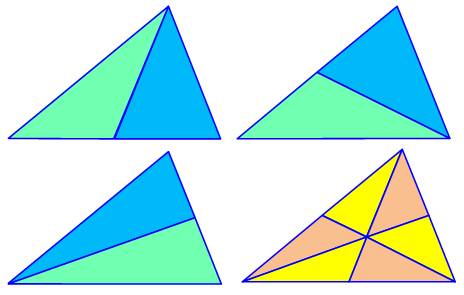
Un triangle quelconque. Ses trois médianes le découpent en six triangles moyens et six petits triangles. Les trois couples de triangles (verts et bleus), avec un sommet commun et des bases égales à la moitié du côté, ont chacun la même aire. Les six triangles (jaunes et marron) ont la même aire.
Brèves associées	>>> Partage du triangle en k parts égales		>>> Triangle inscrit dans le rectangle
Pour en savoir plus	>>> Partage du triangle en parts égales		>>> Triangle et médianes

449. Divisibilité de a^n – b^n
Cas général L'expression a^n – b^n est toujours divisible par (a – b) a^2 – b^2 = (a – b) (a + b) a^3 – b^3 = (a – b) (a² + ab + b²) a^4 – b^4 = (a – b) (a + b) (a² + b²) Ex: 7^n – 3^n divisible par 7 – 3 = 4 => 7² – 3² = 40; 7^3 – 3^3 = 316 7^n – 6^n divisible par 7 – 6 = 1, et par 7 + 6 = 13 si n est pair => 7² – 6² = 13; 7^4 – 3^4 = 1105 = 13 x 85 Cas où b = 1; où il est question de repdigits Le développement montre qu'un nombre à une puissance auquel on soustrait un, est un nombre composé; et, il s'écrit comme un repdigit dans la base puissance moins un. C'est un nombre brésilien.
Brèves associées	>>> Identités remarquables	>>> Identité de Brahmagupta
Pour en savoir plus	>>> Divisibilité de a^n – b^n >>> Puissances	>>> Nombre brésilien >>> Repdigit >>> Base de numération

450. Multiplication à traits
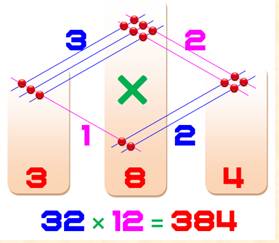
Pour calculer 32 x 12, Posons 3 et 2 allumettes parallèles et en tas espacés Puis, posons 1 et 2 allumettes en oblique. Notons les croisements par un point. Avec cette disposition, trois alignements verticaux de points se dessinent. Pour connaitre le résultat de la multiplication, il suffit de compter les points dans chaque colonne. La multiplication devient une addition classique, avec ses retenues le cas échéant.
Brèves associées	>>> Multiplication à la russe (sans table)		>>> Multiplication par 9 – Avec les doigts
Pour en savoir plus	>>> Multiplication à traits, chinoise …		>>> Multiplication – Initiation

451. Énigmes virales
Une des innombrables énigmes que vous trouverez sur Internet. L'auteur prétend que seul 2% de la population est capable de la résoudre. Alors les internautes propagent le défi. C'est pourquoi, une telle énigme est dite virale. Sa résolution semble simple. On propose rapidement une solution. Elle est majoritairement fausse. Il faut compter avec l'esprit retors des auteurs. Saurez-vous déjouer les pièges? Un conseil, je ne ferais pas très confiance à ce petit bonhomme ! Solution
Brèves associées	>>> Égalité en 71 à rectifier		>>> Les trois filles
Pour en savoir plus	>>> Cette énigme et d'autres		>>> Jeux et énigmes – Index

452. Fractions avec brique à jouer
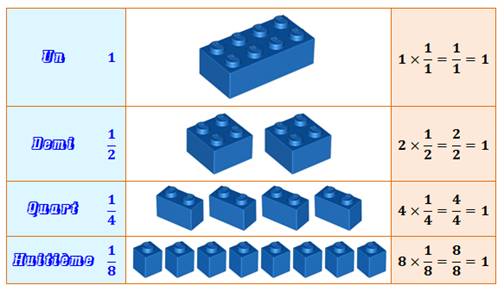
La brique de base représente une unité. Ici elle possède huit emplacements propices à définir quelques fractions. La brique de base est FRACTIONNÉE en 2, 4 ou 8. Fractionnée en deux, on obtient deux demi-briques; lesquelles emboitées sur la brique de base, la couvrent complètement: deux demis égal un.
Brèves associées	>>> Fractions en boucle avec trois chiffres		>>> Division
Pour en savoir plus	>>> Fractions et briques type Lego		>>> Fractions – Initiation

453. Pions en cercle – Énigme
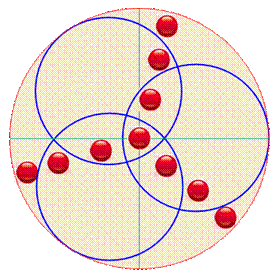
Comment encercler dix pions avec trois cercles ? Un cercle et dix pions disposés en Y. Comment, avec trois cercles, isoler chacun des pions. Énigme parfois habillée de la manière suivante: un enclos circulaire et dix chèvres, comment les isoler avec trois enclos circulaires? On vérifie bien que les 10 billes sont dans chacune des 10 régions.
Brèves associées	>>> Énigme du parking		>>> Le fortin et ses gardes
Pour en savoir plus	>>> Cette énigme et d'autres		>>> Cercle – Propriétés

454. Anagrammes des nombres
Deux chiffres distincts 12, 4, {1, 2, 12, 21} Deux chiffres identiques 33, 2, {3, 33} Trois chiffres distincts 123, 15, {1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132, 213, 231, 312, 321} Trois chiffres dont deux identiques 445, 8, {4, 5, 44, 45, 54, 445, 454, 544} Trois chiffres identiques 666, 3, {6, 66, 666} Quatre chiffres identiques 5555, 4, {5, 55, 555, 5555}		Quatre chiffres distincts 1234, 64, {1, 2, 3, 4, 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43, 123, 124, 132, 134, 142, 143, 213, 214, 231, 234, 241, 243, 312, 314, 321, 324, 341, 342, 412, 413, 421, 423, 431, 432, 1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321} Quatre chiffres avec deux répétés 5567, 34, {5, 6, 7, 55, 56, 57, 65, 67, 75, 76, 556, 557, 565, 567, 575, 576, 655, 657, 675, 755, 756, 765, 5567, 5576, 5657, 5675, 5756, 5765, 6557, 6575, 6755, 7556, 7565, 7655} Quatre chiffres avec deux et deux répétés 3344, 18, {3, 4, 33, 34, 43, 44, 334, 343, 344, 433, 434, 443, 3344, 3434, 3443, 4334, 4343, 4433} Quatre chiffres avec trois répétés 1112, 13, {1, 2, 11, 12, 21, 111, 112, 121, 211, 1112, 1121, 1211, 2111}
Brèves associées	>>> Anagrammes des nombres – Compter		>>> Permutations alternées
Pour en savoir plus	>>> Anagrammes numériques		>>> Nombres multi-premiers

455. Partitions strictes

Partitions du nombre 6 (comme 1 + 5 = 6)

Partitions						T	I	D
1	1	1	1	1	1	1	1
	1	1	1	1	2	2
		1	1	2	2	3
			2	2	2	4
		1	1	1	3	5	2
			1	2	3	6		1
				3	3	7	3
			1	1	4	8
				2	4	9		2
				1	5	10	4	3
					6	11		4

On compte: T = 11 partitions du nombre 6, dont
I = 4 sont composées de nombres impairs, et
D = 4 sont composées de nombres distincts.

Propriété

Quantité de partitions STRICTES

= quantités de partitions IMPAIRES

Quantité

1 à 9	1, 1, 2, 2, 3, 4, 5, 6, 8,
10 à 19	10, 12, 15, 18, 22, 27, 32, 38, 46, 54,
20 à 29	64, 76, 89, 104, 122, 142, 165, 192, 222, 256,

Exemples
n = 10, il y a 10 partitions strictes
n = 19, il en a 54.

Et, autant pour les partitions en nombres impairs.

Brèves associées

>>> Partitions et décompositions

>>> Partitions – Index

Pour en savoir plus

>>> Partitions strictes

>>> Diagramme de Ferrers-Young

456. Puissances et mêmes chiffres
Nombres tels que ses chiffres se retrouvent dans une de leurs puissances, sans autres chiffres. Le nombre 4 762 est le plus petit tel nombre pour un carré. évidemment certains chiffres sont répétés dans le carré. Le suivant est: 4 832² = 23 348 224. Le plus petit pour une cube: 107 624^3 = 1 246 600 760 666 624 La recherche est un excellent exercice de programmation ne présentant pas de grande difficulté.			Les mêmes chiffres de chaque côté
Brèves associées	>>> Carré = Somme de cubes	>>> Carré et cube à la fois
Pour en savoir plus	>>> Puissances qui ont les mêmes chiffres que le nombre

457. Tenségrité
Tenségrité: faculté d'une structure à se stabiliser par le jeu des forces de tension et de compression qui s'y répartissent et s'y équilibrent. Occasion de construction de jouets en bois ou en briques de construction. Cette structure (illustration) ne tient que par ces trois chainettes (pas d'aimants !).
Brèves associées	>>> Quantité de sable dans l'Univers		>>> Sciences – Index des brèves
Pour en savoir plus	Votre moteur de recherche préféré; voir les vidéos

458. Somme des premiers – Goldbach
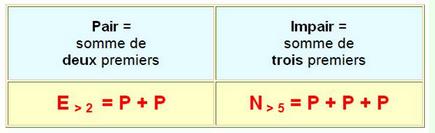
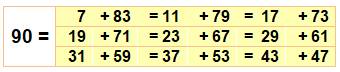
Christian Goldbach (1690-1764) propose une propriété qu'il ne sait pas démontrer, une conjecture. Aujourd'hui encore elle reste sans preuve. Tout nombre pair est la somme de deux nombres premiers. Également, tout nombre entier est somme de trois nombres premiers. Pas de preuve, mais une forte présomption car chaque nombre est somme de multiples fois. Le nombre 90 est neuf fois somme de deux premiers. Le nombre 990 l'est 52 fois. Exemples: 10 = 3 + 7 ; 100 = 47 + 53.		Un passage est constitué de plots numérotés avec tous les nombres entiers. Nous disposons de deux passerelles au choix avec des nombres premiers comme longueur. Alors, nous pourrons rejoindre n'importe quel plot numéroté. Il existe même neuf choix possibles pour atteindre le plot 90.
Brèves associées	>>> Nombres premiers		>>> Partitions et décompositions
Pour en savoir plus	>>> Conjecture de Goldbach >>> Tables de sommes de premiers		>>> Sommes de premiers consécutifs

459. Nombres premiers résistants
Le plus grand premier résistant (tronquable) par la droite: 73 939 133 Ce nombre est premier et si on l’ampute par la droite, il reste premier. Coquetterie: Nombre de 8 chiffres, 8 fois premier. Record par la droite: 73 939 133 – Ils sont 83. Record par la gauche: 357 686 312 646 216 567 629 137 – Ils sont 260..		73 939 133 73 939 13 73 939 1 73 939 73 93 73 9 73 7 Ces nombres, obtenus par effacement du chiffre de droite, restent premiers
Brèves associées	>>> Nombres premiers	>>> Type de nombres – Index Brèves
Pour en savoir plus	>>> Premiers résistants	>>> Nombre 73 939 133

Retour	Brèves de maths – Page 22
Suite	Brèves de maths – Page 24
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve23.htm