|
Édition du: 07/12/2021 |
|
INDEX |
Restes Chinois |
|||
![]()
|
Nombres 45, 454, 4545 et 45454 Quel est
le plus petit nombre n tel que n divisé par 45, 454, 4545 et 45454 donne pour
restes respectivement 4, 45, 454, 4545 ? Problème
121 de H.E. Dudeney – 536 Puzzles & Curious Problems. Ce problème est
parfois cité sur Internet, mais jamais avec la manière d'atteindre la
solution. |
||
|
|
Sommaire de cette page >>> En bref, les solutions selon le niveau de
contrainte >>> Méthodes de recherche >>> 1 –
Recherche systématique par ordinateur >>> 21 – Recherche incrémentale: nombres en 4 mod
45 >>> 22 – Nombres en 45 mod 454, en plus >>> 23 – Nombres en 454 mod 4545, en plus >>> 24 – Nombres en 4545 mod 45454, en plus >>> 25 – Nombres en 45455 mod 454545, en plus >>> 3 –
Méthode des restes chinois >>> Deux autres exemples: 3737 et 2323 |
Débutants Glossaire |
En bref, les solutions selon le niveau de
contrainte
|
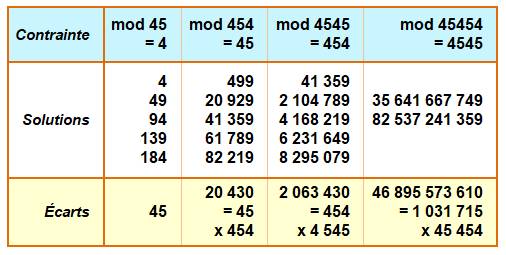
Tableau: chaque colonne
indique la suite des nombres ayant un résidu r modulo m. Exemple: 499 est le plus
petit nombre qui donne à la fois un reste
4 lorsque divisé par 45 et un reste 45 lorsque divisé par 454. L'écart avec
le suivant est 20 430, nombre qui est le produit de 45 par 454 (le PPCM des deux
nombres). La solution au problème 121 de
Dudeney est 35 641 667 749. La réponse n'est pas évidente à trouver !
Voyons cela … |
Voir Nombre
35 641 667 749
|
Recherche On cherche le plus petit nombre qui produit des
restes donnés pour des divisions particulières. Il existe au moins trois méthodes: 1.
Recherche systématique par
ordinateur; 2.
Recherche incrémentale en progressant
d'une contrainte à la suivante; et 3.
Recherche mathématique à l'aide du
théorème des restes chinois. |
Notation
On lit: Le nombre 49 est congru à 4 modulo 45. Ce qui veut
dire: 49 divisé par 45 donne un reste 4; ou encore: 49 = 1 x 45 + 4. Propriété Tous les nombres en 49k produisent le même reste
et sont donc congrus à 4 mod 45. |
|
|
Programme Rédiger un programme de recherche de nombres mod
m est simple, d'autant que tous les logiciels comportent une instruction
calculant directement le modulo. Vrai également pour les tableurs et les
calculettes scientifiques. |
Programme générique Avec n de 1 à 1000 faire FIN |
|
|
Implémentation avec Maple
|
Commentaires Boucle d'exploration du nombre n jusqu'à 100 000. Trois conditions successives. Ce qui évite de
poursuivre les calculs si n ne remplit pas la condition précédente. Impression immédiate du résultat. Beaucoup plus
long pour trouver le nombre qui est demandé avec la division par 45454. |
|
|
Recherche On cherche les nombres n tels que divisés par 45
produisent un reste égal à 4. Le nombre 4 est le plus petit, évidemment. Le suivant sera 4 + 45 = 49. Tous les autres: 4 + 45k. |
n
= 4 mod 45 4, 49, 94, 139, 184, …. Formule L'équation à satisfaire est: n = 45k + 4 |
|
|
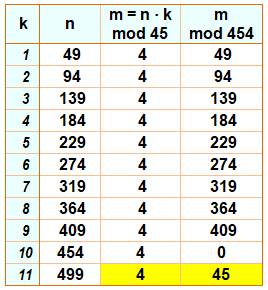
Recherche Pour satisfaire la première contrainte (n = 4 mod 45), le nombre doit
être de la forme 45k + 4. Quelle est la valeur de k pour satisfaire la seconde contrainte (n =
45 mod 454) ? Le tableau montre l'exploration pour les valeurs successives de k
jusqu'à trouver un reste 45 pour k = 11 et n = 499 Équations
Suivants Les nombres 45 et 454 n'ont aucun facteur en commun (PEE) Pour trouver le nombre suivant, il faut que les contraintes 1 et 2
soit satisfaites, donc trouver un multiple commun au deux: c'est le PPCM. Valeur suivante: 499 + 20 430 = 20 929. |
Nombres n ≡ 4 mod 45 & ≡
45 mod 454
En l'occurrence, on aurait pu essayer directement 45 + 454 = 499. Formule |
|
|
Équations n = 45a +
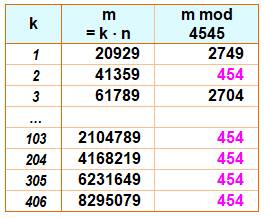
4 n = 454b + 45 n = 4545c + 454 Résolution On sait que les deux premières conditions
conduisent à des nombres de la forme: 499 + 20 430 k. En explorant, la valeur prise pour les k
successifs, on tombe rapidement sur la solution avec k = 2. Suivants Avec 4545 = 45 · 101, PPCM (45, 454, 4545) = 2 063 430 Nombre suivant: 41 359 + 2 063 430 = 2 104 789 |
Formule |
|
|
Équations n = 45a +
4 n = 454b + 45 n = 4545c + 454 n = 45454d + 4545 Résolution Dans la formule précédente, quelle est la valeur
de k pour que le nombre soit égal à 4545 mod 45454. Nous sommes face à de grands nombres et seul un
programme permet de trouver Suivants Avec 45454 = 2 · 22 727 PPCM (45, 454, 4545, 45454) = 46 895 573 610 Formule n = 35 641 667 749 + 46 895 573 610 · k |
Programme Maple
|
|
|
La
recherche incrémentale avec logiciel donne ce résultat: |
n = 94 999 178 227 999 + 473 692 189 034 610 · k |
|
|
Pour comprendre les tableaux qui suivent, il faut
se reporter à la page consacrée aux restes
chinois |
||
|
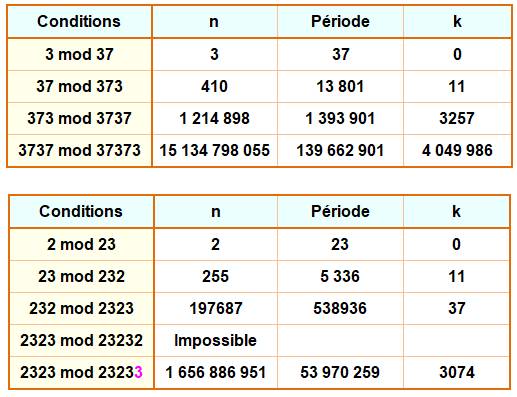
Cas de 45 et 454
Ici, la méthode ne se justifie pas, mais elle
permet de se re-familiariser avec la procédure. Simple ! Car deux contraintes seulement et de
plus avec un PGCD = 1. Cas de 45, 454 et 4545
Ici, on trouve bien les premiers paramètres en N,
en revanche, trouver les coefficients (91 et 3634) devient fastidieux sans outil.
Une recherche par programme s'impose.
On peut utiliser un tableur, mais avec beaucoup de persévérance. Cas de 45, 454, 4545 et 45454 Ici, la
méthode des restes chinois est extrêmement difficile. La recherche des
(grands) nombres dure des heures de calcul. C'est la solution incrémentale
qui nous sauve. |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |