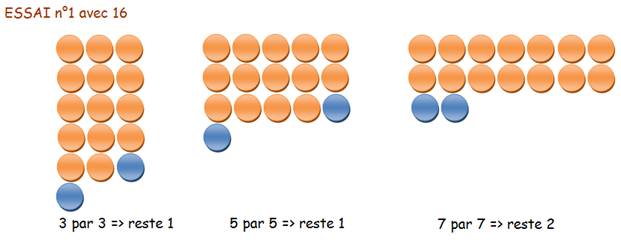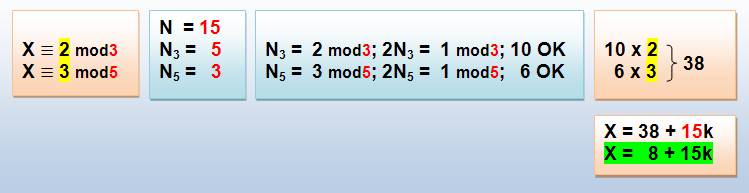NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 05/12/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

 

Arithmétique

 

 

Débutants

Opérations

MODULO

 

Glossaire

Nombres

Arithmétique et Théorie des nombres

 

>>> INDEX

Introduction

Théorie

Propriétés

Formulaire

Applications

Calculs

Carrés

Cubes

Jeux

Sun Zi

Mod 9, 10, 11

Carrés et Cubes

Parité

7 ^ 7 ^ 7

Log Modulaire

1110 = 32 mod 71

45, 454 …

Sommaire de cette page

>>> Problème de Sun Zi

>>> Essais

>>> Essais final

>>> Calculs (trois méthodes)

>>> Calcul général

>>> Procédure en un coup d'œil

>>> Calcul en modules non premiers entre eux

>>> Exemple 2, 3, 4, 5, 6, 7

>>> Exemple des 17 pirates

>>> Anglais

 

 

  

 

Les RESTES chinois

Problème de Sun Zi

 

Systèmes d'équations avec les congruences.

Approche imagée; méthodes de résolution; exemples classiques.

 

Exemple

Question

Comment retrouver le nombre 52 à partir des restes 1, 2 et 3 ?

Voir Nombre 52

 

 

Nombres "chinois"

Nombres tels que n mod 3 = 1 et n mod 5 = 2:

7, 22, 37, 52, 67, 82, 97…

Avec n mod 7 = 3, en plus:

52, 157, 262, 367, 472, 577, 682, 787, 892, 997…

Avec n mod 11 = 4, en plus:

367, 1522, 2677, 3832, 4987, 6142, 7297, 8452, 9607…

Avec n mod 13 = 5, en plus:

14227, 29242, 44257, 59272, 74287, 89302…

 

Théorème des restes chinois

Pour tous (a, b) et (m, n) – m et n premiers entre eux – il existe un nombre unique x tel que:

mn-1 est l'inverse de m modulo n.

Voir Application des formules de congruences

 

 

 

 

Énoncé

 

*      Sun Zi (ou Sun Tzu), le mathématicien chinois, (vers l’an 300) s’intéresse à des problèmes qui nécessitent un raisonnement impliquant les restes des divisons. Il cite par exemple:

 

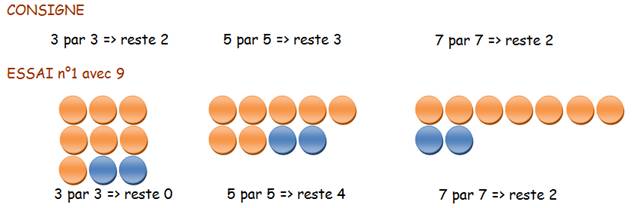
On ignore la quantité d’objets. Mais,

en les comptant 3 par 3, il en reste 2,

en les comptant 5 par 5, il en reste 3 et

en les comptant 7 par 7, il en reste 2.

Combien y a-t-il d'objets ?

 

*      La formulation exacte serait:

Combien l'armée de Han Xing comporte-t-elle de soldats si, rangés par 3 colonnes, il reste deux soldats, rangés par 5 colonnes, il reste trois soldats et, rangés par 7 colonnes, il reste deux soldats ?

 

Essais

 

Il faut au moins 7 objets pour les mettre en rang par 7. Le premier cas répondant à un des critères est 7 + 2 ; Ce nombre répond-il aussi aux deux autres critères (consigne).

 

 

La quantité 9 n’est pas suffisante. Elle satisfait le cas 7, mais par les cas 3 et 5.

L’essai suivant se fera avec 2 x 7 + 2 = 16.

 

La quantité 9 n’est pas suffisante. Elle satisfait le cas 7, mais par les cas 3 et 5.

 

 

 

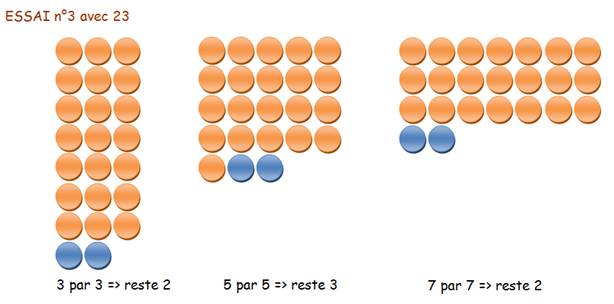
Essais final donnant le résultat escompté

 

L’essai suivant se fera avec 3 x 7 + 2 = 23.

 

 

Bingo ! 23, c’est la bonne solution.

Les solutions suivantes sont 128, 233, 338, 443, 548 …

Solution générique : 23 + 105k, en notant que 3 x 5 x 7 = 105.

 

En exigeant un reste égal à 2 pour les trois divisions
la solution serait 105k + 107.

 

 

 

Calculs (3 méthodes)

 

Équations

Mise en équation de l'énoncé et résolution classique.

 

3a + 2 = 5b + 3 = 7c + 2

3a = 7c

a = 7c / 3 et c est un multiple de 3

À ce stade, il faut faire des essais:

 

Si c = 3 => a = 7x3 /3 = 7

Et 5b + 3 = 7x3 + 2 => 5b = 20 => b = 4

Bilan: a = 7, b = 4, c= 3 et les termes de l'égalité valent 23.

 

Congruences – liste

On liste les valeurs successives des nombres modulo 3, puis 5, puis 7.

On cherche la concordance.

 

X mod 3 = 2 => X = {2, 5, 8, 11, 14, 17, 20, 23, 26 …}

X mod 5 = 3 => X = {  3,    8,    13,      18,     23,    28 …}

X mod 7 = 2 => X = {2,        9,        16,          23,       30 …}

 

Congruences – restes

On liste des nombres selon le module le plus grand (ici 7)

Puis, les restes de ces nombres selon les autres modulos.

On cherche les restes tels que demandés dans le problème.

 

X mod 7 = 2 => X = {2, 9, 16, 23, 30 …}

    mod 5                   {2, 4,    1,   3,   0 …}

    mod 3                   {2, 0,    1,   2,   0 …}

 

 

 

Calcul général

– Théorème des restes chinois

 

Il s'agit du problème général des restes chinois: on connaît les restes modulo divers nombres, il faut trouver le nombre en question.

 

Il n'est pas simple d'écrire les formules générales de calcul, mieux vaut dérouler un exemple. Le problème de SunZi est pris comme exemple.

 

Formellement, il s'agit de résoudre un système d'équations dans le monde des congruences. Le problème de Sun Zi s'écrit:

 

Écriture 1

Écriture 2

 

X mod 3 = 2

X mod 5 = 3

X mod 7 = 2

 

 

X  2 (mod 3)

X  3 (mod 5)

X  2 (mod 7)

 

 

Voici la procédure qui permet d'obtenir la solution dans le cas général:

 

1.   On calcule le produit des modules.

N = 3 x 5 x 7 = 105

2.   Pour chaque module, on calcule le produit des autres modules.

 

N3 = 5 x 7 = 35

N5 = 3 x 7 = 21

N7 = 3 x 5 = 15

 

3.   Pour chacun de ces nombres, on cherche un multiple dont le reste est 1 dans son modulo.
Avec 15 et 21, la solution est immédiate. Avec 35, il faut prendre deux fois cette valeur pour obtenir un reste égal à 1.

 

N7 = 15

N7    1 (mod 7) – OK 15 

 

N5 = 21

N5    1 (mod 5) – OK 21 

 

N3     = 35

N3      2 (mod 3) – mauvais 

2N3 = 70

2N3    1 (mod 3) – OK 70

 

4.   Somme des produits de ces nombres par les restes correspondants.
Le résultat est une solution.

X = 70 x 2 + 21 x 3 + 15 x 2

    = 233

5.   Solution minimale et
solution générique.

XMin = 233 – 2 x 105 = 23

XGén = 23 + 105k

 

 

Procédure en un coup d'œil  (avec deux restes)

Voir Exemple pratique (tour de magie)

 

 

 

Modules non-premiers entre eux

 

La procédure exposée ci-dessus fonctionne lorsque les modules sont premiers entre eux.

Si ce n'est pas le cas, on utilise les PGCD et PPCM. Mais, il n'y a pas toujours une solution:

 

Théorème

Si X  n1 (mod m1) et X  n2 (mod m2)

avec G = PGCD (m1, m2) et L = PPCM (m1, m2).

     Il existe une solution si et seulement si n1  n2 (mod G).

     La solution est unique modulo L.

 

Exemple:

X  3 (mod 4)

X  5 (mod 6)

 

1.   Module de la solution.

N = PPCM(4,6) = 2 x 2 x 3 = 12

2.   Changement de système pour obtenir des modules premiers entre eux.

Théorème: le reste est conservé pour les multiples du modulo.

 

X  3 (mod 4)

X  3 (mod 2) => X  1 (mod 2)

 

X  5 (mod 6)

X  5 (mod 2) => X  1 (mod 2)

X  5 (mod 3) => X  2 (mod 3)

 

3.   On conserve les modules tels que le produit donne bien le PPCM. En fait, on élimine les équations avec le PGCD comme module (Ici: 2).

 

X  3 (mod 4)

        qui contient bien X  1 (mod 2)

X  2 (mod 3)

 

4.   Calculs des Ni

 

N   = 12

N4 =    3

N3 =    4

 

5.   Recherche des restes à 1

N4     =    3

-1 x N4     1 (mod 4) – OK –3

(on peut aussi faire 3N4)

N3     =    4

N4       1 (mod 3) – OK 4

 

6.   Solutions

X = –3 x 3 + 4 x 2 = –1

X  = 11 + 12k

 

 

Autre exemple

 

Exemple:

X  1 (mod    4)

X  5 (mod  18)

 

1.   Module de la solution.

N = PPCM(4,18) = 36

2.   Changement de système

X  1 (mod 4)

X  1 (mod 2)

X  5 (mod 18)

X  5 (mod 2) => X  1 (mod 2)

X  5 (mod 9)

3.   Système équivalent

X  1 (mod 4)         

X  5 (mod 9)

4.   Calculs des Ni

N  = 36

N4 =   9

N9 =   4

5.   Recherche des restes à 1

N4     =    9

N4      1 (mod 4) – OK 1

N9     =    4

N9       4 (mod 9) – non

7N9     28 (mod 9)

            1 (mod 9) – OK  28

6.   Solutions

X = 9 x 1 + 28 x 5 = 149 

X = 5 + 36k

 

Résumé pour calcul express (cas d'un PGCD = 2)

 

 

Exemple 2, 3, 4, 5, 6, 7

 

X  1 (mod  2)       inclus dans 4

X  1 (mod  3)       OK

X  1 (mod  4)       OK

X  1 (mod  5)       OK

X  1 (mod  6)       inclus dans 2 en fait 4 et 3

X  0 (mod  7)       OK

 

1.   Coefficients

N  = 420

N3 = 140

N4 = 105

N5 =   84

N7 =   60

2.   Restes à 1

2N3 = 140    1 (mod 3)  – OK 140

  N4 = 105    1 (mod 4)   – OK 105

–N5 = –84    –1 (mod 5) – OK –84

2N7 = 120    1 (mod 7)   – OK 120

3.   Somme

X = 140 x 1 + 105 x 1 – 84 x 1 + 120 x 0 = 301

X = 301 + 420k

 

Résumé pour calcul express  (cas d'un PGCD = 1)

 

 

Exemple des 17 pirates

 

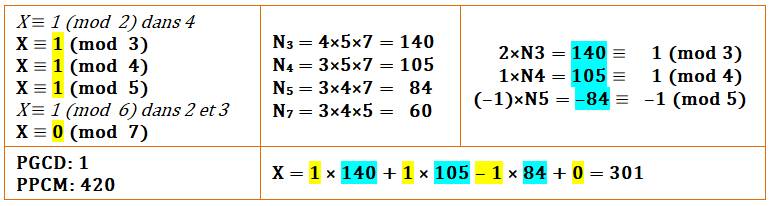
Dix-sept pirates possèdent un trésor en pièces d'or de même valeur. Partagé en parts égales, il reste trois pièces données au cuisinier. Six pirates sont tués, le partage laisserait 4 pièces pour le cuisinier. Après un naufrage, le trésor est intact et les six rescapés se partagent le trésor tout en laissant 5 pièces au cuisinier. Quelle est la valeur minimale du trésor?

 

X  3 (mod  17)

X  4 (mod  11)  

X  5 (mod    6)

 

4.   Coefficients

N   = 1 122

N17 =      66

N11 =    102

N  6  =    187

5.   Restes à 1

3N17 = 528    1 (mod 17)

4N17 = 408    1 (mod 11)

1N17 = 187    1 (mod   6)

6.   Somme

X = 528x3 + 408x4 + 187x5 = 4 151

X = 785 + 1 122k

Valeur minimale du trésor: 785 pièces d'or.

 

 

 

ENGLISH CORNER

 

Chinese Remainder Theorem.

The following problem was posed by Sun ZI: there are certain things whose number is unknown. Repeatedly divided by 3, the remainder is 2; by 5 the remainder is 3; and by 7 the remainder is 2. What will be the number?

 

The notion of modular arithmetic is related to that of the remainder in division. The operation of finding the remainder is sometimes referred to as the modulo operation.

 

 

 

 

 

 

Retour

*    Autre exemple de calcul

*    Approche

*    Équations avec les congruences

Voir

*    Jeux – Index

*    Équations

*    Divisibilité

*    Clé de divisibilité, une application de la théorie du modulo

*    La division

*    Exemple d'application du modulo en Codage RSA

*    Puzzle 45, 454, 4545,45454

Aussi

*    Bœufs d'Hélios

*    Calcul mental

*    Géométrie

*    Nombres Premiers

*    Nombres Rationnels

*    Preuve par 9 – Glossaire

*    Théorie des nombres

*    Variations sur les carrés

Site

*      Théorème des restes chinois – Wikipédia

*      A. Bogomolny, Chinese Remainder Theorem from Interactive Mathematics Miscellany and Puzzles

Cette page

http://villemin.gerard.free.fr/ThNbDemo/ModSunZi.htm

Référence de cette page

*      Les restes chinois – Problème de Sun Zi
http://villemin.gerard.free.fr/ThNbDemo/ModSunZi.htm