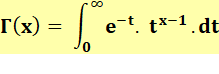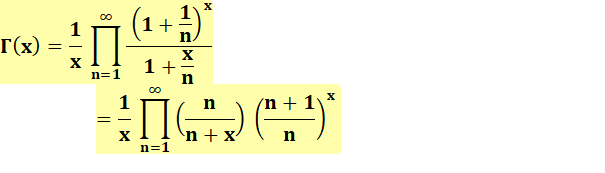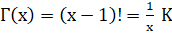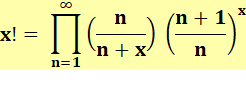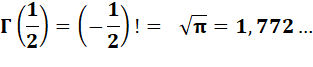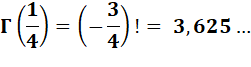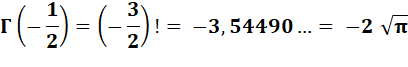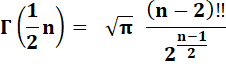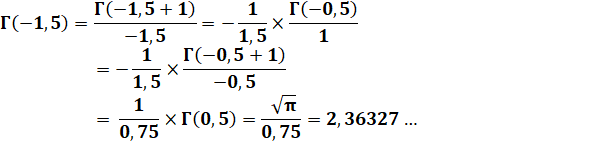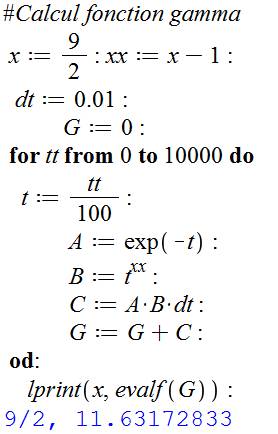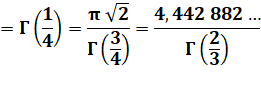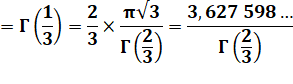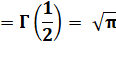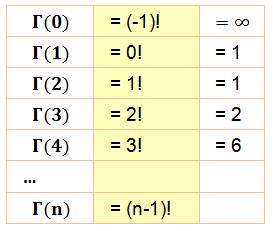
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER - Combinatoire
Débutants Dénombrement	FACTORIELLES			Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Introduction	Tronquées	Généralisées
		Alternée
	Niveau Terminale	Sommaire de cette page >>> Approche >>> Fonction gamma d'Euler >>> Calcul par itération >>> Calcul par intégration >>> Calcul par produits >>> Valeur typiques >>> Table de valeurs >>> Graphiques >>> Doublons

FACTORIELLES GÉNÉRALISÉES

Fonction gamma d'Euler

Fonction factorielle étendue aux nombres non-entiers

Ex: factorielle (1/2) = 1,77. Notée et lue gamma trois demis.

Important: avec des entiers, la fonction gamma de n est la factorielle de n – 1.

Note: on peut atteindre 7 avec deux 4 en faisant:

Voir Lettres grecques / Jeu du quatre 4

Approche
Nous connaissons les factorielles des nombres entiers. Que penser de la factorielle d'un nombre décimal, comme par exemple factorielle de 3,5. Par extension de la notion de factorielle, nous trouverions la valeur indiquée sur la courbe (11,63). Les mathématiciens (Euler le premier) ont introduit une fonction GAMMA () qui interpole les valeurs des factorielles entre les entiers. Ce prolongement n'est pas une fonction simple. Elle fait appel au calcul intégral. Ou autrement dit: à la somme infinie de quantités infinitésimales.	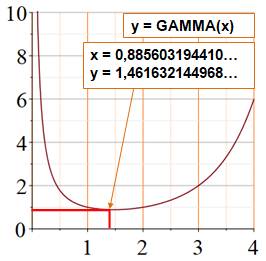Notez qu'il faut ajouter 1 en abscisse pour obtenir fonction GAMMA.

Point minimum

0,886 …

Valeur minimale de la fonction GAMMA (extension de la notion de factorielle aux nombres réels).

Voir Nombre 0,886… / A30171 / A30169

FONCTION GAMMA D'EULER

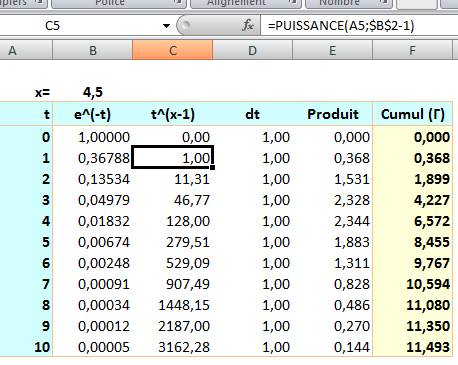
Nom Fonction gamma (GAMMA dans Maple) Fonction G d'Euler. Fonction eulérienne de première espèce Définition par intégrale et x sont des réels et x > 0 Lecture: gamma de x est égal à l'intégrale (sorte de sommes en quantité infinie) pour t variant de zéro à l'infini, du produit de l'exponentielle de moins t par t à la puissance x moins 1 et encore multiplié par dt (une quantité qui à la limite tend vers zéro, c'est cette petite quantité qui justifie le mot d'intégrale et non de sommes infinies). Définition par produits (en quantité) infinis Lecture: gamma de x est égal à un sur x multiplié par le produit infini d'une fraction dont le numérateur est égal à 1 plus 1 sur n le tout à la puissance x et le dénominateur est égal à 1 plus x sur n. Passage aux factorielles: (K étant toute la partie produit). En multipliant par x: x Soit la formulation en produit pour les factorielles: Merci à Mireille C. pour cette formulation Propriétés Si x est entier: (x) = (x – 1)! Ce qui explique le nom de factorielle généralisée. Gamma donne la factorielle décalée d'un cran. Si x est un réel: (x + 1) = x . (x) ou (x) = (x + 1) / x Il existe une généralisation avec les complexes. En pratique On trouve aussi bien la notation en GAMMA qu'en factorielle. Ainsi: Cas particulier des demis Où n!! est la factorielle des nombres impairs dite double factorielle. Par exemple: 5!! = 1 x 3 x 5 = 15.

Voir Constante gamma d'Euler / Symboles

Calcul par itération

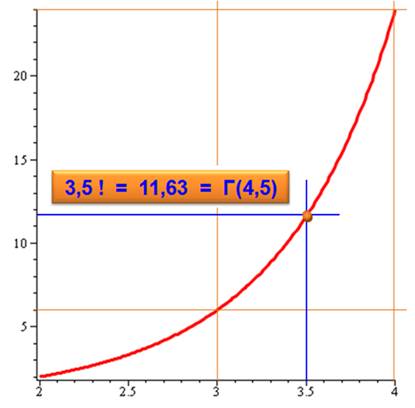
Entiers (5) = 4(4) = 4 . 3 (3) = 4 . 3 . 2 (2) = 4 . 3 . 2 . 1 (1) = 4 . 3 . 2 . 1 = 4! On retrouve bien la relation entre la fonction gamma et les factorielles des entiers. Fractionnaires (4,5) = 3,5 (3,5) = 3,5 x 2,5 (2,5) = 3,5 x 2,5 x 1,5 (1,5) = 3,5 x 2,5 x 1,5 x 0,5 (0,5) = 6,5625 x 1,77245 = 11,6317… >>> Alternative En prenant la formule spécifique des demis, la quantité de demis n = 9 et le coefficient de racine de Pi est égal à : (9 – 2) !! / 2^4 = 1 x 3 x 5 x 7 / 16 = 105 / 16 = 6,5625. Négatifs

Principe du calcul avec la définition par intégrale
Voici une approche du calcul intégral, réalisable sur tableur ou mieux par programmation. Ci-contre exemple de calcul avec tableur (Excel). le pas de calcul (dt) est fixé à 1. On approchera de plus près la valeur réelle (11,63) en choisissant un pas plus petit; il faudra alors adapter la valeur de t. Par exemple avec dt = 0,1 la variable t passera de 0 à 0,1 puis 0,2 jusqu'à atteindre 10 ou plus. la valeur finale proposée ici pour t = 10 est arbitraire. La théorie voudrait que le calcul soit prolongé à l'infini. En pratique, plus la quantité de calcul est grande et plus on se rapproche de la valeur réelle.
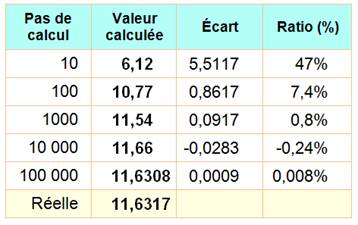
Avec Maple, voici un programme tout simple qui permettra de choisir le pas de calcul à loisir et laisser faire l'ordinateur. Ici, le pas de calcul est dt = 0,01 et la quantité de pas est tt = 10 000. Le calcul est effectué pas à pas avec A, B et C les calculs intermédiaires et G qui est le cumul de C. La valeur donnée par la fonction GAMMA de Maple est: = 11,631 728 396 6…		Initialisation Boucle de calcul Impression

Principe du calcul avec la définition par produits
La mise en musique (tableur ou programmation) n'est pas bien difficile. Par contre, la convergence est très lente. La difficulté, sans connaître la valeur finale, c'est de savoir quand s'arrêter!	Exemple pour

Quelques valeurs typiques (100 décimales)
	= 3,6256099082 2190831193 0685155867 6720029951 6768288006 5467433377 9995699192 4353872912 1618360136 7233843003…
	= 2,6789385347 0774763365 5692940974 6776441286 8937795730 1100950428 3275904176 1016774381 9540982889 0411887894…
	= 1,7724538509 0551602729 8167483341 1451827975 4945612238 7128213807 7898529112 8459103218 1374950656 7385446654…
	= 1,3541179394 2640041694 5288028154 5137855193 2726605679 3698394022 4679637829 6540174254 1675834147 9529729111…
	= 1,2254167024 6517764512 9098303362 8905268512 3924810807 0611230118 9382898228 8842679835 7237172376 2149150665 …

3,625 609 ...	En 2018, cette constante est connue avec 50 milliards de décimales – Alexander Yee Voir Nombre 3,6256… Les nombres , , et (1/4) sont indépendants . Démonstration 1995
2,678 938 ...	Nombre transcendant . Indépendance algébrique: il n'existe pas de polynôme à coefficients non nuls liant ces deux nombres – (1/3) et ) – et prenant la valeur nulle. Choodnovsky Voir Nombre 2,678…
1, 772 453 …	Nombre transcendant. Voir Nombre 1,772…

Voir Pi pannumérique avec fonction gamma

TABLE de valeurs des fractions de 1 à 10 pour N et pour D

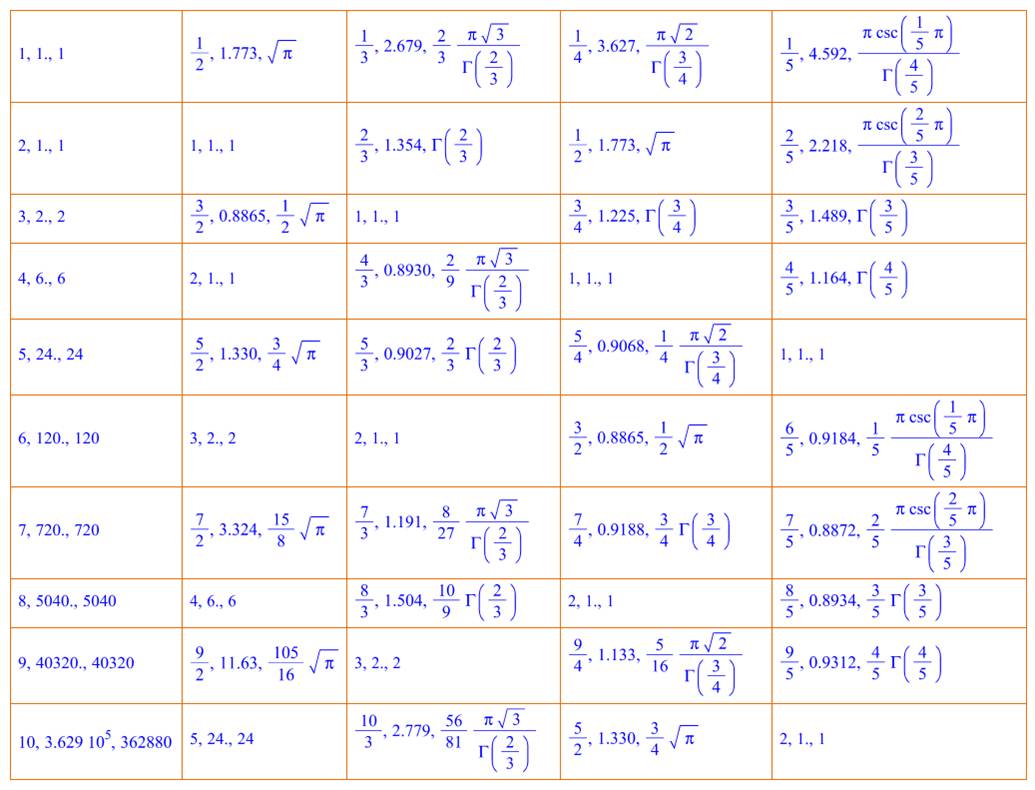
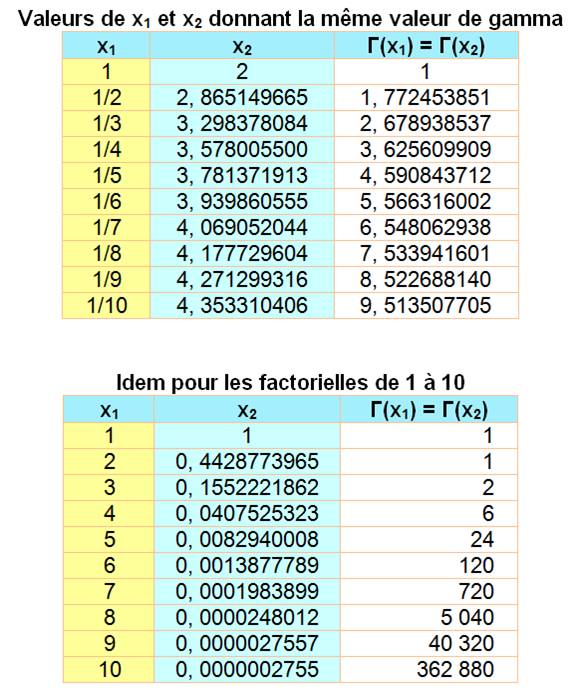
Lecture: Trois valeurs ; sa valeur numérique avec 4 chiffres significatifs, les 0 finaux sont éliminés; et, enfin, son expression en fonction d'autres valeurs Ex: qui s'exprime par racine de Pi. La fonction csc est la cosécante; c'est simplement l'inverse du sinus. On aurait pu mettre le sinus de la même valeur au dénominateur Note: la première colonne présente les fractions ayant 1 pour dénominateur. Autrement-dit, les nombres entiers de 1 à 10. La fonction gamma donne la valeur de la factorielle classique, décalée d'un cran.

Visualisation graphique
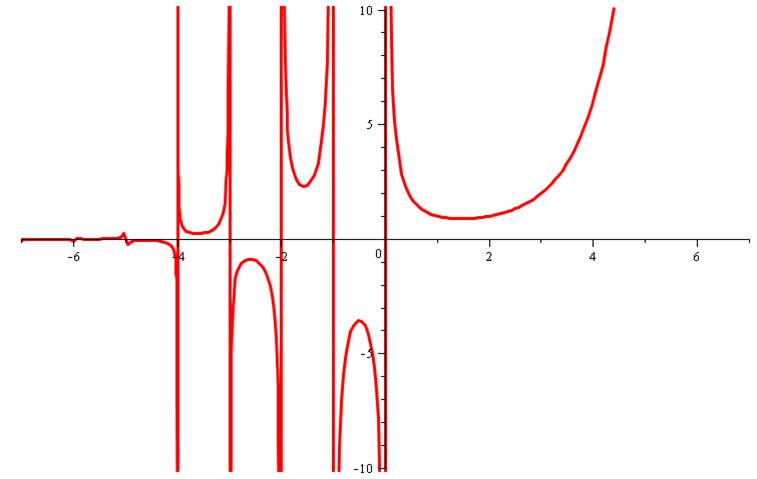
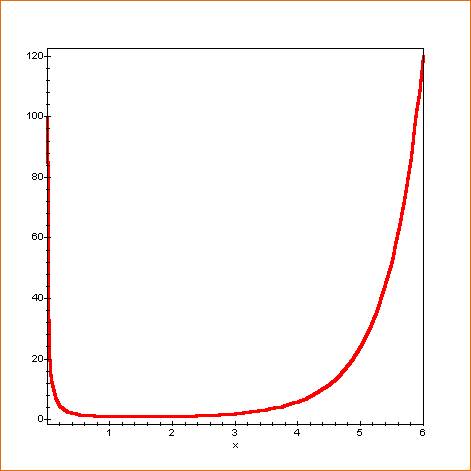
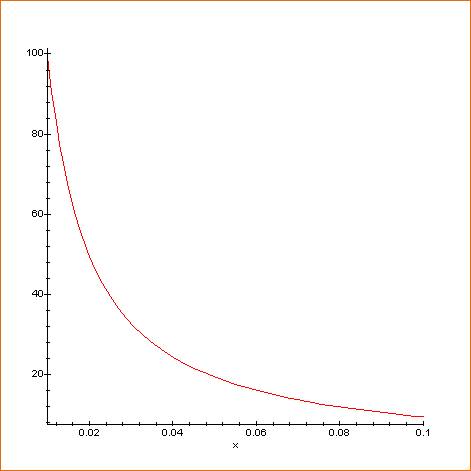
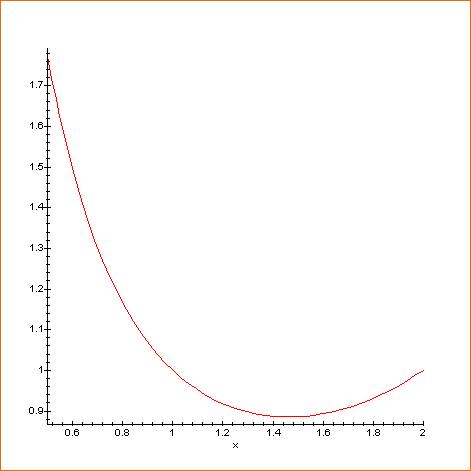
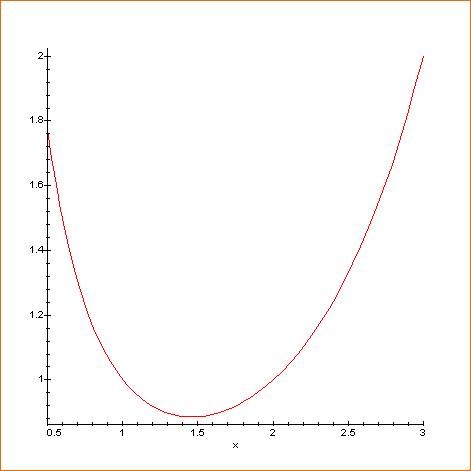
Courbe pour x de – 6 à + 6, montrant la non-définition de la fonction pour les valeurs entières négatives Courbe pour x de 0,001 à 6 ZOOM Courbe pour x de 0,01 à 0,1 Courbe pour x de 0,5 à 2 Courbe pour x de 0,5 à 3 Notez que pour x =1 et x = 2, même valeur de gamma = 1 D'une manière générale: même valeur pour deux abscisses.

DOUBLONS
Attention ( x ) = (x – 1)! Les valeurs des factorielles sont décalées d'un cran. ( 4 ) = 3! = 6

Suite	· Sous-factorielles · Factorielle tronquée généralisée (Nombres de Stirling) · Formule du volume de l'hypersphère
Voir	· Coefficient du binôme · Constante "e" · Constante "pi" · Constantes · Euler – Biographie et Index · Factorielles divisées · Jeux de chiffres · Loto · n! + 1 = a² (Brocard) · Programmation du calcul des factorielles · Théorie des nombres – Index
DicoNombre	· Nombre 222 · Nombre 145
Sites	· Calculateur de Gamma (Gamma function finder)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/Factgene.htm