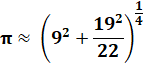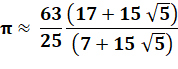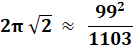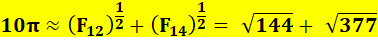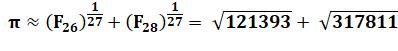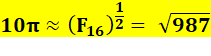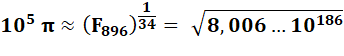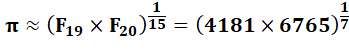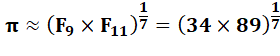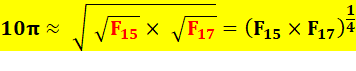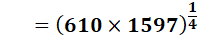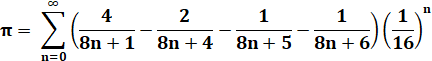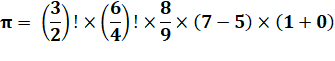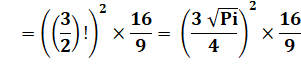|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
![]()
|
VALEUR
DE Suite |
Anglais: Pi value to
100 decimal places
|
|
|
|
|
|
=
3,14159265258266 |
1,24666375151019 =
3,14159265380568 |
= 9801 / 1103 = 8,885766092 |
|
|
écart = 0,100 10-8 |
écart = 0,216 10-9 |
écart
= 0,216 10-6 |
|
|
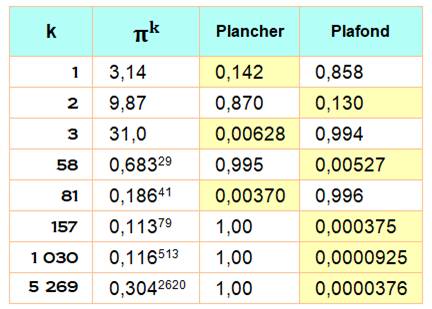
Quelles
sont les puissances k de Pi qui se rapprochent le plus d'un entier ? Valeur
de k record en jaune.
Exemples:
Pi3 =31,006277 … proche du nombre 31 à 0,006277 … près. |
|
Pi en base 2 = 11, 0010 0100 0011 1111 0110 1010 1000 1000 1000 0101 1010 0011 0000 1000
1101 0011 0001 0011 0001 1001 1000 1010 0010
1110 00 … (100 chiffres) Pi en virgule flottante = 0 10000000 10010010000111111011011 |
|
Voir Pi en
base 4 et humour
|
|
Voir Formules
d'Euler / Fonction zêta |
||
|
6
/ |
|
||
|
( |
|
||
Suite en Formules
|
|
3,140968877… |
|
|
|
|
3,142191833… |
|
|
|
|
3,141640783… |
|
|
|
|
3,141577387… |
|
|
|
|
3,141598280… |
Due
à Michele Fanelli |
|
|
|
2,71828180861191… |
Due
à Castellanos |
|
|
|
||
|
On cherche une approximation
de Pi avec la racine énième des nombres de Fibonacci, ou encore avec
somme ou produit de deux nombres de Fibonacci. |
||
|
|
= 31,41648784… EPi = 0,0000561… Approximation
due à Joseph-Claude Barbier – 2017 |
|
|
Coquetterie avec les nombres 26, 27 et 28. |
= 3,141540909… EPi = 0,0000517… |
|
|
Avec Fn + Fn+2 : pas mieux
jusqu'à F1000 et jusqu'à racine 1/100 |
||
|
Avec Fn + Fn+1 : même ordre
de grandeur de l'écart pour racine 44e et 91e. Peu
d'intérêt. |
||
|
|
= 31,41655614… EPi = 0,0000629… |
|
|
|
= 314166,6054… EPi = 0,0000734… |
|
|
Avec Fn seul: pas mieux jusqu'à F1000
et jusqu'à racine 1/100 |
||
|
|
= 3,138844959… EPi = 0,00274… |
|
|
|
= 3,142439963… EPi = 0,000847… |
|
|
Rappel liant les deux
approximations ci-dessus notées en jaune: F16 2 = F15 x F17 – 1 987² = 974 169 = 610 x 1597 – 1
|
= 31,41656421… EPi = 0,0000637… Approximation due à
Joseph-Claude Barbier – 2017 |
|
|
Avec Fn x Fn+1 (successifs) Avec Fn x Fn+2 (les pairs
ou les impairs) |
Pas mieux jusqu'à F1000 et jusqu'à racine 1/100 |
|
|
Ces approximations sont le fruit du hasard des
nombres. On aurait pu chercher une explication du côté du rapport entre nombres de Fibonacci
qui se rapprochent du nombre d'or pour les grands
nombres:
et notre produit:
Cependant, rien de particulier avec sa racine
énième. en rapport avec Pi. |
||
Voir Nombre
987
|
|
|
|
Algorithme de Bailey-Borwein-Plouffe – 1995
David Bailey, Peter Borweinet et Simon
Plouffe ont calculé les chiffres de Pi
au 10 milliardième rang, mais en
hexadécimal (en fait base 2 ou base 2n).
Travaux réalisés sur ordinateur en utilisant un langage formel La formule utilisée permet de calculer un
chiffre de rang quelconque sans connaître les précédents. Personne ne
supposait qu'il était possible de construire de tels algorithmes.
On ne connaît pas l'algorithme permettant de faire la même chose en décimal. Formule
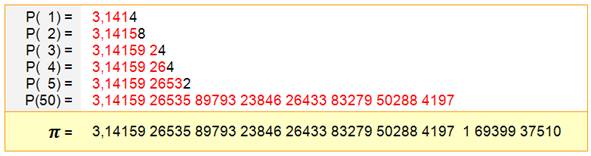
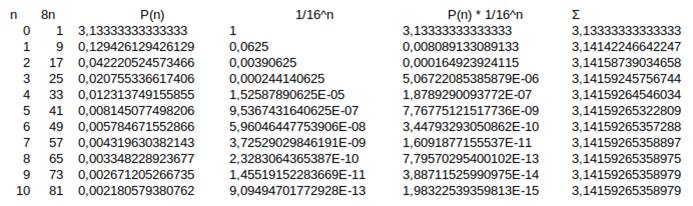
Ce que donne cette
formule
Détail des calculs
Merci à Laurent Touchard |
|
Voir Limite
de calcul des décimales de Pi
Point de Feynman: Pi un nombre presque entier?
|
Richard
Feynman
(1918-1988) aimait réciter les décimales de Pi en s'arrêtant à cette séquence
de six 9 de suite tout en disant etcétéra. Le premier de ces 9 se trouve à la
762e décimale. 3. 1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799
6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999… Suite pour atteindre 1000 décimales
4999999837
2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035
2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904
2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787
6611195909 2164201989 |
Voir Table
des décimales de Pi / Nombres
presque-entiers / Nombre
999 999
|
En
2004, Daniel Tammet (1979-) récite 22
514 décimales de Pi en 5 heures, 9 minutes et 24 secondes, soit 0,8 s par
chiffre. Il avait mis trois mois à les apprendre. |
|
|
||
|
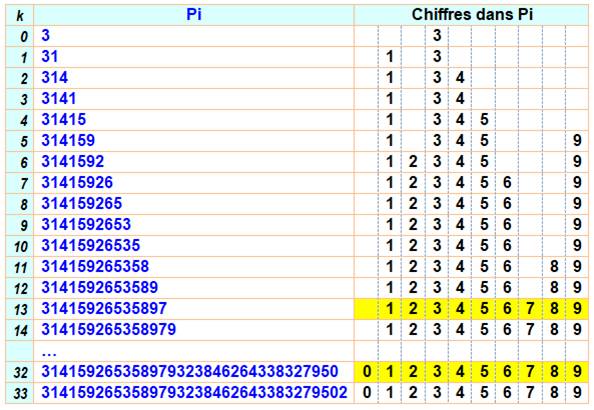
Combien faut-il de décimales
pour que Pi contiennent tous les chiffres de 1 à 9 ? Réponse: 13 Et pour tous les chiffres de
0 à 9 ? Réponse: 32. |
|
|
Formule pannumérique de Plouffe
et Ed Pegg Jr, indépendamment
|
|
= 3,1415926539165017461… Écart avec Pi = 3,26 10-10 Note: le 0 peut être
introduit comme exposant du 1 ou simplement ajouté à la formule. |
Anglais: pandigital approximation to Pi
|
Expressions pannumériques de
Pi |
Position
des décimales 3,8415926
– 0,7 = 3,1415926 Toutes
les décimales sont exactes. Écart: 5,4 10-8 Expression
algébrique approchée
22 décimales pour un écart: -1,1 10-18 Formule due à G. W. Barbosa Expression
algébrique exacte
Voir Fonction
gamma (factorielle de fractions) |
Voir Pannumérique / Carrés et cubes pannumériques
/ Puissances de 2 pannumériques
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La constante Pi et ses décimales sont
parfois utilisées comme objet de questions dans des olympiades ou des
rallyes. Ce tableau propose une source d'inspiration
ou de recherche de solutions. Il donne la différence entre les décimales
(Pi1) et des groupes de décimales (Pi2 à Pi5) considérés comme des nombres.
Exemples de lecture
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Jeux et énigmes – Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiValeu1.htm
|
![]()