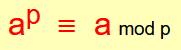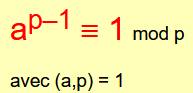NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/03/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
Index général >>> INDEX	Index divisibilité	Divisibilité par 30 et 31	Autres
		Sommaire de cette page >>> Divisibilité de n^5 – n >>> Divisibilité de n^5 – n, avec n impair >>> Exemples >>> Divisibilité par 31

DIVISIBILITÉ par 30 et 31

Critères de divisibilité et formes polynomiales.

Développement (pour information)

n⁵ – n = n (n⁴ – 1) = n (n² – 1) (n² + 1) = n (n – 1) (n + 1) (n² + 1)

n⁵ – n = (n – 2) (n – 1) n (n + 1) (n + 2) + 5 (n – 1) n (n + 1)

Voir Identités remarquables

Divisibilité de n^5 - n
Remarquons ce que vaut cette expression en fonction du produit de cinq nombres consécutifs.	(n – 2) (n – 1) n (n + 1) (n + 2) = (n^2 – 4) (n^2 –1) n = (n^4 – 4n^2 – n^2 + 4) n = n^5 – 5n^3 + 4n = n^5 – n – 5n^3 + 5n = n^5 – n – 5n (n^2 – 1)
Alors considérons cette égalité de la manière suivante. Elle est exprimée par la somme de deux termes: L'un factorisant cinq nombres consécutifs; L'autre factorisant trois nombres consécutifs.	n^5 – n = (n – 2) (n – 1) n (n + 1) (n + 2) + 5n (n^2 – 1) = (n – 2) (n – 1) n (n + 1) (n + 2) + 5 (n – 1) n (n + 1)
Or le premier terme est le produit de cinq nombres consécutifs. Il est divisible par 120.	1 x 2 x 3 x 4 x 5 = 120 120 | (n – 2) (n – 1) n (n + 1) (n + 2)
Le deuxième terme est le produit de 5 et de trois nombres consécutifs; il est divisible par 6 et par le facteur 5 du produit.	5 x 1 x 2 x 3 = 30 30 | 5 (n – 1) n (n + 1)
La somme des deux termes est divisible par le PGCD de ces deux diviseurs.	(120,30) = 30 30 | (n^5 – n)

Voir Divisibilité par 30 (Terminale)

Autre démonstration avec le Petit théorème de Fermat (PTF)

PTF: ou

Exemples	3^5 – 3 = 240 3^4 – 4 = 1020
Multiple de 2
si n est pair, n^5 l'est	n^5 – n est pair
si n est impair, n^5 l'est	n^5 – n est pair
Multiple de 3
si n est multiple de 3, n^5 l'est	n^5 – n est multiple de 3
sinon en modulo 3 (PTFdroite)	n^5 – n = n² · n² · n – n ≡ 1 · 1 · n – n = 0
Multiple de 5 (PTFgauche)	n^5 – n ≡ 0 mod 5
Multiple de 2, 3 et 5	Multiple de 30.

Divisibilité de n^5 – n, avec n impair
Dans le cas où n est impair, le deuxième terme de l'adition possède une propriété supplémentaire. Dans ce cas, le produit des trois nombres consécutifs est divisible par 24 Et multipliée par 5, ce deuxième terme est globalement divisible par 5 x 24 = 120	24 | (n – 1) n (n + 1) pour n impair 120 | 5 (n – 1) n (n + 1) pour n impair
Bilan: les deux termes sont divisibles par 120 La somme est divisible par 120, pour n impair.	120 | (n – 2) (n – 1) n (n + 1) (n + 2) 120 | 5 (n – 1) n (n + 1) pour n impair 120 | (n^5 – n) pour n impair
De plus, ces deux termes sont pairs (car divisible par 120, a fortiori par 2), leur somme est divisible par 2 et l'expression par 2 x 120 = 240	240 | (n^5 – n) pour n impair
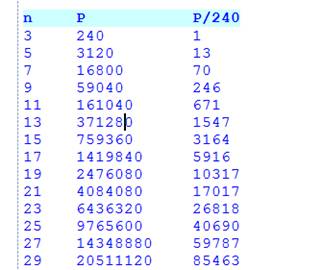
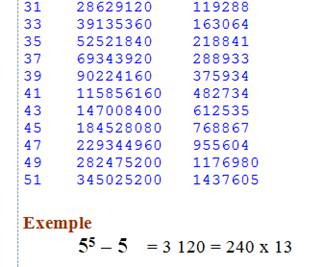
Note Exemple avec n = 3 le produit des 5 consécutifs 1 x 2 x 3 x 4 x 5 = 120 le produit des 3 consécutifs par 5 donne 1 x 2 x 3 x 4 x 5 = 120 La somme 120 + 120 = 240 ajoute une divisibilité par 2

Exemples

Divisibilité par 31
Affirmation 31 (2^5n - 1) Démonstration 2^5n – 1 = (2^5)^n – 1 = (2^5 – 1) (2^5(n-1) + 2^5(n-2) + … 2^5 + 1 ) = 31 . k

Voir Divisibilités de 2^{n -1}

Retour	Divisibilité par 24
Suite	Divisibilité par 36 Divisibilité par 37
Voir	Diviseurs Divisibilité – Index Divisibilité et Fermat Divisibilité par nombre – Récapitulatif
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi30.htm