|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
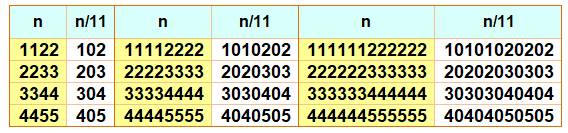
NOMBRES
UNIFORMES double ou REPDIGITS
double ou Bi-Repdigits Nombre de la forme aa…aabb…bb. Leurs propriétés de divisibilité. Objet d'énigmes: trouvez tous ces
nombres divisibles par 45. Exemple
6 facteurs et 64 diviseurs. Si
on divise de tels nombres par k de 1 à n, on trouve plusieurs tels nombres
divisibles plusieurs fois jusqu'à 41. Celui-ci n'est divisible qu'une seule
fois par 42. |
|
Exemples
est
un nombre dont les chiffres sont en a et b comme 22225555. Par
la suite, on simplifie la notation en omettant le surlignement. Avec
ce nombre, on a: a+a+b+b = a+a+b+b
qui indique que le nombre est divisible
par 11. Tous les nombres en
aa…abb…b avec une quantité paire de chiffres sont divisibles par 11. Par exemple:
88889999 = 11 x 8080909 |
|
|
||
|
Énigme Quelles
sont les valeurs de a et b telles que N = aaaabbbb soit divisible par 45? Une des solutions
|
Solution Notons que a et b sont des chiffres: a < 10 et b < 10. Si N est divisible par 45, il l'est par 5 et par 9. Divisible par 5,
alors b = 0 ou 5. Divisible par 9,
alors 4a + 4b = 9k Si b = 0, alors 4a = 9k et a = 9 (a < 10) et N = 99990000. Si a = 0 et b = 0, alors N = 00000000, trivial Si a = 0 et b = 5, alors 4a + 4x5 = 9k ou 4 (p + 5) = 9k alors p + 5 = 9 et p = 4 N = 44445555 Notez
que ces deux
nombres sont également divisibles par 11, soit au bilan par 11 x 45 = 495. |
|
|
Bilan |
Parmi tous les nombres en aaaabbbb, seuls 44445555 et 99990000 sont
divisibles par 45. |
|
|
Nombres 44445555 et
99990000 |
44 445 555 = 32
x 5 x 7 x 11 x 101x 127 99 990 000 = 24 x 32 x 52 x 11 x 101 |
|
|
Forme générique |
44 445 555 = 1111 (1000 x 4 +
5) 99 990 000 = 1111 (1000 x 9 +
0) |
|
|
Nombre 1111 (repdigit) |
1 111 = 11 x 101 |
|
Anglais: The eight-digit number ppppqqqq, where p and q are digits, is a multiple of 45. What are
the numbers?
|
Cette
énigme avec une divisibilité par 45 est assez classique. Elle est bien
choisie car:
Prenons
la divisibilité par 99. Le nombre est donc divisible par 11. Peu intéressant,
car tous ces nombres le sont. Il est divisible par 9. Alors il suffit que a +
b = 9 et nous avons ainsi 10 nombres comme 11118888, 22227777, etc. |
|
|
||
|
2-bi-repdigits |
N = aabb = 11 (100a + b) Tous divisibles par 11. Il y en à 90 (9 possibilités pour a et 10 pour b) Record de divisibilité avec 5 544 qui est divisible par 27 nombres. 5 544 = 23 x 32 x 7 x 11= 504 x 11 |
|
|
3-bi-repdigits |
N = aaabbb = 111 (1000a + b) Tous divisibles par 3, 37 et 111. Il y en à 90. Record de divisibilité avec 888 888 qui est divisible par 29 nombres. 888 888 = 23 x 3 x 7 x 11 x 13 x 37 = 8008 x
111. |
|
|
4-bi-repdigits |
N = aaaabbbb = 1 111 (10 000a + b) Tous divisibles par 11, 101 et 1 111. Il y en à 90. Record de divisibilité avec 11118888 qui est divisible par 18 nombres.
11 118 888 = 23 x 32 x 11 x 101 x 137 = 10 008 x
1111. Parmi tous ces nombres, aucun n'est divisible par 49, 51, 53, 67, 68,
78, 84, 89, 91, 92, 93, 95, 97, 98, 102 … Parmi tous ces nombres, certains ne sont divisibles qu'une seule fois par un nombre donné: 99996666/42, 55552222/ 46, 55554444/54, 77776666/58, 33338888/62,
44445555/63, 77775555/65, 11115555/69, 7777000/70, 77776666/71, 77774444/74,
55558888/76, 55557777/79, 22227777/81, 33335555/85, 77774444/86, 11115555/87,
99990000/90, 55558888/94, 66660000/96, 66668888/104 … D'autres deux fois seulement comme 31, 34, 35, 37, 38, 39, 41, 43 ou encore 45, objet de l'énigme. |
|
|
5-bi-repdigits |
N = aaaaabbbbb = 11 111 (100 000a + b) Tous divisibles par 41, 271 et 11 111. Il y en à 90. Record de divisibilité avec 5555544444 qui est divisible par 20
nombres. 5 555 544 444 = 23 x 32 x 17 x 19 x 41 x 43 x
271 = 500 004 x 1111. |
|
|
|
||
|
Exercice
avec un tableur: trouver les nombres de la forme N = aaaabbbb divisibles par
un nombre k donné. |
Pour créer tous les nombres de cette forme, on utilise la forme
générique: N = aaaabbbb =
1111(10 000a + b) |
|
|
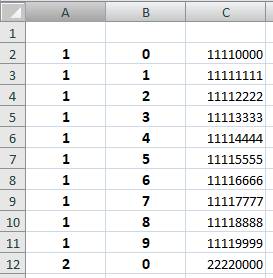
La
formule est entrée dans la troisième colonne : Alors
qu'en colonnes A et B on déroule les valeurs de a et b En A12 : =A2+1 et en B12: =B2
Comme d'habitude, on sélectionne A12 et B12 et on tire la poignée en bas à droite pour renouveler les formules jusqu'à atteindre 99. |
|
|
|
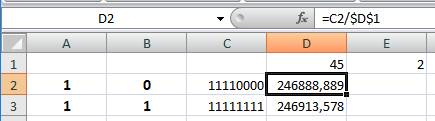
Le nombre
k (ici 45) est placé en D1. En D2, on
divise le nombre N par k: =C2/$D$1, le symbole S indique une cellule fixe: c'est toujours cette valeur
qui est à prendre en compte La
formule est prolongée jusqu'en bas. En E2,
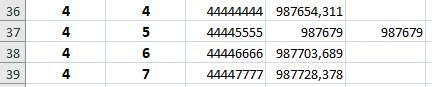
cherche les valeurs entières de la division comme celle trouvée en D37.
Formule: =SI(D2-PLANCHER(D2;1)=0; PLANCHER(D2;1);" ") En E1, on
compte la quantité de valeurs entières sur toute la colonne: =NB(E2:E91) |
…
…
Les deux seuls nombres en aaaabbbb divisibles par 45 sont indiqués dans
ce tableau. |
|
Voir Programmation – Tableur – IndSex
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Formes/aaaDivis/BiRpDgit.htm |
![]()